ÉVALUATION – 10 points – Durée 1h – calculatrice autorisée
Sujet 2024 n°SPEPHCH108 et n°SPEPHCH116
Télécharger l’exercice en PDF :
Le frottement de l’air sur une voiture ou de l’eau sur une coque de bateau sont deux situations parmi d’autres qui illustrent les frottements fluides. De façon générale, lorsqu’un objet se déplace dans un fluide, il subit de la part de celui-ci une force de frottement dont les caractéristiques dépendent de la vitesse de l’objet par rapport au fluide, de sa forme et des propriétés du fluide. Cette force de frottement fluide s’oppose au mouvement.
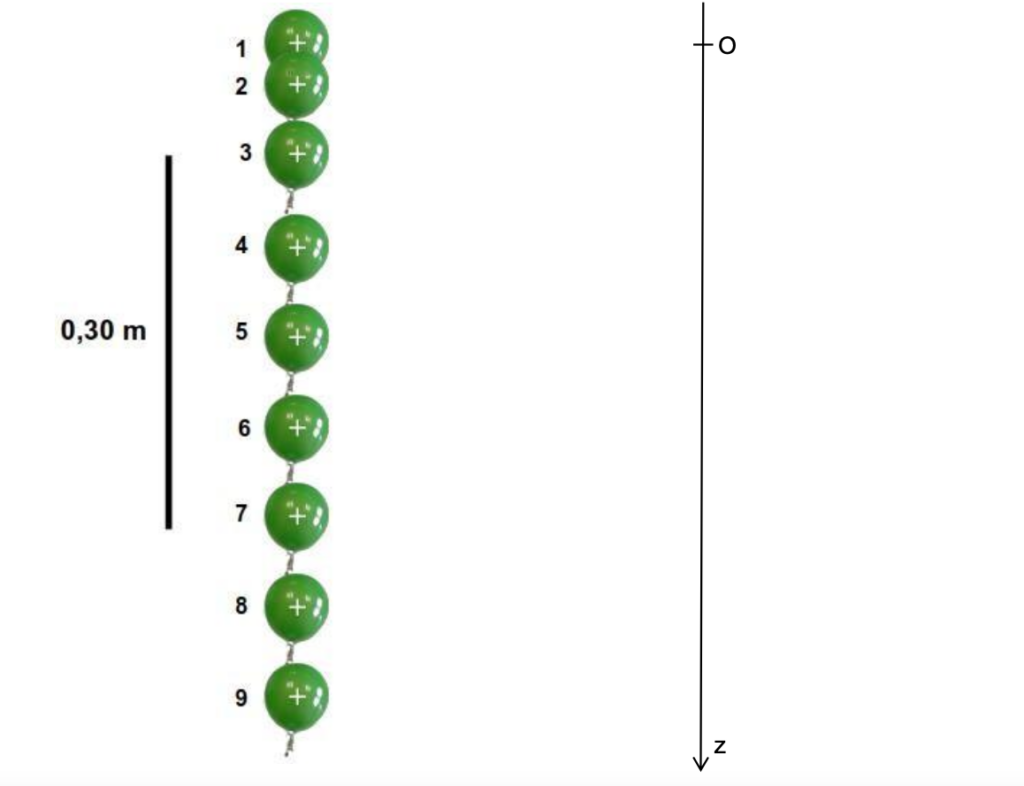
Pour étudier cette force de frottement au laboratoire, on relève toutes les 0,12 s la position du centre M d’un ballon de baudruche lâché sans vitesse initiale. La chronophotographie obtenue est représentée ci-après.
Données :
- intensité du champ de pesanteur terrestre : g = 9,81 m.s-2 ;
- tout corps immergé dans un fluide subit de la part de celui-ci une action modélisée par une force $\overrightarrow{F_A}$ appelée poussée d’Archimède verticale, dirigée de bas en haut ;
- la force de frottement $\overrightarrow{f}$ exercée par l’air sur le ballon de baudruche est opposée au mouvement de celui-ci ;
- dans cet exercice, on étudie le mouvement du centre de masse M du ballon de baudruche de masse m = 6,05 g ;
- valeur de la poussée d’Archimède subie par le ballon : FA = 1,2×10-2 N.
Le référentiel d’étude est le référentiel terrestre supposé galiléen.
1. Mouvement du ballon de baudruche
1.1. À partir de la chronophotographie représentée ci-avant, montrer que le mouvement du point M est constitué de deux phases que l’on décrira avec les termes scientifiques appropriés.
Le mouvement du point M est constitué de deux phases :
Seconde phase entre les points 5 et 9. Le ballon à une trajectoire en ligne droite, la distance entre les points est constante au cours de la chute : le mouvement est rectiligne uniforme.
Première phase entre les points 1 et 5. Le ballon à une trajectoire en ligne droite, la distance entre les points augmente au cours de la chute : le mouvement est rectiligne accéléré.

1.2. Montrer que, lors de la seconde phase du mouvement, la valeur v de la vitesse du point M est égale à 0,61 m.s-1.
Calculons la vitesse au point 6 :
| Schéma | Réel |
| 6,7 cm | 0,30 m |
| 1,55 cm | M6M7 |
$v_6 = 0{,}58 \ \text{m}\cdot\text{s}^{-1}$
\[ M_6 M_7 = \frac{1,55 \times 0,30}{6,7} \]
\[ M_6 M_7 = 0,069 \, \text{m} \]
\[ v_6 = \frac{M_6 M_7}{\Delta t} \]
\[ v_6 = \frac{0,069}{0,12} \]
\[ v_6 = 0,58 \, \text{m.s}^{-1} \]
2. Forces exercées sur le ballon de baudruche
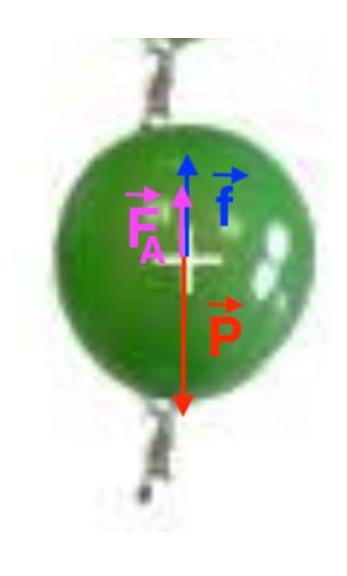
2.1. Représenter sans souci d’échelle les forces exercées sur le ballon de baudruche lors de son mouvement.
Les forces s’exerçant sur le ballon de baudruche sont :
– Le poids \(\overrightarrow{P}\)
– La poussée d’Archimède \(\overrightarrow{F_A}\)
– Les forces de frottement \(\overrightarrow{f}\)
2.2. Calculer la valeur du poids du ballon de baudruche.
\[ P = m \times g \]
\[ P = 6{,}05 \times 10^{-3} \times 9{,}81 \]
\[ P = 5{,}94 \times 10^{-2} \, \text{N} \]
2.3. Les données du pointage peuvent être traitées à partir d’un programme en langage Python. Un extrait de ce programme est reproduit ci-après :
28 DVz=[ ]
29 for i in range(len(Vz)-2):
30 DVz=DVz+[(Vz[i+1]-Vz[i])]
31 produit = [ ]
32 for i in range(len(DVz)):
33 produit = produit+[0.05*DVz[i]]
34 for i in range(len(t)-3):
36 print(‘Au point’,i+1,’m*delta v / delta t vaut’, round(produit,2),\’ kg.m/s2’)
2.3.1. Repérer la ligne permettant le calcul de l’expression $m \times \frac{\Delta v}{\Delta t}$ . Quel est l’intérêt de ce calcul pour déterminer la valeur de la force $\overrightarrow{f}$ ?
La ligne permettant le calcul de l’expression \(\frac{m \times \Delta v}{\Delta t}\) est la 33 produit = produit+[0.05*DVz[i]]
Ce produit nous permet de connaître la somme des forces et, connaissant \(\overrightarrow{P}\) et \(\overrightarrow{F_A}\), d’en déduire la valeur de la force \(\overrightarrow{f}\).
2.3.2. Retrouver la valeur numérique « 0.05 » qui intervient à la ligne 33.
\[ \mathrm{ \frac{m \times \Delta v}{\Delta t} = m \times \frac{1}{\Delta t} \times \Delta v}\]
Calculons \( m \times \frac{1}{\Delta t} \) :
\[ \mathrm{ m \times \frac{1}{\Delta t} = 6{,}05 \times 10^{-3} \times \frac{1}{0{,}12}}\]
\[ \mathrm{ m \times \frac{1}{\Delta t} = 0{,}050}\]
La valeur numérique « 0,05 » qui intervient à la ligne 33 est le résultat du calcul \( m \times \frac{1}{\Delta t} \).
2.4. On s’intéresse au mouvement du point M entre les positions n°6 et n°9.
2.4.1. Que peut-on dire de la somme des forces s’exerçant sur le ballon de baudruche entre ces deux positions ? Justifier.
Entre les points 6 et 9. Le ballon à une trajectoire en ligne droite, la distance entre les points est constante au cours de la chute : le mouvement est rectiligne uniforme.
D’après la première loi de Newton, lorsqu’un système est en mouvement est rectiligne uniforme ou immobile, la somme des forces s’exerçant sur le ballon de baudruche est nulle.
2.4.2. Montrer que la valeur de la norme f de la force de frottements exercée par l’air sur le ballon de baudruche entre les positions n°6 et n°9 est égale à 4,7×10-2 N.
Entre les points 6 et 9 : le mouvement est rectiligne uniforme. D’après la première loi de Newton :
\[ \mathrm{ \sum \overrightarrow{F_{\text{ext}}} = 0 }\]
\[ \mathrm{ \overrightarrow{P} + \overrightarrow{F_A} + \overrightarrow{f} = 0 }\]
Projetons sur l’axe \(z\) :
\[ \mathrm{ P – F_A – f = 0 }\]
\[ \mathrm{ -f = -P + F_A }\]
\[ \mathrm{ f = P – F_A }\]
\[ \mathrm{ f = 5{,}94 \times 10^{-2} – 1{,}2 \times 10^{-2} }\]
\[ \mathrm{ f = 4{,}7 \times 10^{-2} \, \text{N} }\]
Ainsi, la valeur de la norme \(f\) de la force de frottement exercée par l’air sur le ballon de baudruche entre les positions n°6 et n°9 est égale à \(4{,}7 \times 10^{-2} \, \text{N}\).
