Le mythique waterslide revient le 21 avril à la Clusaz !

ÉVALUATION – 10 points – Durée 1h – calculatrice autorisée

Sujet 2024 n°SPEPHCH103 et n°SPEPHCH109

Document 1 : Le défi Foly

« Le Défi Foly c’est simple : il suffit de parcourir à skis, monoski, snowboard ou tout engin glissant similaire, la plus grande distance sur le LAC DES CONFINS.

Après une prise d’élan sur une pente raide et enneigée, tentez de battre le record de 155 m ».

Source https://canarddulac.fr/

Document 2 : La piste du défi et les hypothèses de l’étude

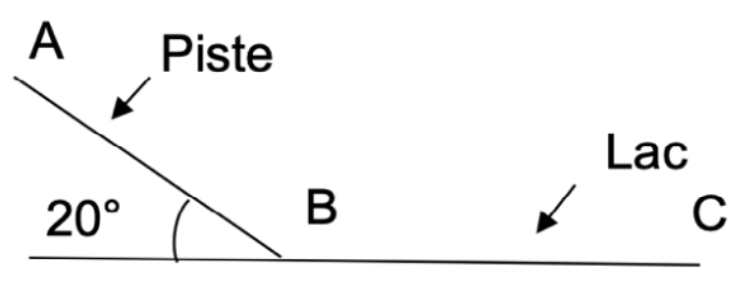
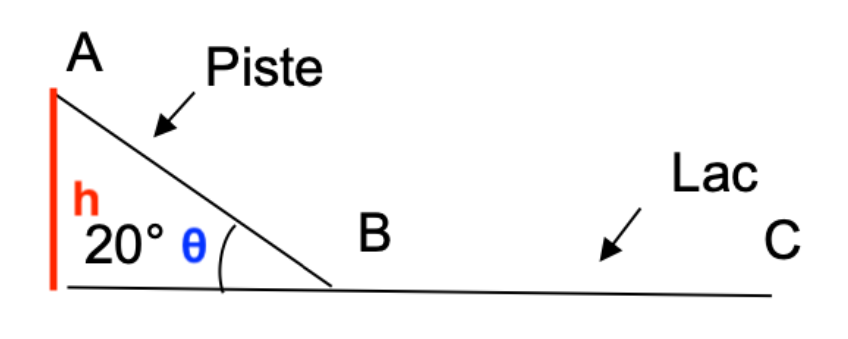
La pente enneigée sur laquelle se situe la piste d’élan est inclinée d’un angle θ = 20,0° par rapport à la surface du lac.

Un skieur part sans vitesse initiale du point A situé sur la piste d’élan, arrive sur l’eau au point B puis glisse sur l’eau jusqu’au point C où il s’arrête, on note AB = d = 60,0 m et BC = D.

Le système {skieur et son équipement} est modélisé par un point matériel et son mouvement est étudié dans le référentiel terrestre supposé galiléen. La masse de ce système est m = 110 kg. On néglige toutes les forces de frottement qui s’exercent sur le système entre A et B et on suppose qu’une force de frottement constante de norme 𝑓 = 200 N s’exerce sur le système entre B et C.

La surface du lac constitue par ailleurs le niveau de référence pour l’énergie potentielle de pesanteur du skieur.

Document 3 : Disposition des spectateurs et du commentateur de la compétition

Les spectateurs et photographes sont placés de part et d’autre de la piste d’élan mais également sur la rive opposée du lac à une distance L = 300 m du point A. Au niveau du départ de la piste d’élan, au point A, se trouve le commentateur de l’épreuve et son dispositif de sonorisation qui permet à tous les spectateurs de suivre la compétition et en particulier d’entendre le top départ.

Document 4 : Caractéristiques de l’appareil photo d’un spectateur

Distance focale de l’objectif : f’ = 100 mm
Capteur “Full Frame” : l’image sur le capteur a pour dimensions 24 mm x 36 mm
Taille de l’écran de visualisation externe : 4,8 cm x 7,2 cm
Une image de hauteur h sur le capteur “Full Frame” sera vue sur l’écran de visualisation avec une hauteur h’ = 20 x h

Source: https://fr.wikipedia.org/wiki/Appareil_photographique_reflex_num%C3%A9rique

Document 5 : Schématisation, relations de conjugaison et de grandissement pour une lentille mince convergente

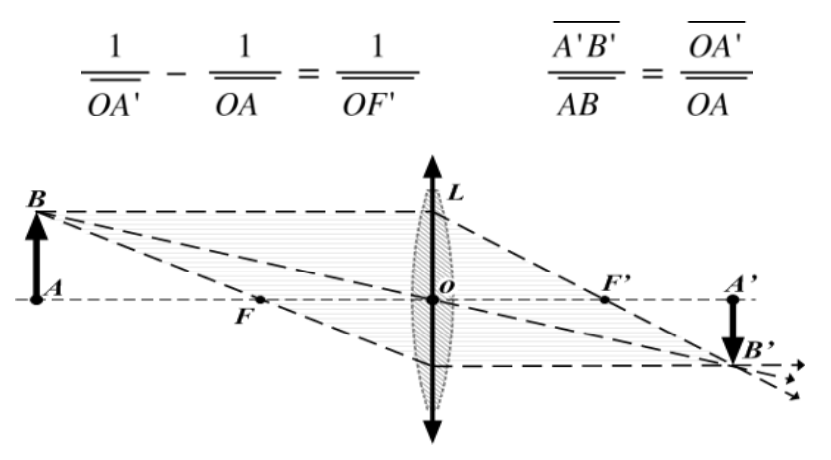
Source : https://fr.wikipedia.org/wiki/Fichier:ThinLens.png

1. Mouvement d’un skieur relevant le défi Foly

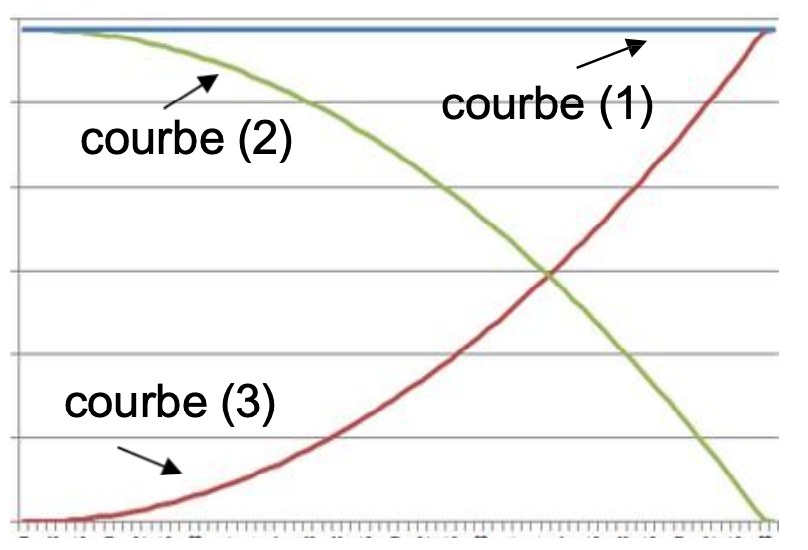
1.a. Le graphique suivant représente une simulation de l’allure des variations des énergies du système (en ordonnée) en fonction du temps (en abscisse) lors de la descente de la piste d’élan.

Identifier en justifiant votre choix :

la courbe représentant l’évolution de l’énergie mécanique.
la courbe représentant l’évolution de l’énergie cinétique ;
la courbe représentant l’évolution de l’énergie potentielle de pesanteur ;

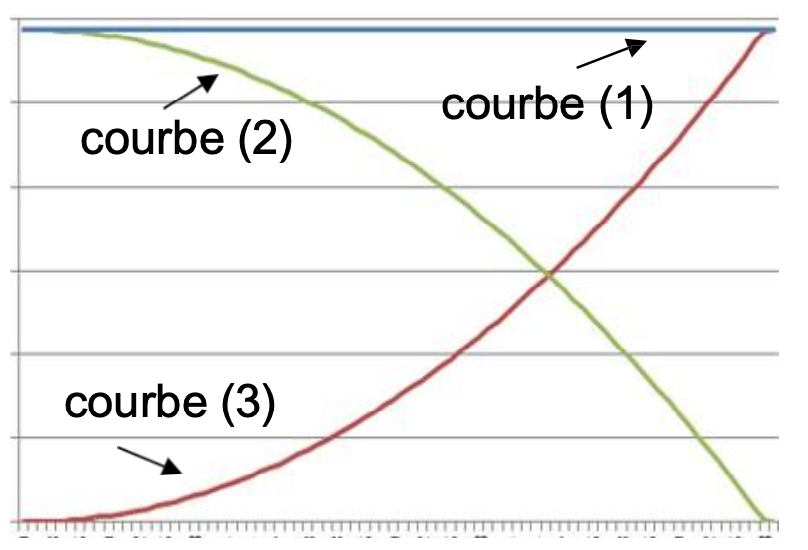
Epp = m × g × z : l’énergie potentielle de pesanteur est proportionnelle à l’altitude. Entre les points A et B, l’altitude z diminue donc Epp diminue : Courbe (2)

Ec =1/2×m×v² : Le skieur part sans vitesse initiale. Ainsi, à l’instant initiale, la vitesse étant nulle, l’énergie cinétique est nulle. Lors de la décente, la vitesse augmente donc l’énergie cinétique augmente : courbe (3)

Em =Ec +Epp : l’énergie mécanique est la somme de l’énergie cinétique et l’énergie potentielle de pesanteur. La courbe la représentant est la somme des deux autres : courbe (1)

Autre justification possible pour l’énergie mécanique : l’énoncé nous indique qu’on néglige toutes les forces de frottement qui s’exercent sur le système entre A et B. L’énergie mécanique se conserve, la courbe la représentant est constante : courbe (1)

1.b. En utilisant le document 2, calculer la valeur de la hauteur du point A par rapport au lac.

$\mathrm{ \sin(\theta) = \frac{\text{Opposé}}{\text{Hypoténuse}} }$

$\mathrm{ \sin(\theta) = \frac{h}{AB} }$

$\mathrm{ \frac{h}{AB} = \sin(\theta) }$

$\mathrm{ h = \sin(\theta) \times AB }$

$\mathrm{ h = \sin(20{,}0^\circ) \times 60{,}0 }$

$\mathrm{ h = 20{,}5 \, \text{m} }$

La hauteur du point A par rapport au lac est de 20,5 m.

1.c. Déterminer au point A les valeurs de :

l’énergie cinétique ;
l’énergie potentielle de pesanteur ;
l’énergie mécanique.

Donnée : intensité de la pesanteur g = 9,80 m.s^-2

$\mathrm{ E_c(A) = \frac{1}{2} \times m \times v_A^2}$

$\mathrm{ E_c(A) = \frac{1}{2} \times 110 \times 0^2 }$

$\mathrm{ E_c(A) = 0 \, \text{J}}$

$\mathrm{ E_{pp}(A) = m \times g \times z_A}$

$\mathrm{ E_{pp}(A) = m \times g \times h }$

$\mathrm{ E_{pp}(A) = 110 \times 9{,}80 \times 20{,}5 }$

$\mathrm{ E_{pp}(A) = 2{,}21 \times 10^4 \, \text{J}}$

$\mathrm{ E_m(A) = E_c(A) + E_{pp}(A) }$

$\mathrm{ E_m(A) = 0 + 2{,}21 \times 10^4 }$

$\mathrm{ E_m(A) = 2{,}21 \times 10^4 \, \text{J} }$

1.d. On suppose pour la suite que l’énergie mécanique du système au point A vaut E_mA = 22,1 kJ. En considérant qu’il y a conservation de l’énergie mécanique, vérifier que la vitesse atteinte par le skieur en bas de la pente enneigée, c’est-à-dire au point B, est égale à 20,0 m.s^-1.

En considérant qu’il y a conservation de l’énergie mécanique :

$\mathrm{ E_m(B) = E_m(A) }$

$\mathrm{ E_c(B) + E_{pp}(B) = E_m(A)}$

$\mathrm{ \frac{1}{2} \times m \times v_B^2 + m \times g \times z_B = E_m(A) }$

$\mathrm{ \frac{1}{2} \times m \times v_B^2 + m \times g \times 0 = E_m(A) }$

$\mathrm{ \frac{1}{2} \times m \times v_B^2 = E_m(A) }$

$\mathrm{ v_B^2 = \frac{2 \times E_m(A)}{m} }$

$\mathrm{ v_B = \sqrt{\frac{2 \times E_m(A)}{m}} }$

$\mathrm{ v_B = \sqrt{\frac{2 \times 2{,}21 \times 10^4}{110}} }$

$\mathrm{ v_B = 20{,}0 \, \text{m} \cdot \text{s}^{-1} }$

En considérant qu’il y a conservation de l’énergie mécanique, la vitesse atteinte par le skieur en bas de la pente enneigée, c’est-à-dire au point B, est égale à 20,0 m.s^-1.

1.e. En appliquant au système le théorème de l’énergie cinétique entre B et C, montrer que l’on obtient l’équation suivante : $\frac{1}{2} m V_C^2 - \frac{1}{2} m V_B^2 = -f \times D$ où 𝑉_Cet V_B désignent respectivement la norme des vitesses en C et B.

Les forces s’exerçant entre B et C sont :

– Le poids $\overrightarrow{P}$

– La réaction normale $\overrightarrow{R_N}$

– Les forces de frottement $\overrightarrow{f}$

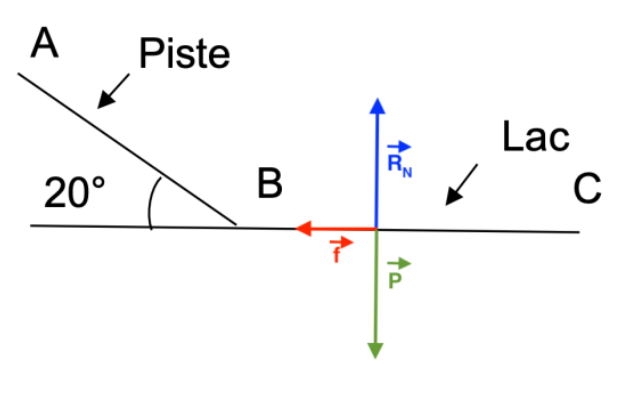
Théorème de l’énergie cinétique entre B et C :

$\mathrm{\Delta E_c = \sum \limits_{\text{forces}} W_{BC}(\overrightarrow{F})}$

$\mathrm{E_c(C) - E_c(B) = W_{BC}(\overrightarrow{P}) + W_{BC}(\overrightarrow{R_N}) + W_{BC}(\overrightarrow{f})}$

$\mathrm{\frac{1}{2} \times m \times V_C^2 - \frac{1}{2} \times m \times V_B^2 = \overrightarrow{P} \cdot \overrightarrow{BC} + \overrightarrow{R_N} \cdot \overrightarrow{BC} + \overrightarrow{f} \cdot \overrightarrow{BC}}$

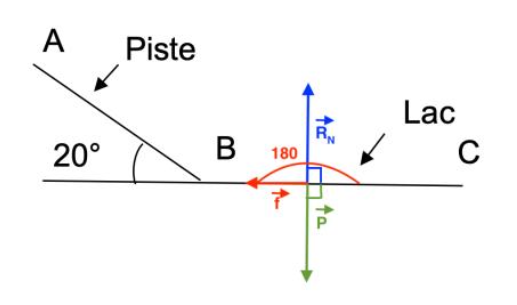
$\mathrm{\frac{1}{2} \times m \times V_C^2 - \frac{1}{2} \times m \times V_B^2 = P \times BC \times 0 + R_N \times BC \times 0 + f \times BC \times (-1)}$

$\mathrm{\frac{1}{2} \times m \times V_C^2 - \frac{1}{2} \times m \times V_B^2 = -f \times BC}$

$\mathrm{\frac{1}{2} \times m \times V_C^2 - \frac{1}{2} \times m \times V_B^2 = -f \times D}$

1.f. En déduire que la distance D parcourue par ce skieur sur le lac est égale à 110 m.

$\mathrm{\frac{1}{2} \times m \times V_C^2 - \frac{1}{2} \times m \times V_B^2 = -f \times D}$

$\mathrm{-f \times D = \frac{1}{2} \times m \times V_C^2 - \frac{1}{2} \times m \times V_B^2}$

$\mathrm{D = \frac{\frac{1}{2} \times m \times V_C^2 - \frac{1}{2} \times m \times V_B^2}{-f}}$

$\mathrm{D = \frac{\frac{1}{2} \times 110 \times 0^2 - \frac{1}{2} \times 110 \times 20{,}0^2}{-200}}$

$\mathrm{D = 110 \, \text{m}}$

Ainsi, la distance D parcourue par ce skieur sur le lac est égale à 110 m.

1.g. Le résultat vous semble-t-il en cohérence avec les informations données dans le document 1 ?

Le document 1 indique que le record est de 155 m.

La distance parcourue par notre skieur est éloignée du record. Cependant, cette distante est du même ordre de grandeur que le record.

Le document 1 ajoute : Le Défi Foly c’est simple : il suffit de parcourir à skis, monoski, snowboard ou tout engin glissant similaire, la plus grande distance sur le LAC DES CONFINS.

Pour augmenter cette distance il doit choisir un autre engin qui diminuera la force de frottement.

2. Photo du départ ratée ou réussie ?

2.a. Un spectateur est situé sur la rive opposée du lac à une distance L = 300 m du point A. Il souhaite prendre une photo avec un cadrage en gros plan d’un participant à l’instant où il s’élance du point A. Il appuie donc sur le déclencheur de son appareil photo au moment où il entend le top départ donné par le commentateur situé près de la ligne de départ au point A.

Après visionnage de la photo sur son écran, il s’exclame : « J’ai raté le départ ! ».

Calculer les durées nécessaires au son et à la lumière pour parcourir la distance entre le point A et le spectateur. Expliquer la réaction du photographe amateur.

Données : célérité des ondes sonores dans l’air c_son = 341 m.s^-1 ;

célérité des ondes lumineuses dans l’air c_lum = 3,00 x 10⁸ m.s^-1.

2.b. Ce même spectateur est également déçu de sa photo pour une autre raison.

$\mathrm{ c = \frac{d}{\Delta t}}$

$\mathrm{ c = \frac{L}{\Delta t}}$

$\mathrm{ c \times \Delta t = L}$

$\mathrm{ \Delta t = \frac{L}{c}}$

Pour le son :

$\mathrm{ \Delta t_{\text{son}} = \frac{L}{c_{\text{son}}}}$

$\mathrm{ \Delta t_{\text{son}} = \frac{300}{341}}$

$\mathrm{ \Delta t_{\text{son}} = 8{,}80 \times 10^{-1} \, \text{s}}$

Pour la lumière :

$\mathrm{ \Delta t_{\text{lum}} = \frac{L}{c_{\text{lum}}}}$

$\mathrm{ \Delta t_{\text{lum}} = \frac{300}{3{,}00 \times 10^8}}$

$\mathrm{ \Delta t_{\text{lum}} = 1{,}00 \times 10^{-6} \, \text{s}}$

$\mathrm{ \Delta t_{\text{lum}} \ll \Delta t_{\text{son}} :}}$

la lumière est beaucoup plus rapide que le son. Ainsi, en se basant sur le son, le photographe amateur a déclenché sa photo 0,88 s plus tard. Il a donc raté le départ.

2.b.1 Déterminer la taille h₁ de l’image du skieur qui se forme sur le capteur “Full Frame” de l’appareil photo sachant que le skieur mesure h = 1,80 m.

La taille h₁ de l’image du skieur qui se forme sur le capteur “Full Frame” est la taille de l’image $\overline{A'B'}$

$\mathrm{\frac{\overline{A'B'}}{\overline{AB}} = \frac{\overline{OA'}}{\overline{OA}}}$

$\mathrm{\overline{A'B'} = \frac{\overline{OA'}}{\overline{OA}} \times \overline{AB}}$

Utilisons la relation de conjugaison pour isoler $\overline{OA'}$ :

$\mathrm{\frac{1}{\overline{OA'}} - \frac{1}{\overline{OA}} = \frac{1}{f'}}$

$\mathrm{\frac{1}{\overline{OA'}} = \frac{1}{f'} + \frac{1}{\overline{OA}}}$

$\mathrm{\frac{1}{\overline{OA'}} = \frac{1 \times \overline{OA}}{f' \times \overline{OA}} + \frac{1 \times f'}{\overline{OA} \times f'}}$

$\mathrm{\frac{1}{\overline{OA'}} = \frac{\overline{OA} + f'}{f' \times \overline{OA}}}$

$\mathrm{\overline{OA'} = \frac{f' \times \overline{OA}}{\overline{OA} + f'}}$

Ainsi,

$\mathrm{\overline{A'B'} = \frac{\overline{OA'}}{\overline{OA}} \times \overline{AB}}$

$\mathrm{\overline{A'B'} = \frac{f' \times \overline{OA}}{(\overline{OA} + f') \times \overline{OA}} \times \overline{AB}}$

$\mathrm{\overline{A'B'} = \frac{f'}{\overline{OA} + f'} \times \overline{AB}}$

$\mathrm{\overline{A'B'} = \frac{100 \times 10^{-3}}{-300 + 100 \times 10^{-3}} \times 1{,}8}$

$\mathrm{\overline{A'B'} = -6{,}0 \times 10^{-4} \, \text{m}}$

$\mathrm{\overline{A'B'} = -0{,}6 \, \text{mm}}$

h₁ =-0,6 mm

La taille h₁ de l’image du skieur qui se forme sur le capteur “Full Frame” à pour valeur 0,6 mm.

2.b.2 À l’aide du document 4, en déduire la taille h₁’ de l’image du skieur sur l’écran de visualisation de l’appareil photo et expliquer la déception du spectateur à la vue de la photo qu’il a prise.

D’après le document 4 : « Une image de hauteur h sur le capteur “Full Frame” sera vue sur l’écran de visualisation avec une hauteur h’ = 20 x h »

$\mathrm{h_1' = 20 \times h_1}$

$\mathrm{h_1' = 20 \times 6{,}0 \times 10^{-4} \, \text{m}}$

$\mathrm{h_1' = 1{,}2 \times 10^{-2} \, \text{m}}$

$\mathrm{h_1' = 1{,}2 \, \text{cm}}$

Sur l’écran de visualisation de l’appareil photo, le skieur mesure 1,2 cm.

La taille de l’écran de visualisation externe : 4,8 cm x 7,2 cm.

L’image du skieur occupe une petite partie de l’écran. C’est ce qui peut expliquer la déception du spectateur à la vue de la photo qu’il a prise.