Mouvement d’une balançoire bouée

ÉVALUATION – 10 points – Durée 1h – calculatrice autorisée

Sujet 2024 n°SPEPHCH104 et n°SPEPHCH111

Document 1 : Balançoire bouée vendue dans le commerce

Image : https://www.manomano.fr/p/balancoire- bouee-pour-enfant-591754

Document 2

Les concepteurs de cette balançoire « bouée » destinée aux enfants ont besoin de tester la résistance du jeu et d’étudier le risque de rupture de la corde avant la mise sur le marché du produit.

Ils souhaitent vérifier à quel moment la corde a le plus de risque de se rompre.

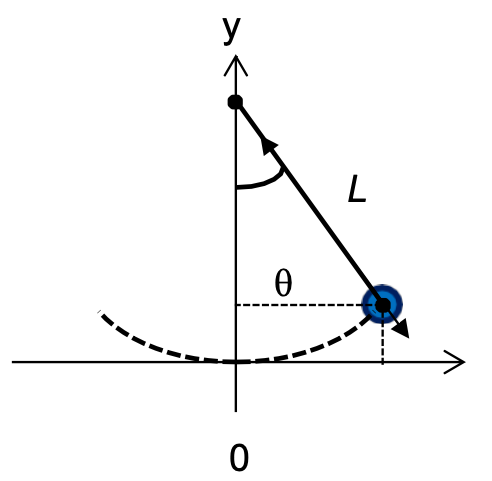
Pour simuler le mouvement de l’enfant sur la balançoire bouée, l’enregistrement vidéo des positions successives d’une bille suspendue à un fil est réalisé. La bille est lâchée depuis sa position la plus haute sans vitesse initiale, à t = 0 s.

L’origine du repère correspond à la position verticale du fil, comme indiqué sur le schéma ci-dessus.

La balançoire bouée est modélisée par une bille suspendue à un fil inextensible de masse

m = 25 g et de longueur L = 40 cm. Le système est soumis à son poids $\overrightarrow{P}$ ainsi qu’à la force $\overrightarrow{T}$ exercée par le fil.

Les frottements de l’air sont négligés.

Données : intensité de la pesanteur : g = 9,81 m.s^-2

Document 3

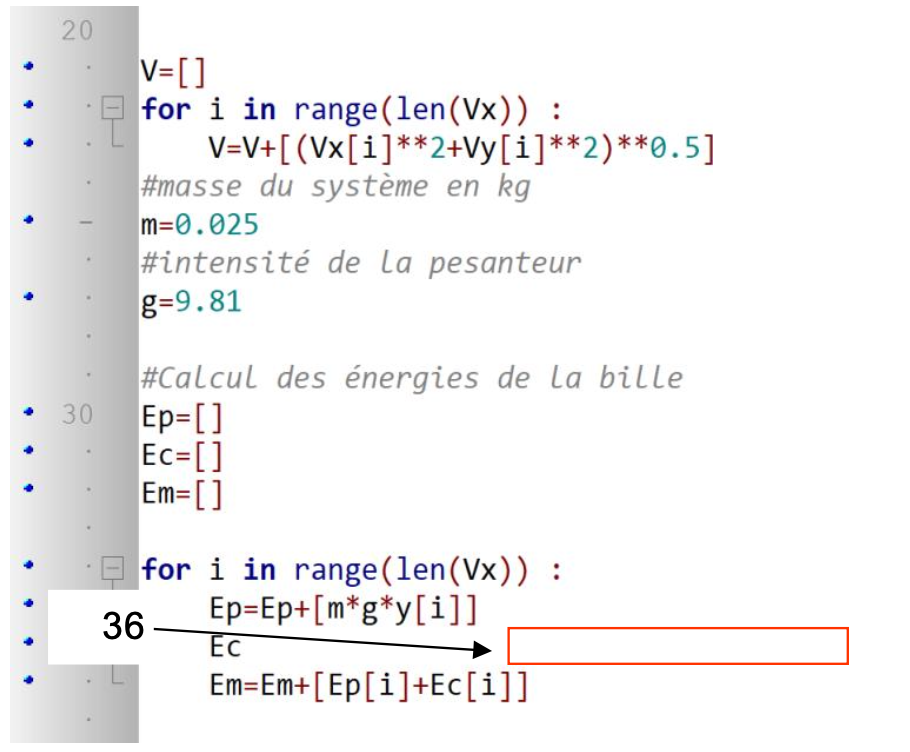
Document 4 : Programme informatique en langage Python

Vx et Vy représentent les composantes du vecteur vitesse de la bille suivant x et y.

Document 5

L’utilisation des lois de la mécanique permet d’établir l’expression de la norme de la force T exercée par le fil :

$\mathrm{ T = m \cdot g \cdot \cos \theta + \frac{m \cdot v^2}{L}}$

avec

m masse de la bille exprimée en kilogramme ;
g intensité de la pesanteur exprimée en m.s^-2 ;
θ angle entre le fil et la verticale ;
v la vitesse de la bille en un point de sa trajectoire exprimée en m.s-1 ;
L la longueur du fil exprimée en mètre.

Document 6 : Représentation graphique de l’évolution des énergies de la bille

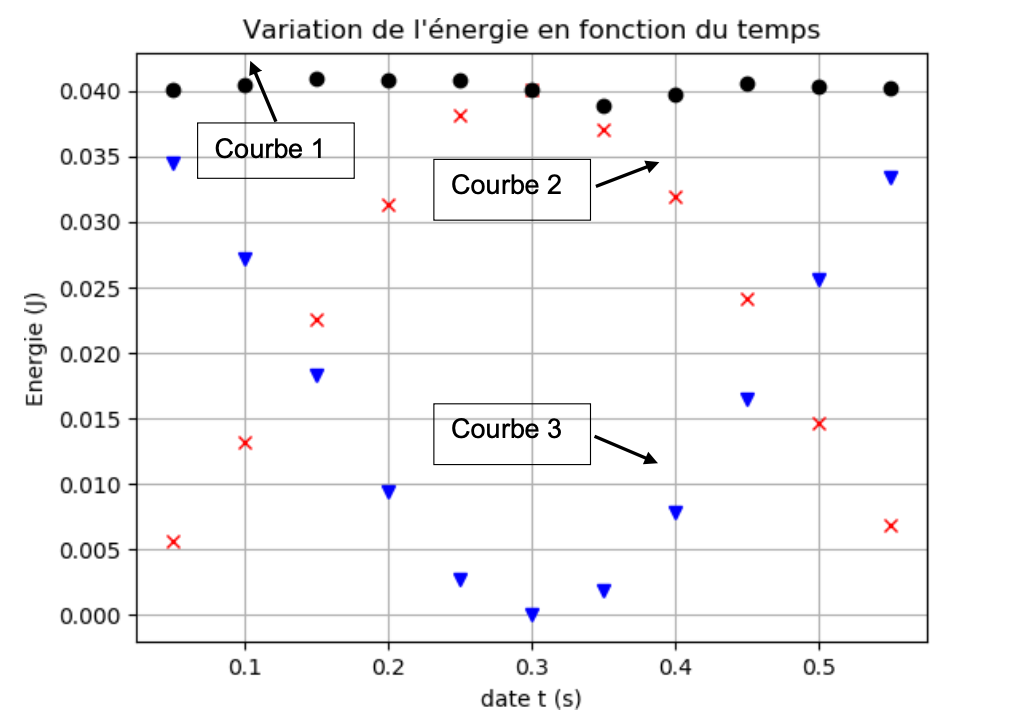
1. Les concepteurs de la balançoire « bouée » veulent identifier la zone où la vitesse atteinte sera maximale. Ils réalisent une étude énergétique du mouvement de la bille suspendue à un fil.

Un programme informatique (document 4) écrit en langage Python permet de tracer les courbes représentant l’évolution des énergies cinétique, potentielle de pesanteur et mécanique du système au cours du temps.

1.1. Écrire la ligne de code n°36 permettant de calculer l’énergie cinétique du système. Les courbes obtenues avec le programme figurent sur le document 6.

L’énergie cinétique est définie par : Ec =1/2×m×v²
En langage Python, la ligne de code n°36 s’écrit : Ec=0.5*m*V[i]**2

1.2. Attribuer à chaque courbe l’énergie qui lui correspond en justifiant la réponse.

La bille est lâchée depuis sa position la plus haute sans vitesse initiale, à t = 0 s.

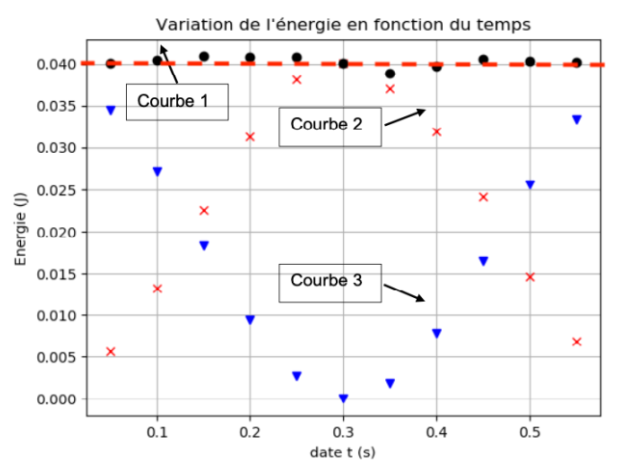
Epp = m × g × y : l’énergie potentielle de pesanteur est proportionnelle à l’altitude. Initialement l’altitude est grande (position la plus haute) et après le lâché, l’altitude y diminue donc Epp diminue : Courbe 3

Ec =1/2×m×v² : La bille est lâchée sans vitesse initiale la vitesse initiale. Ainsi, à l’instant initiale, la vitesse étant nulle, l’énergie cinétique est nulle. Lors de la décente, la vitesse augmente donc l’énergie cinétique augmente : Courbe 2

Em =Ec +Epp : l’énergie mécanique est la somme de l’énergie cinétique et l’énergie potentielle de pesanteur. La courbe la représentant est la somme des deux autres : Courbe 1

1.3. Déterminer la valeur de la hauteur initiale de la bille.

L’énergie potentielle initiale est donnée par :

$\mathrm{ E_{\text{pp}_0} = m \times g \times y_0}$

$\mathrm{ m \times g \times y_0 = E_{\text{pp}_0}}$

$\mathrm{ y_0 = \frac{E_{\text{pp}_0}}{m \times g}}$

Graphiquement, $E_{\text{pp}_0} = E_{m_0} = 0{,}040 \text{ J}$ car au début il n’y a pas de vitesse et donc pas d’énergie cinétique. Ainsi,

$\mathrm{ y_0 = \frac{0{,}040}{25 \times 10^{-3} \times 9{,}81}}$

$\mathrm{ y_0 = 0{,}16 \text{ m}}$

$\mathrm{ y_0 = 16 \text{ cm}}$

1.4. Déterminer la valeur de la vitesse maximale acquise. À quelle position de la bille cela correspond-il ?

La valeur de la vitesse maximale est acquise pour Ec_max=Em=0,040 J. L’énergie potentielle de pesanteur est nulle.

$\mathrm{ E_{\text{c}_\text{max}} = E_m = 0{,}040 \text{ J}}$

$\mathrm{ \frac{1}{2} \times m \times v_{\text{max}}^2 = E_{\text{c}_\text{max}}}$

$\mathrm{ v_{\text{max}}^2 = \frac{2 \times E_{\text{c}_\text{max}}}{m}}$

$\mathrm{ v_{\text{max}} = \sqrt{\frac{2 \times E_{\text{c}_\text{max}}}{m}}}$

$\mathrm{ v_{\text{max}} = \sqrt{\frac{2 \times 0{,}040}{25 \times 10^{-3}}}}$

$\mathrm{ v_{\text{max}} = 1{,}8 \text{ m/s}}$

La vitesse maximale est acquise a pour valeur v_max=1,8 m.s^-1.

La valeur de la vitesse maximale est acquise lorsque l’altitude est minimale au point (0,0).

1.5. L’hypothèse de négliger les frottements est-elle valide ? Justifier la réponse.

L’énergie mécanique (Courbe 1) est constante au cours du temps. Les forces de frottements sont donc négligeables. L’hypothèse de négliger les frottements est donc valide.

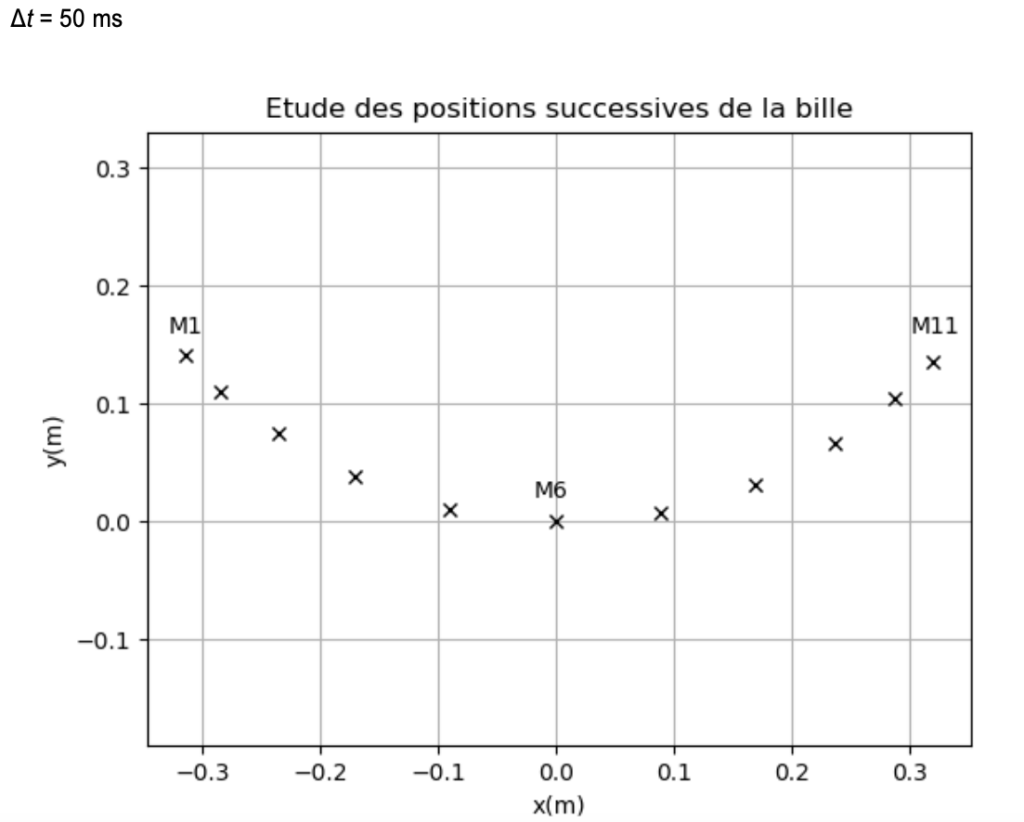
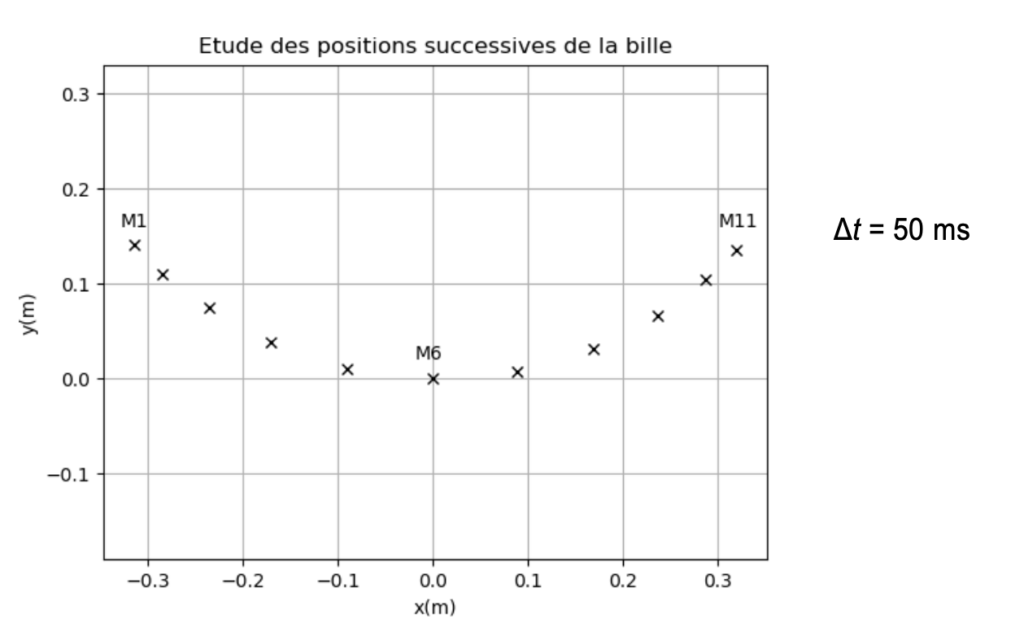
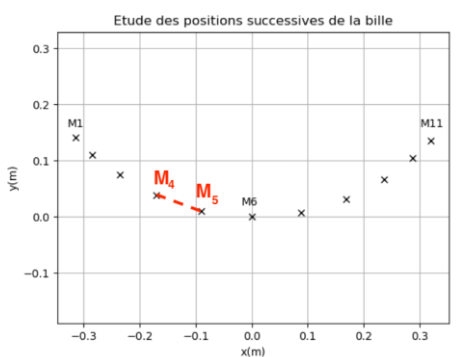
2. Pour simuler le mouvement de l’enfant sur la balançoire bouée, les positions successives de la bille sont enregistrées (document 3).

2.1. Décrire le mouvement de la bille entre les points M₁ et M₆.

Entre les points M₁ et M₆ :

La trajectoire est un arc de cercle
La distance entre les points augmente

Ainsi, entre les points M₁ et M₆ le mouvement est circulaire accéléré.

2.2. Que peut-on en déduire, sur ce parcours, des forces exercées sur la bille ? Justifier la réponse.

Le mouvement n’est pas rectiligne uniforme, d’après la première loi de Newton : les forces appliquées au système ne s’annulent pas.

2.3. Calculer la norme du vecteur vitesse au point 4, puis construire le vecteur vitesse au point 4 sur l’annexe à rendre avec la copie en utilisant l’échelle : 1 cm ↔ 0,5 m.s^-1.

Schéma	Réel
2,0 cm	0,1 m
1,7 cm	M₄M₅

$\mathrm{ M_{4\,5} = \frac{1{,}7 \times 0{,}1}{2{,}0}}$

$\mathrm{ M_{4\,5} = 0{,}085 \text{ m}}$

$\mathrm{ v_4 = \frac{M_{4\,5}}{\Delta t}}$

$\mathrm{ v_4 = \frac{0{,}085}{50 \times 10^{-3}}}$

$\mathrm{ v_4 = 1{,}7 \text{ m/s}}$

1 cm	0,5 m.s^-1
d	1,7 m.s^-1

$\mathrm{ d = \frac{1{,}7 \times 1}{0{,}5}}$

$\mathrm{ d = 3{,}4 \text{ cm}}$

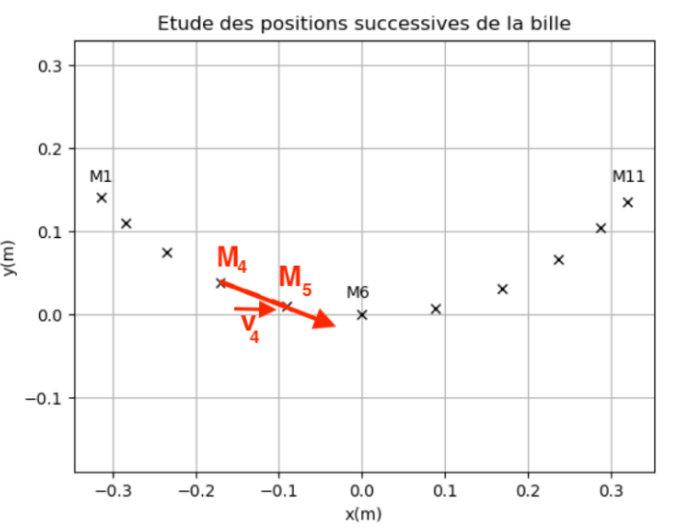
On représente le vecteur vitesse au point 4 par une flèche :

D’une longueur 3,4 cm (norme)
Dont l’origine est au point 4 (point d’origine)
Tangente à la trajectoire (direction)
Dans le sens du mouvement (sens)

On traite numériquement les positions de la bille leur permettant d’obtenir sa vitesse entre les positions 1 et 11.

Les résultats sont notés dans le tableau suivant :

Position de la bille	M1	M2	M3	M4	M5	M6	M7	M8	M9	M10	M11
Vitesse (en m.s^-1)	0,86	1,20	1,49		1,82	1,79	1,68	1,53	1,26	0,92	0,56

2.4. À l’aide du document 5, calculer la valeur de la norme de la force T₅ exercée par le fil au point 5 sachant que l’angle 𝜃 est égal à 13°.

Le document 5 nous donne :

$\mathrm{ T = m \cdot g \cdot \cos \theta + \frac{m \cdot v^2}{L} }$

$\mathrm{ T_5 = m \cdot g \cdot \cos \theta + \frac{m \cdot v_5 ^2}{L} }$

$\mathrm{ T_5 = 25 \times 10^{-3} \cdot 9{,}81 \cdot \cos 13^\circ + \frac{25 \times 10^{-3} \cdot 3{,}3124}{40 \times 10^{-2}} }$

$\mathrm{ T_5 = 0{,}45 \text{ N} }$

2.5. La tension T₁₁du fil au point 11 est égale à 0,18 N. Comparer T₅ et T₁₁.

$\mathrm{ T_5 = 0{,}45 \text{ N} }$

$\mathrm{ T_{11} = 0{,}18 \text{ N} }$

Ainsi $T_5 > T_{11}$ .

2.6. En déduire qualitativement pour quelles positions de la balançoire bouée le risque de rupture du fil est le plus fort.

$\mathrm{ T = m \cdot g \cdot \cos \theta + \frac{m \cdot v^2}{L}}$

T augmente quand le cos θ augmente. cos θ est maximal quand θ=0° : position M₆.

T augmente quand la vitesse augmente. La vitesse est maximale quand l’altitude est nulle : position M₆.

Ainsi, la position de la balançoire bouée pour laquelle le risque de rupture du fil est le plus fort est la position M₆.

Annexe à rendre avec la copie

Question 2.3