ÉVALUATION – 10 points – Durée 1h – calculatrice autorisée
Sujet 2024 n°SPEPHCH120 et n°SPEPHCH122
Télécharger l’exercice en PDF :
Les smartphones disposent de capteurs performants qui permettent d’accéder à des grandeurs physiques par des mesures directes ou indirectes. Dans ce sujet, on utilise un smartphone pour déterminer l’altitude d’une salle d’un lycée et la vitesse de l’ascenseur pour y accéder.
1. Altitude d’une salle de lycée
On pose un smartphone au sol du rez-de- chaussée d’un lycée et on active le capteur de pression. On observe que la valeur affichée fluctue. On décide de relever la valeur de la pression, notée PRDC, toutes les cinq secondes, à huit reprises. On monte ensuite au 4ème étage du lycée et, de la même manière, on relève la valeur de la pression, notée P4ème, au sol du 4ème étage. Les valeurs de pressions mesurées sont indiquées dans le tableau ci-contre.
| Mesure n° | PRDC (hPa) | Mesure n° | P4ème (hPa) |
| 1 | 1016,679 | 1 | 1014,489 |
| 2 | 1016,680 | 2 | 1014,493 |
| 3 | 1016,678 | 3 | 1014,497 |
| 4 | 1016,674 | 4 | 1014,502 |
| 5 | 1016,677 | 5 | 1014,520 |
| 6 | 1016,688 | 6 | 1014,489 |
| 7 | 1016,683 | 7 | 1014,523 |
| 8 | 1016,686 | 8 | 1014,520 |
Données :
- Exploitation d’une série de mesures d’une grandeur X :
Pour une série de mesures pour lesquelles on suppose les conditions de répétabilité vérifiées, on admet que :
- la meilleure estimation de la valeur de la grandeur X est égale à la moyenne 𝑥 des N valeurs 𝑥 mesurées ;
- l’incertitude-type sur une série de mesure de la grandeur X vaut :
\[ \mathrm{ u_x = \frac{s_{n-1}}{\sqrt{N}}}\]
où 𝑁 est le nombre de valeurs 𝑥 mesurées et $s_{n-1}$ l’écart-type expérimental tel que : $ s_{n-1} = \sqrt{\frac{1}{N-1} \times \sum_{i=1}^{N} \left(x_i – \bar{x} \right)^2}$
- 1 hPa = 102 Pa.
Un traitement statistique des données permet de calculer l’écart-type associé à la série de mesure de 𝑃4è𝑚𝑒. Sa valeur est de : sP = 1,46.10-2 hPa.
1.1. Calculer la valeur moyenne, notée $\overline{P_{4ème } }$ , des huit mesures de la pression au sol du 4ème.
$(\overline{ P_{\text{4ème}}})= \frac{1014{,}489 + 1014{,}493 + 1014{,}497 + 1014{,}502 + 1014{,}520 + 1014{,}489 + 1014{,}523 + 1014{,}520}{8}$
\[ \mathrm{ (\overline{ P_{\text{4ème}}})= 1014{,}504 \text{ hPa}}\]
1.2. Calculer la valeur de l’incertitude-type 𝑢𝑃 associée à la série de mesures de la pression au 4ème étage.
\[ \mathrm{ u_x = \frac{s_{n-1}}{\sqrt{N}}}\]
\[ \mathrm{ u_P = \frac{s_P}{\sqrt{N}}}\]
\[ \mathrm{ u_P = \frac{1{,}46 \times 10^{-2}}{\sqrt{8}}}\]
\[ \mathrm{ u_P = 5 \times 10^{-3} \text{ hPa}}\]
1.3. Écrire le résultat de la mesure sous la forme : $P_{\text{4eme}} = \overline{P_{\text{4eme}}} \pm u_P$
\[ \mathrm{ P_{\text{4ème}} = (\overline{ P_{\text{4ème}}}) \pm u_P}\]
\[ \mathrm{ P_{\text{4ème}} = 1014{,}504 \pm 5 \times 10^{-3}}\]
\[ \mathrm{ P_{\text{4ème}} = 1014{,}504 \pm 0{,}005 \text{ hPa}}\]
Données :
- Loi fondamentale de la statique des fluides
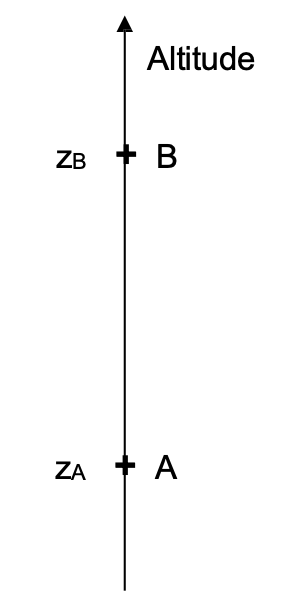
Cette loi relie la différence de pression entre deux points A et B d’un fluide supposé incompressible et leur différence d’altitudes. La loi s’écrit : PA – PB = ρ.g.(zB – zA) avec :
- zA et zB sont les altitudes des points A et B, l’axe des altitudes (Oz) étant orienté suivant la verticale ascendante ;
- ρ est la masse volumique du fluide ;
- g est la valeur de l’intensité de la pesanteur terrestre : g = 9,81 N.kg-1
- on considère que l’air est un fluide incompressible ;
- masse volumique de l’air à 20°C : ρair = 1,204 kg.m-3 ;
- 1 hPa = 102 Pa.
1.4. La valeur moyenne de la pression au rez-de-chaussée obtenue à partir des huit mesures est $\overline{P_{RDC } }= 1016,681 hPa$. Déterminer z4ème, altitude au 4ème étage du lycée l’origine des altitudes étant choisie au rez-de-chaussée.
\[ \mathrm{ P_A – P_B = \rho \cdot g \cdot (Z_B – Z_A)}\]
\[ \mathrm{ \overline{ P_{\text{ RDC }}} – \overline{ P_{\text{4ème}}} = \rho \cdot g \cdot (Z_{\text{4ème}} – Z_{\text{RDC}})}\]
L’origine des altitudes étant choisie au rez-de-chaussée : ZRDC=0 m
\[ \mathrm{ \overline{ P_{\text{ RDC }}} – \overline{ P_{\text{4ème}}} = \rho \cdot g \cdot (Z_{\text{4ème}} – 0)}\]
\[ \mathrm{ \overline{ P_{\text{ RDC }}} – \overline{ P_{\text{4ème}}} = \rho \cdot g \cdot Z_{\text{4ème}}}\]
\[ \mathrm{ \rho \cdot g \cdot Z_{\text{4ème}} =\overline{ P_{\text{ RDC }}} – \overline{ P_{\text{4ème}}} }\]
\[ \mathrm{ Z_{\text{4ème}} = \frac{(1016{,}681 \times 10^2 – 1014{,}504 \times 10^2)}{1{,}204 \times 9{,}81}}\]
\[ \mathrm{ Z_{\text{4ème}} = 18{,}4 \text{ m}}\]
L’altitude au 4ème étage du lycée a pour valeur 18,4 m.
2. Vitesse de déplacement de l’ascenseur
On utilise maintenant le smartphone pour effectuer des mesures de position et de vitesse de l’ascenseur du lycée. On obtient les courbes et le tableau de valeurs suivants :
| Time (s) | Altitude (m) | Time (s) | Altitude (m) |
| 0,32230 | 0 | 31,7772 | 11,6621 |
| 1,33675 | 0,00063 | 33,6554 | 12,7674 |
| 2,35125 | -0,00126 | 35,5337 | 13,8503 |
| 3,36568 | 0 | 37,4121 | 14,9543 |
| 4,38012 | 0 | 39,2900 | 16,0628 |
| 5,48306 | 0,00760 | 41,1678 | 17,1899 |
| 7,36153 | 0,01964 | 43,0457 | 17,9924 |
| 9,24047 | 0,02344 | 44,9235 | 18,4142 |
| 11,1188 | 0,08902 | 46,8012 | 18,5529 |
| 12,9971 | 0,49263 | 48,6793 | 18,5821 |
| 14,8752 | 1,33982 | 50,5573 | 18,5501 |
| 16,7534 | 2,42599 | ||
| 18,6314 | 3,52813 | ||
| 20,5093 | 4,66334 | ||
| 22,3874 | 5,90075 | ||
| 24,2653 | 7,13734 | ||
| 26,1432 | 8,31512 | ||
| 28,0212 | 9,42010 | ||
| 29,8992 | 10,5616 | ||
L’ascenseur de masse m = 550 kg est soumis à deux forces :
- son poids, noté $\overrightarrow{P}$;
- la tension du câble modélisée par une force notée $\overrightarrow{T}$ ,verticale et dirigée vers le haut. La valeur de cette tension varie au cours des différentes phases du mouvement.
Toutes les forces de frottements s’exerçant sur l’ascenseur sont négligées devant les autres forces.
Le mouvement de l’ascenseur est étudié dans le référentiel terrestre supposé galiléen.
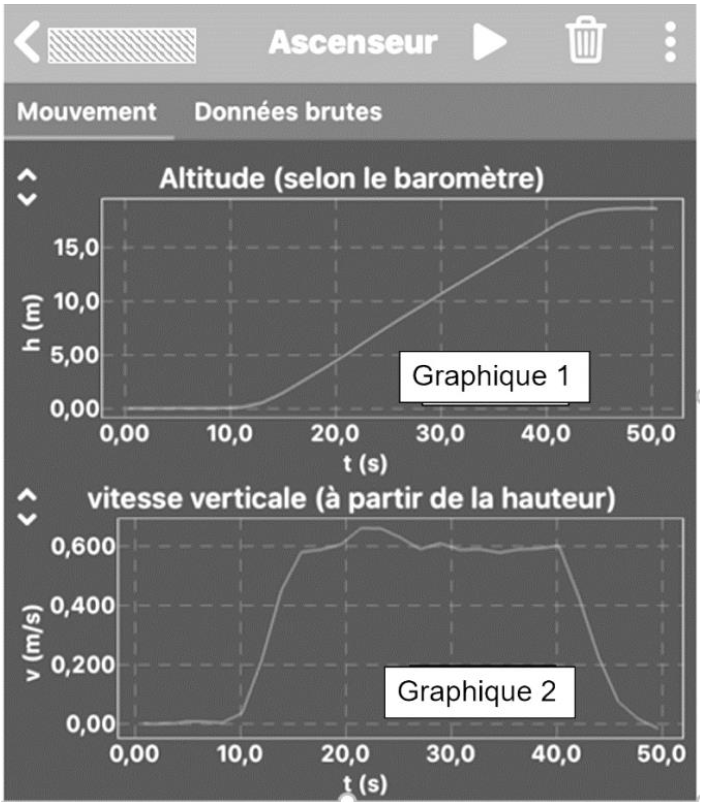
2.1. Décrire le mouvement de l’ascenseur en exploitant les graphes ci-dessus en indiquant les dates de début et de fin de chacune des quatre phases entre 0 s et 50,5 s.
Quatre phases entre 0 s et 50,5 s :
- Entre 0 s et 10 s : l’ascenseur est immobile (vitesse nulle).
- Entre 10 s et 18 s : l’ascenseur monte (l’altitude augmente) et sa vitesse augmente. Le mouvement est rectiligne accéléré.
- Entre 18 s et 40 s : l’ascenseur monte (l’altitude augmente) et sa vitesse est constante. Le mouvement est rectiligne uniforme.
- Entre 40 s et 55 s : l’ascenseur monte (l’altitude augmente) et sa vitesse diminue. Le mouvement est rectiligne décéléré.
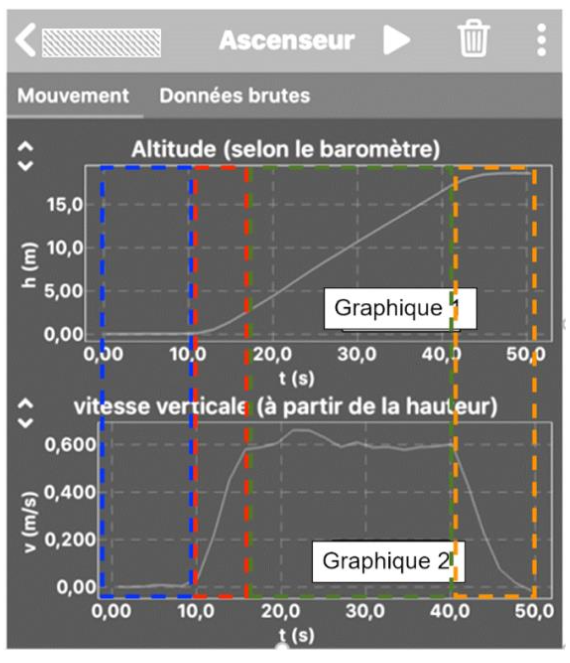
2.2. À partir du graphique 1, déterminer la vitesse de l’ascenseur pendant la phase correspondant au mouvement rectiligne uniforme. Expliquer votre démarche.
Graphiquement, pendant la phase correspondant au mouvement rectiligne uniforme, la vitesse de l’ascenseur a pour valeur 0,600 m/s.
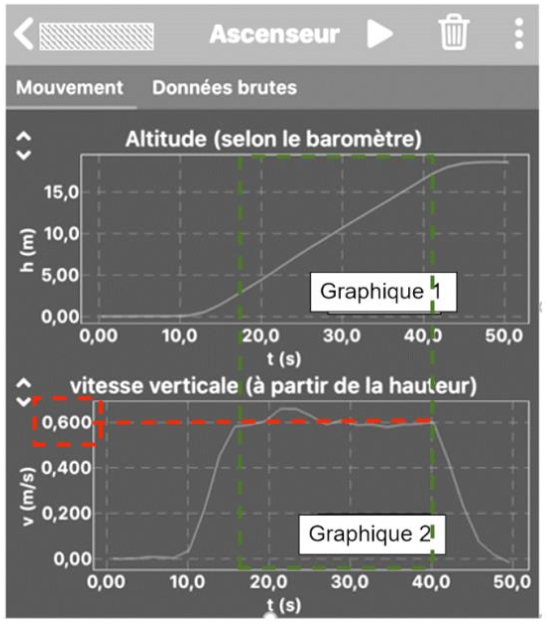
2.3. La notice du constructeur indique une vitesse d’ascension de l’ascenseur de 0,63 m/s. Cette donnée est-elle vérifiée ? Commenter.
La notice du constructeur indique une vitesse d’ascension de l’ascenseur de 0,63 m/s. Or 0,63 m/s ≃ 0,600 m/s.
Ainsi, cette donnée est vérifiée.
2.4. Étude des forces appliquées à l’ascenseur lors de la phase de démarrage.
2.4.1. Calculer la valeur de la norme P du poids du système.
\[ \mathrm{ P = m \times g}\]
\[ \mathrm{ P = 550 \times 9{,}81}\]
\[ \mathrm{ P = 5{,}40 \times 10^3 \text{ N}}\]
2.4.2. En déduire la valeur minimale de la tension pour que l’ascenseur monte.
Le poids est dirigé vers le bas, la tension du câble est dirigée vers le haut. Pour que l’ascenseur monte, il faut que la valeur de la tension soit plus grande que la valeur du poids.
Tmin>P
Tmin>5,40×103 N
Ainsi, pour que l’ascenseur monte, la tension minimale à pour valeur 5,40×103 N.
2.4.3. La vitesse au temps t11 = 11,1 s vaut v11 = 0,21 m/s ; elle vaut v13 = 0,45 m/s à t13 = 13,0 s. Calculer la valeur de la variation de vitesse Δv entre les instants t11= 11,1 s et t13 = 13,0 s.
∆v=v13-v11
∆v=0,45-0,21
∆v=0,24 m/s
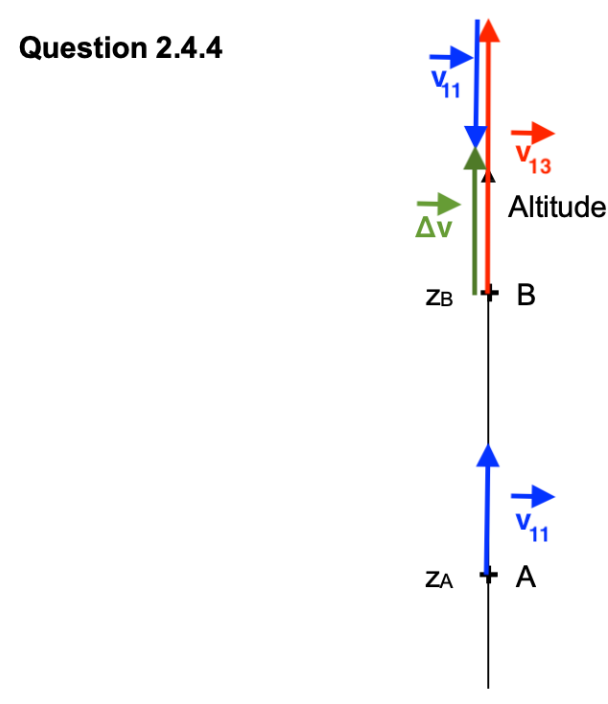
2.4.4. Représenter SUR L’ANNEXE À RENDRE AVEC LA COPIE les 2 vecteurs vitesses $\overrightarrow{v_{11}}$ et $\overrightarrow{v_{13}}$ puis le vecteur variation de vitesse $\overrightarrow{\Delta v}$ entre ces 2 instants à l’échelle 0,10 m.s-1 ↔ 1,0 cm.
| Schéma | Réel |
| 1,0 cm | 0,10 m/s |
| x | 0,45 |
\[ \mathrm{ x = \frac{0{,}45 \times 1{,}0}{0{,}10}}\]
\[ \mathrm{ x = 4{,}5 \text{ cm}}\]
Traçons \( v_{13} \) :
– Point d’application : point B
– Direction : tangent à la trajectoire donc vertical
– Sens : dans le sens du mouvement donc vers le haut
– Valeur : \( v_{13} = 0{,}45 \text{ m/s} \). Représenté par un vecteur de 4,5 cm.
| Schéma | Réel |
| 1,0 cm | 0,10 m/s |
| y | 0,21 |
\[ \mathrm{ y = \frac{0{,}21 \times 1{,}0}{0{,}10}}\]
\[ \mathrm{ y = 2{,}1 \text{ cm}}\]
Traçons \( v_{11} \) :
– Point d’application : point A
– Direction : tangent à la trajectoire donc vertical
– Sens : dans le sens du mouvement donc vers le haut
– Valeur : \( v_{11} = 0{,}21 \text{ m/s} \). Représenté par un vecteur de 2,1 cm.
\[ \mathrm{ (\Delta v) = (v_{13}) – (v_{11})}\]
2.4.5. Montrer que la direction et le sens de ce vecteur variation de vitesse $\overrightarrow{\Delta v}$ entre ces 2 instants sont cohérents avec ceux de la somme des forces appliquées sur le système au démarrage.
D’après la relation approchée de la seconde loi de Newton, \(\sum \overrightarrow{F}\) et \(\overrightarrow{\Delta v}\) ont la même direction et le même sens.
Comparons leurs directions et leurs sens.
– \(\overrightarrow{\Delta v}\) :
– Direction : verticale
– Sens : vers le haut
– \(\sum \overrightarrow{F} = \overrightarrow{P} + \overrightarrow{T}\) :
– Direction : verticale
– Sens : vers le haut
\(\sum \overrightarrow{F}\) et \(\overrightarrow{\Delta v}\) ont la même direction et le même sens.
Ainsi, la direction et le sens du vecteur de variation de vitesse \(\overrightarrow{\Delta v}\) entre ces deux instants sont cohérents avec ceux de la somme des forces appliquées sur le système au démarrage.
ANNEXE À RENDRE AVEC LA COPIE
Question 2.4.4