Températures de surface de la Terre et du Soleil

Sujet avec enseignement de mathématiques spécifique

Enseignement scientifique première

Durée 1h12 – 12 points – Thème « Le Soleil, notre source d’énergie »

Partie 1 – Origine de l’énergie solaire

La Terre reçoit l’essentiel de son énergie du soleil. Cette énergie conditionne sa température de surface.

1 – Préciser le phénomène physique à l’origine de l’énergie dégagée par le soleil.

Une étoile est le siège de fussions nucléaires. Des atomes d’hydrogène fusionnent pour former de l’hélium. Cette réaction s’accompagne d’une grande libération d’énergie notamment sous forme de lumière.

2 – A partir de la relation d’Einstein : E = ∆m × c², calculer la masse solaire transformée chaque seconde en énergie, sachant que l’énergie émise chaque seconde par le soleil a pour valeur 3,9×10²⁶ J.

Donnée : vitesse de la lumière dans le vide c = 3,0×10⁸ m·s^–1

$E = \Delta m \times c^2$

$\Delta m \times c^2 = E$

$\Delta m = \frac{E}{c^2}$

$\text{Remarque : } 1~\text{W} = 1~\text{J.s}^{-1}$

$E = P \times \Delta t$

$\Delta m = \frac{P \times \Delta t}{c^2}$

$\Delta m = \frac{3,9 \times 10^{26} \times 13,0 \times 10^8}{c^2}$

$\Delta m = 4,3 \times 10^9 ~\text{kg.s}^{-1}$

$  La masse solaire transformée chaque seconde en énergie est de 4,3x10<sup>9</sup> Kg.   <strong>Partie 2 - Température de surface du Soleil</strong>   L'étude du spectre du rayonnement émis par le Soleil, que l'on peut modéliser comme un spectre de corps noir, permet de déterminer la température de la surface du Soleil.   À l'aide du document 1 fourni sur la page ci-après, répondre aux questions 3 à 5 :   3 - Déterminer graphiquement les longueurs d'ondes correspondant au maximum d'émission pour les températures de 4000 K, 5000 K et 6000 K. Décrire qualitativement l'évolution de la longueur d'onde au maximum d'émission en fonction de la température du corps.   <div class="wp-block-media-text has-media-on-the-right is-stacked-on-mobile"><div class="wp-block-media-text__content">   <figure class="wp-block-table"><table class="has-vivid-red-color has-text-color has-link-color has-fixed-layout"><tbody><tr><td class="has-text-align-center" data-align="center">Températures (K)</td><td class="has-text-align-center" data-align="center">Longueurs d'ondes correspondant au maximum d'émission (nm)</td></tr><tr><td class="has-text-align-center" data-align="center">4000</td><td class="has-text-align-center" data-align="center">700</td></tr><tr><td class="has-text-align-center" data-align="center">5000</td><td class="has-text-align-center" data-align="center">580</td></tr><tr><td class="has-text-align-center" data-align="center">6000</td><td class="has-text-align-center" data-align="center">480</td></tr></tbody></table></figure> </div><figure class="wp-block-media-text__media"><img src="https://physik.fr/wp-content/uploads/2025/09/Capture-decran-2025-10-12-a-11.35.09.png" alt="" class="wp-image-13094 size-full"/></figure></div>   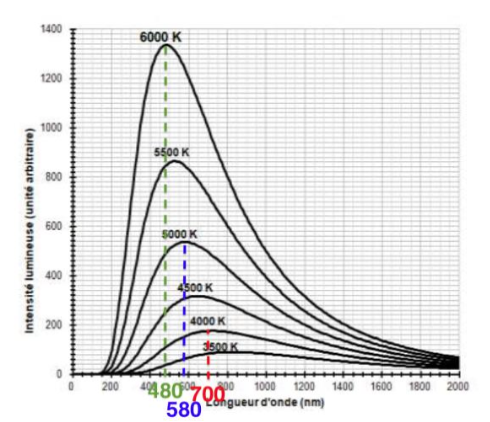Lorsque la température du corps augmente, la longueur d'onde au maximum d'émission diminue.   4 - Justifier à partir de la valeur de la longueur d'onde d'émission maximale du spectre solaire que la température du Soleil est comprise entre 5500 K et 6000 K.   <div class="wp-block-media-text has-media-on-the-right is-stacked-on-mobile"><div class="wp-block-media-text__content"> Pour le Soleil,<strong>λ</strong>max=500 nm. . Cette longueur d'onde au maximum d'émission est comprise entre celle de la courbe pour 5500 K et 6000 K.   Ainsi, la température du Soleil est comprise entre 5500 K et 6000 K. 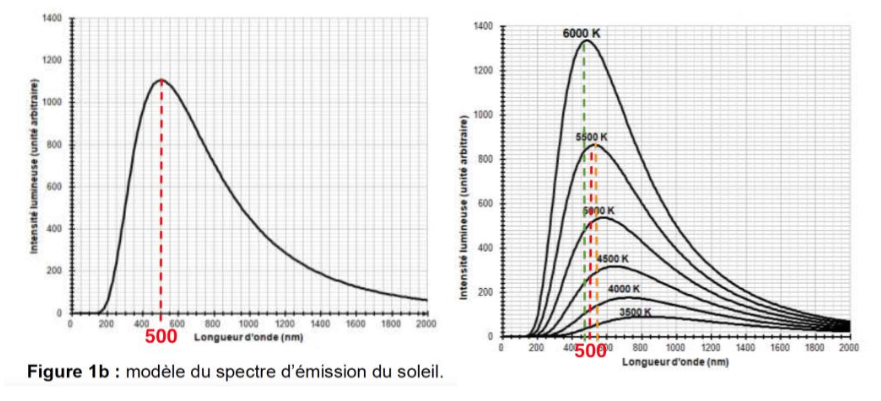</div><figure class="wp-block-media-text__media"><img src="https://physik.fr/wp-content/uploads/2025/09/Capture-decran-2025-10-12-a-11.35.25.png" alt="" class="wp-image-13095 size-full"/></figure></div>   <strong>Document 1 - Spectres d'émission</strong>   <figure class="wp-block-image size-full"><img src="https://physik.fr/wp-content/uploads/2025/09/Capture-decran-2025-09-30-a-06.49.46.png" alt="" class="wp-image-12176"/></figure>   <strong>Figure 1a : </strong>spectres d'émission du corps noir à différentes températures   <figure class="wp-block-image size-full"><img src="https://physik.fr/wp-content/uploads/2025/09/Capture-decran-2025-09-30-a-06.49.55.png" alt="" class="wp-image-12177"/></figure>   <strong>Figure 1b : </strong>modèle du spectre d'émission du soleil.   La température de surface du Soleil peut être déterminée plus précisément à partir de la loi de Wien. Cette loi permet de déterminer la température d'un corps noir à partir de la longueur d'onde λmax de son maximum d'émission par la relation :  $

\lambda_{max}=\frac{k}{T}

$  avec :   <em>T </em>: température du corps noir, en kelvins (K) k : constante égale à 2,898×10<sup>-3</sup> m·K   5 - En considérant que le Soleil se comporte comme un corps noir, déterminer sa température de surface <em>T </em>à partir de la loi de Wien.  $

\lambda_{max}=\frac{k}{T}

$ $

T=\frac{k}{\lambda_{max}}

$ $

T=\frac{2,898 \times {10}^{-3}}{500 \times {10}^{-9}}

T=5796 K

En considérant que le Soleil se comporte comme un corps noir, à partir de la loi de Wien, on trouve que sa température de surface est T=5796 K.

Partie 3 – Énergie solaire et albedo

L’albedo est un paramètre influençant la température de surface de la Terre

6 – Définir l’albedo

L’albedo est la fraction de la lumière solaire réfléchie par une surface par rapport à la quantité totale de lumière reçue. Il varie entre 0 (aucune réflexion) et 1 (réflexion totale).

7 – Sachant que l’albedo terrestre est en moyenne égal à 0,30 et que la puissance surfacique transportée par la lumière solaire vers la surface de la Terre est en moyenne de 342 W·m^-2, calculer la puissance surfacique solaire moyenne absorbée par le sol terrestre.

P_S,absorbée=PS×(1-Albédo_Terre)

P_S,absorbée=342×(1-0,3)

P_S,absorbée=239 W.m^-2

8 – Actuellement l’albedo moyen terrestre tend à diminuer. Préciser, en justifiant votre réponse, si cette diminution conduit à une augmentation ou une diminution de la température moyenne à la surface de la Terre.

Une diminution de l’albédo terrestre conduirait à une augmentation de la puissance surfacique solaire moyenne absorbée par le sol terrestre.

Ainsi, une diminution de l’albédo terrestre conduirait à une augmentation de la température moyenne à la surface de la Terre.

Une équipe américaine a développé une peinture qui n’absorbe que 2% du rayonnement solaire.

9 – Sachant que le béton brut possède un albedo moyen égal à « 0,22 », montrer que l’utilisation de cette peinture sur les bâtiments peut contribuer à atténuer les effets du réchauffement climatique.

L’albedo mesure la fraction de la lumière solaire réfléchie par une surface. Une peinture avec un albedo de 0,98 (2% d’absorption) reflète 98% de la lumière solaire, tandis qu’un béton brut avec un albedo de 0,22 ne reflète que 22% de cette lumière.

En utilisant cette peinture, la quantité de chaleur absorbée par les bâtiments est significativement réduite. Moins de chaleur absorbée signifie une réduction de la température ambiante, atténuant ainsi les effets du réchauffement climatique.