Sujet avec enseignement de mathématiques spécifique
Enseignement scientifique première
Durée 1h12 – 12 points – Thème « La Terre, un astre singulier »
Sujet n°ENSSCIMAT156
Télécharger l’exercice en PDF :
Un adulte et un enfant regardent la mer depuis la plage. L’enfant s’interroge :
« Comment sait-on que la Terre est ronde, alors que l’horizon semble plat ? »
Document 1a – Observations dans l’Antiquité
« Quand un navire quitte la terre, sa coque est cachée en premier tandis que son mat est encore visible. »
Source : Cléomède,« Théorie des mouvements circulaires des corps célestes »,
Ier siècle av. J.-C.
Document 1b – Photographies d’un navire quittant la côte

1 – Expliquer en quoi les observations décrites dans les documents 1a et 1b permettent de justifier que la Terre n’est pas plate. On pourra s’aider d’un ou de plusieurs schémas.
Les documents 1a et 1b décrivent, le premier par un texte et le second par des images, l’observation de la différence de vision d’un navire loin et proche de la côte. La première partie du bateau à disparaître en s’éloignant est le bas du bateau, c’est-à-dire la coque. Si la Terre était plate, l’intégralité du bateau rapetisserait proportionnellement jusqu’à devenir imperceptible. Ce n’est pas ce que l’on observe, donc la Terre n’est pas plate.
2 – Donner, à l’aide de vos connaissances, une autre observation faite dans l’Antiquité confirmant l’idée d’une Terre ronde.
Une autre observation faite à l’antiquité permettant de confirmer que la terre est ronde est l’observation de l’ombre de la terre lors des éclipses de lune.
Après quelques explications, l’adulte montre à l’enfant le bateau qu’il voit à l’horizon, mais l’enfant ne le voit pas ! On cherche maintenant à expliquer pourquoi.
Document 2 – Détermination de la distance 𝒅 à l’horizon pour l’adulte
Rayon de la Terre : 𝑅 = 6371𝑘𝑚 = 6,371 × 106𝑚
Hauteur des yeux de l’adulte par rapport au niveau de la mer : ℎ = 1,75𝑚
Distance à l’horizon où se situe le bateau : 𝑑
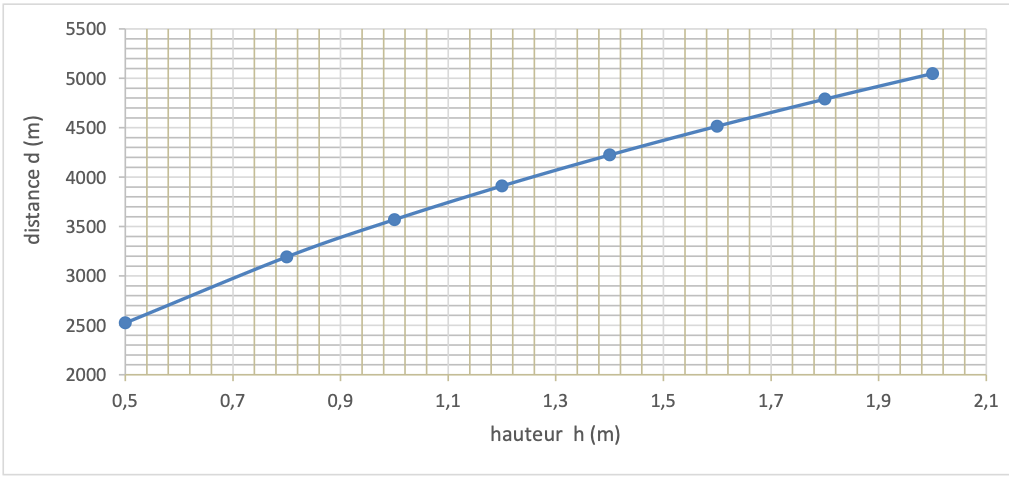
Document 3 – Distance 𝒅 à l’horizon en fonction de la hauteur 𝒉 des yeux d’un observateur au niveau de la mer
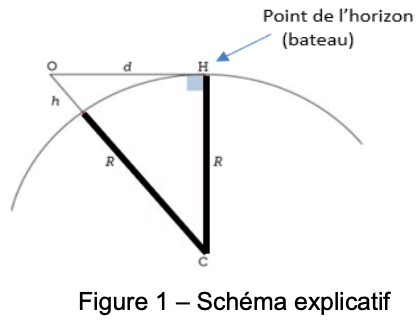
3 – En utilisant le document 2 et le théorème de Pythagore, exprimer la distance 𝑑 en fonction de 𝑅 et de ℎ puis montrer que 𝑑 peut s’écrire :
$$d=\sqrt{h \times R \times \left(2+\frac{h}{R}\right)}$$
D’après le document 2, figure 1 On observe un triangle OCH rectangle en H. On applique dans ce triangle le théorème de Pythagore.
$${\rm CO}^2={\rm OH}^2+{\rm HC}^2$$
$$\left(R+h\right)^2=d^2+R^2$$
$$d^2+R^2=\left(R+h\right)^2$$
$$d^2=\left(R+h\right)^2-R^2$$

(Identité remarquable a2-b2=( a + b)( a – b)
$$d^2=\left(R+h+R\right)\left(R+h-R\right)$$
$$d^2=\left(2R+h\right)\left(h\right)$$
$$d^2=h \times \left(2R+h\right)$$
$$d=\sqrt{h \times \left(2R+h\right)}$$
$$d=\sqrt{h \times \left(2R+h \times \frac{R}{R}\right)}$$
$$d=\sqrt{h \times R \times \left(2+\frac{h}{R}\right)}$$
On retrouve ainsi l’expression de l’énoncé.
4 – Justifier que $2+\frac{h}{R}\approx2$
$$2+\frac{h}{R}=2+\frac{1,75}{6,371 \times {10}^6}$$
$$2+\frac{h}{R}=2,000000275$$
$$2+\frac{h}{R}\approx2$$
Pour la suite de l’exercice, on admet que la distance à l’horizon s’exprime :
$$d \approx \sqrt{2 \times R \times h}$$
5 – Calculer 𝑑 et préciser si la valeur obtenue est compatible avec le document 3.
$$d\approx\sqrt{2 \times R \times h}$$
$$d\approx\sqrt{2 \times 6,371 \times {10}^6 \times 1,75}$$
$$d\approx4722\ m$$
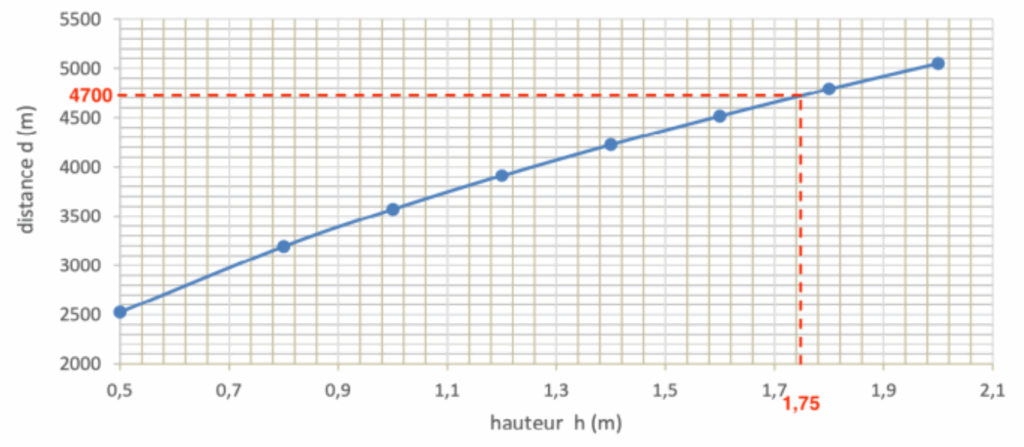
Graphiquement, sur le document 3, on a pour une hauteur de 1,75m environ une distance d de 4700m. Ainsi, la valeur obtenue est compatible avec le document 3.
6 -Justifier pourquoi l’enfant ne peut pas voir le bateau. (On estimera la hauteur ℎ de ses yeux à 1,10 m).
Soit par calcul :
$$d\approx\sqrt{2 \times R \times h}$$
$$d\approx\sqrt{2 \times 6,371 \times {10}^6 \times 1,1}$$
$$d\approx3744\ m$$
Soit graphiquement, sur le document 3, pour une hauteur h de 1,1m l’horizon se trouve, pour l’enfant à 3750m.
Le bateau est situé à 1km plus loin (voir question précédente) !
C’est pourquoi l’enfant ne peut pas voir le bateau.
