Chauffage et eau chaude de la maison

E3C2 – 10 points – Durée 1h – calculatrice autorisée

Les principales dépenses d’énergie au sein d’une maison française se répartissent entre quatre grands postes dont le plus important est le chauffage. La production d’eau chaude sanitaire est aussi un poste important.

Le but de l’exercice est d’étudier les dépenses énergétiques liées à ces deux postes (chauffage et production d’eau chaude sanitaire) dans une maison comportant deux étages.

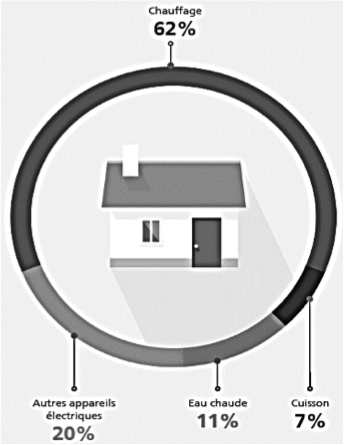
Principales dépenses d’énergie au sein d’une maison française

Source https://travaux.edf.fr/

1. Chauffage de la maison

La maison est équipée d’un chauffage central à partir d’une chaudière fonctionnant au gaz naturel. Afin de réaliser des économies d’énergie, le choix a été fait d’installer une chaudière à condensation. Le principe de fonctionnement d’une chaudière à condensation est illustré sur ci-dessous.

Dans le brûleur (1), la combustion du gaz naturel permet de transférer de l’énergie à l’eau du circuit de chauffage (2). Cette eau, après avoir alimenté les radiateurs (3), circule dans un serpentin (4) mis en contact avec les produits de la combustion du gaz naturel (5). Ces produits se condensent au contact de l’eau froide et les condensats produits dans la chaudière (6) sont ensuite rejetés à l’égout. La condensation étant un phénomène exothermique, de l’énergie thermique est ainsi fournie à l’eau du circuit de chauffage.

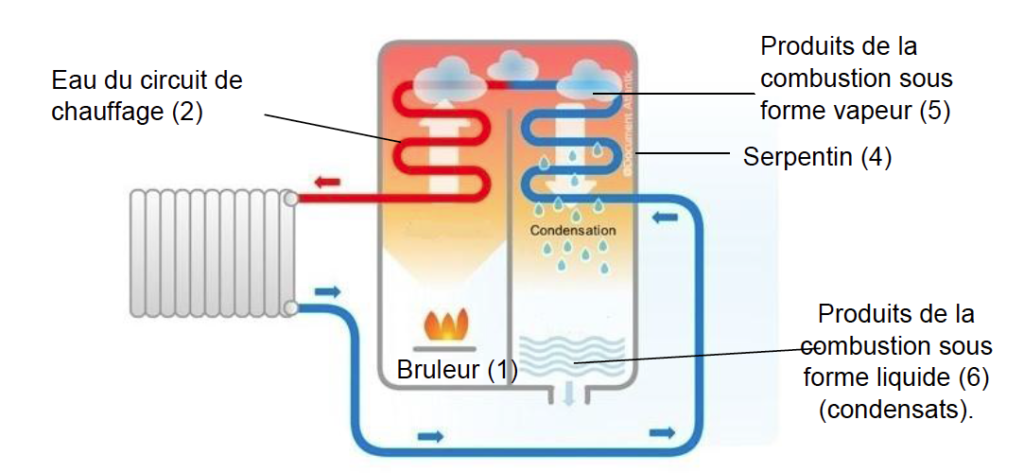
Principe de fonctionnement d’une chaudière à condensation.

D’après https://ma-maison-eco-confort.atlantic.fr/

Données :

le « gaz naturel » est principalement constitué de méthane ;
énergies molaires des liaisons en kJ·mol^-1

liaison	C-H	C=O (dans CO₂)	O=O	O-H
énergie de liaison (kJ·mol^-1)	411	795	494	459

masses molaires atomiques en g·mol^-1 : H : 1,0 g·mol^-1 ; C : 12,0 g·mol^-1 ; O : 16,0 g·mol^-1
numéros atomiques : H : 1 C : 6 O : 8 ;
la valeur de l’énergie libérée par la condensation d’un gramme d’eau est : 2,3 kJ ;
masse volumique de l’eau liquide : ρ = 1,0 kg·L^-1.

1.1. Écrire l’équation de la réaction modélisant la combustion du gaz naturel dans le dioxygène. La formule du méthane est CH₄ et les produits de combustion sont le dioxyde de carbone et l’eau.

CH₄+2O₂→CO₂+2H₂O

1.2. Établir le schéma de Lewis des molécules de dioxyde de carbone et d’eau.

₁H : 1s¹ donc 1 électron de valence

₈O : 1s²2s²2p⁴ donc 6 électrons de valence

₆C : 1s²2s²2p² donc 4 électrons de valence

H : 1 liaison

O : 2 liaisons et 2 doublets non liants

C : 4 liaisons

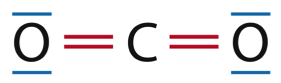
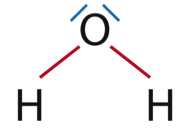
1.3. À partir du tableau donnant les valeurs des énergies de liaison, calculer celle de l’énergie molaire de réaction de la combustion du gaz naturel dans le dioxygène et justifier du caractère exothermique de la transformation. En déduire que le pouvoir calorifique du méthane est d’environ 50 kJ·g^-1.

Er = 4 E_C-H+ 2 E_O=O− 4 E_O-H− 2 E_C=O

Er = 4 × 411 + 2 × 494 − 4 × 459 − 2 × 795

Er = − 794 kJ.mol⁻¹ (exothermique car Er négatif)

Calculons la masse d’une mole de méthane :

m=n×M=1,0×(12,0+4×1,0)=16g

Pouvoir calorifique

$P_c=\frac{E_r}{m}=\frac{794}{16}=50 kJ.g^{-1}$

1.4. Calculer l’énergie thermique libérée au cours de la combustion de 100 g de méthane. Montrer qu’au cours de cette combustion il se forme 225 g de vapeur d’eau.

$P_c=\frac{E_r}{m}$

$E_r=m \times P_c = 100 \times 50 = 5,0.10^3 KJ$

Calculons les quantités de matière des réactifs :

$n_{méthane}^i=\frac{m_{méthane}}{M_{méthane}}$

$n_{méthane}^i=\frac{100}{12,0+4 \times 1,0}=6,25 mol$

$n_{dioxygène}^i=excés$

Equation		CH₄	+ 2O₂	→ CO₂	+ 2H₂O
Etat initial	x=0mol	6,25	excès	0	0
Etat intermédiaire	x	6,25-x	excès	x	2x
Etat final	x=x_f	6,25- x_f	excès	x_f	2x_f

Calculons x_max :

6,25- x_max =0

x_max =6,25 mol

$n_{eau}={n_{eau}^f}\times {M_{eau}}$

$n_{eau}={2 x_{max}}\times {M_{eau}}$

$n_{eau}=2 \times 6,25 \times (2\times1,0 +16,0) = 225 g$

1.5. On fait l’hypothèse que toute la vapeur d’eau formée lors de la combustion se condense et que seule l’énergie libérée lors de la condensation de l’eau est récupérée. Calculer la valeur de l’énergie associée à la condensation de la vapeur d’eau formée pour 100 g de méthane puis montrer que l’utilisation de cette énergie permet de réaliser un gain maximal d’environ 10 % en énergie.

La valeur de l’énergie libérée par la condensation d’un gramme d’eau est : 2,3 kJ ;

Pour 225 g d’eau (combustion de 100 g de méthane): E=225×2,3=518kJ

L’énergie thermique libérée au cours de la combustion (question 1.4) : Er=5,0.10³kJ

Calculons le pourcentage :

$P=\frac{E}{Er}\times 100=\frac{518}{5,0.10^3}\times 100=10\%$

2. Eau chaude sanitaire

Dans ce logement l’eau chaude sanitaire est fournie par chauffe-eau qui fonctionne à l’électricité. Le principe est simple : une résistance électrique placée dans le cumulus chauffe l’eau jusqu’à une température définie appelée température de consigne.

Les caractéristiques techniques du chauffe-eau indiquées par le constructeur sont en partie reproduites :

Capacité	Tension de fonctionnement	Puissance	Temps de chauffe⁽¹⁾
150 L	230 V	1800 W	5 h 15

(1) Le temps de chauffe est indiqué pour une eau dont la température initiale est de 15 °C et la température finale de 65 °C.

Données :

L’énergie thermique E nécessaire pour élever la température d’une masse m d’eau liquide de ΔT est donnée par la relation E = m·c_eau·ΔT où c_eau est la capacité thermique massique de l’eau (c_eau = 4,18×10³J·kg^-1·K^-1) ;
masse volumique de l’eau ρ = 1,00 kg·L^-1;
ϴ(°C) = T(K) – 273 ; 1,0 J = 3,6kWh ;1 bar = 10⁵ Pa.

2.1. Nommer le phénomène physique qui permet le chauffage de l’eau dans le cumulus. Déterminer la valeur de la résistance chauffante du cumulus.

Une résistance électrique placée dans le cumulus chauffe l’eau : c’est l’effet joule.

D’après la loi d’ohm : U=R.I Donc

$R=\frac{U}{I}$

Or : P=U.I d’ou

$\ I=\frac{P}{U}$

d’ou

$R=\frac{U}{P/U}=\frac{U^2}{P}=\frac{230^2}{1800}=29\Omega$

2.2. À l’aide des caractéristiques techniques du constructeur et des données, calculer la valeur de l’énergie thermique nécessaire à l’élévation de la température de la totalité de l’eau du cumulus.

E = m·c_eau·ΔT

$\rho =\frac{m}{V}$

d’ou m= ρ×V

Donc :

E = ρ×V×c_eau×ΔT

E = 1,0×150×4,18×10³×(65-15)=3,1.10⁷J

2.3. Utiliser la puissance du chauffe-eau pour en déduire la durée nécessaire à cette élévation de température. Comparer à la valeur indiquée par le constructeur et proposer une explication à une éventuelle différence.

$P =\frac{E}{\Delta t}$

$\Delta t =\frac{E}{P}$

$\Delta t =\frac{3,1.10^7}{1800}=1,7.10^4 s =4 h 43 min$

D’après la notice le temps de chauffe est 5 h 15

Cette différence peux s’expliquer par :

Une eau à une température initiale plus basse que 15°C
Des pertes énergétiques dues à une mauvaise isolation du chauffe eau

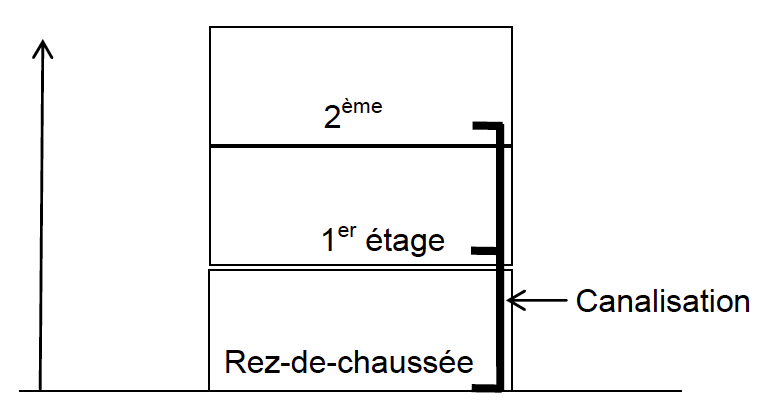
Le cumulus est installé au rez-de-chaussée d’une maison de deux étages (schéma ci-contre). Le graphe ci-dessous indique la pression minimale de l’eau en sortie du cumulus en fonction de l’altitude z du point de distribution de l’eau chaude. Pour un fonctionnement correct l’eau doit arriver au point de distribution avec une pression minimale de 2,50 bar.

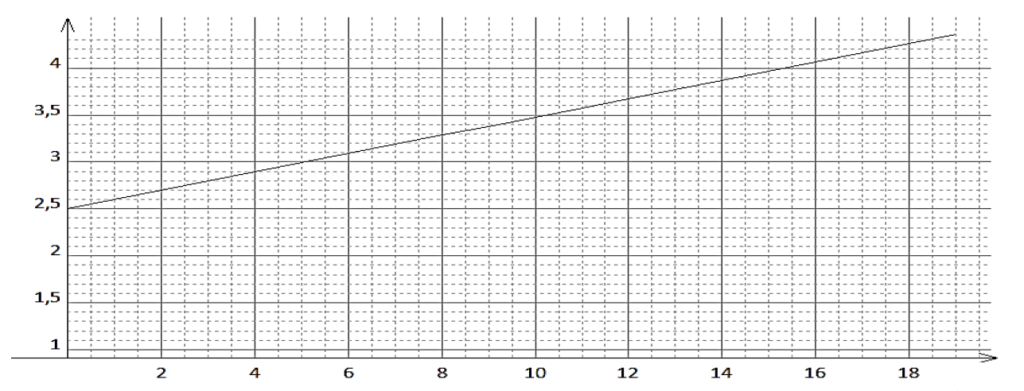
Pression de l’eau en sortie de cumulus en fonction de l’altitude de la distribution

2.4. Commenter l’allure du graphe puis l’utiliser pour estimer la pression minimale de l’eau en sortie du cumulus nécessaire à la distribution d’eau chaude dans une maison de deux étages.

Nous avons une fonction affine :

La pression minimale de l’eau en sortie du cumulus est croissante en fonction de l’altitude z.

Un étage mesure environs 3m soit 6m pour 2 étages.

Par lecture graphique pour Z=6m, P=3,1 bar

La pression minimale de l’eau en sortie du cumulus doit être de 3,1 bar