Cloche de plongée

E3C2 – 10 points – Durée 1h – calculatrice autorisée

À partir du 16e siècle, les hommes commencent à s’intéresser à la récupération d’épaves et notamment aux trésors qu’elles renferment. Ils imaginent de nouvelles techniques pour respirer sous l’eau tout en résistant à la pression. Parmi les engins inventés : la cloche de plongée.

Il s’agit d’un simple tonneau ouvert vers le bas et lourdement lesté, pouvant contenir plusieurs plongeurs. Elle est descendue à la verticale et posée sur ou près du fond.

En 1690, le physicien anglais Edmund HALLEY, qui a également découvert la célèbre comète de Halley, améliore le principe de la cloche de plongée.

Elle est actuellement encore utilisée pour véhiculer du matériel et du personnel entre la surface et des zones de travail subaquatiques.

On modélise une cloche de plongée par un cylindre sans plancher dont la surface de la base S est égale à 1,0 m² et la hauteur H à 2,4 m.

Avant d’être immergée dans l’eau, la cloche est entièrement remplie d’air à la pression atmosphérique p_atm = 1,013×10⁵ Pa. On considère que la quantité d’air, ainsi que la température, restent constantes au cours de l’immersion de la cloche.

Données :

masse volumique de l’eau de mer dans laquelle la cloche est immergée :ρ =1,02×10³ kg.m^-3;
intensité de la pesanteur : g = 9,81 m.s^-2.

Étude expérimentale de la loi de Mariotte

Pour modéliser le comportement de l’air dans la cloche, on utilise le matériel photographié ci-contre. La pression P de l’air emprisonné dans la seringue est relevée pour différentes valeurs du volume V du corps de la seringue. On suppose que la température de l’air reste constante.

Les résultats obtenus sont rassemblés dans le tableau ci-dessous :

P (hPa)	1011	1127	1261	1419	1633	1932
V (cm³)	50	45	40	35	30	25

1.1. Quelle précaution doit-on prendre pour s’assurer que la température de l’air reste la même lors de chaque mesure ?

Pour s’assurer que la température de l’air reste la même lors de chaque mesure, Il faudra :

ne pas maintenir le corps de la seringue à pleines mains
ne pas déplacer le piston trop rapidement.

1.2. Énoncer la loi de Mariotte relative au produit de la pression P par le volume V d’un gaz pour une quantité de matière donnée et une température constante.

Loi de Mariotte : pour une quantité de gaz constante, à une température constante le produit de la pression P et du volume V est constant :

P.V=Constante

1.3. On utilise un programme écrit en langage Python pour tracer la courbe donnant la pression P en fonction de l’inverse du volume V. Un extrait de ce programme est donné ci-après.

pression = [1011,1127,1261,1419,1633,1932]

volume = [25,30,35,40,45,50]

invVolume = [ ]

pyplot.axis([0,0.05,0,2000])

pyplot.xlabel(‘’ 1/V (mL-1)’’)

pyplot.ylabel(‘’p (hPa) »)

pyplot.title(‘’Etude de la loi de Mariotte »)

for i in range (0,6) :

invVolume.append(1/volume[i])

pyplot.scatter (invVolume,pression,color=’black’,marker=‘’+”)

pyplot.show ( )

Le tracé obtenu suite à l’exécution du programme est reproduit ci-après :

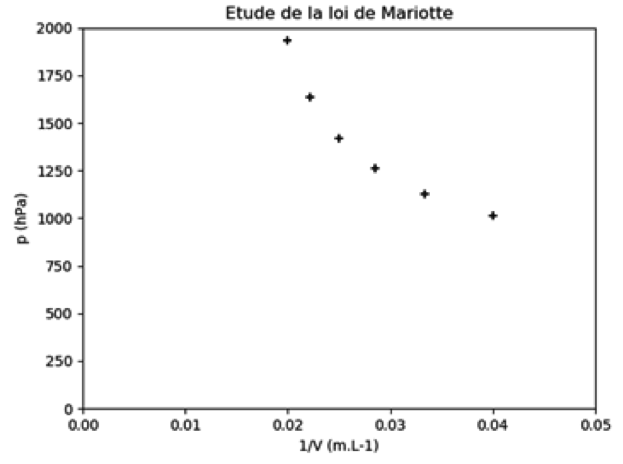
1.3.1. La courbe obtenue est-elle cohérente avec la loi de Mariotte ? Justifier.

Loi de Mariotte : P.V=Constante

$P=\frac{constante}{V}$

$P=constante \times \frac{1}{V}$

P est proportionnel à 1/V. La courbe P=f(1/V) doit être une droite passant par l’origine.

La courbe obtenue n’est pas cohérente avec la loi de Mariotte.

1.3.2. Identifier l’erreur commise dans le programme.

Les volumes et pressions ne correspondent pas. Il faut les mettre dans le même ordre.

pression = [1011,1127,1261,1419,1633,1932]

~~volume = [25,30,35,40,45,50]~~ volume = [50,45,40,35,30,25]

1.4. Exploiter, par une méthode au choix, les résultats expérimentaux obtenus afin de tester la loi de Mariotte.

1^ère méthode :

On calcule le produit PV pour chaque mesure :

P (hPa)	1011	1127	1261	1419	1633	1932
V (cm³)	50	45	40	35	30	25
PV (hPa.cm³)	5,1.10⁴	5,1.10⁴	5,0.10⁴	5,0.10⁴	4,9.10⁴	4,8.10⁴

Le produit PV est pratiquement constant.

2^nd méthode :

On trace le graphique P=f(1/V)

P (hPa)	1011	1127	1261	1419	1633	1932
V (cm³)	50	45	40	35	30	25
1/V (cm^-3)	0,020	0,022	0,025	0,029	0,033	0,040

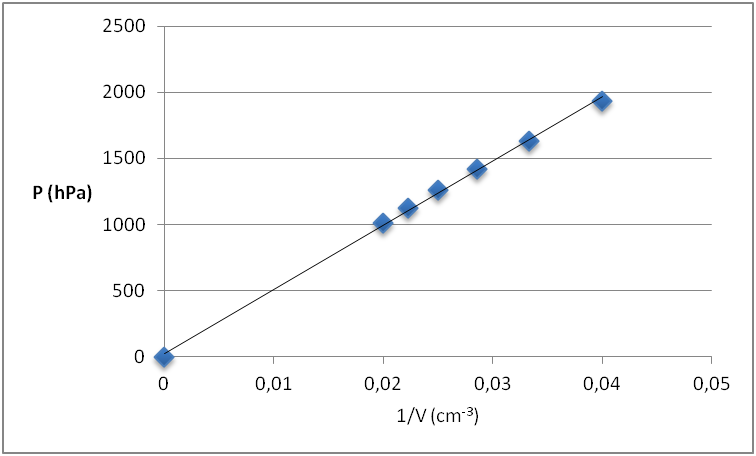
On obtient une droite passant par l’origine.

2. Fonctionnement de la cloche de plongée

2.1. Force pressante exercée par l’eau de mer sur la surface horizontale supérieure de la cloche immergée à 18 m de profondeur.

2.1.1. La loi fondamentale de la statique des fluides reliant la différence de pression p_A – p_B entre deux points A et B d’un fluide incompressible à ρ, g, et z_B – z_A ,s’écrit p_A – p_B = ρ.g.(z_B – z_A) ; z_A et z_B étant les ordonnées des points A et B sur un axe des z orienté suivant la verticale ascendant. Décrire, en le justifiant, l’évolution de la pression en fonction de la profondeur.

D’après la loi fondamentale de la statique des fluides : p_A – p_B = ρ_e g (z_B – z_A)

Soit z_A>z_B

p_B = p_A – ρ_e g (z_B – z_A)

Or z_A>z_B

d’ou (z_B – z_A)<0

ρ_e g (z_B – z_A) <0

– ρ_e g (z_B – z_A) >0

d’ou p_B > p_A

La pression augmente lorsque le plongeur descend dans la fosse de plongée

2.1.2. Montrer que la pression p₁₈ de l’eau de mer à 18 m de profondeur est égale à 2,8×10⁵ Pa.

p_A – p_B = r.g.(z_B – z_A)

p₁₈– p_atm = r.g.(z_atm – z₁₈)

p₁₈ = r.g.( z_atm – z₁₈) + p_atm

p₁₈ = 1,02´10³×9,81× (0– (-18)) + 1,013×10⁵

p₁₈ =2,81´10⁵ Pa

2.1.3. En déduire la valeur de la force pressante F qui modélise l’action exercée par l’eau de mer sur la surface horizontale supérieure d’aire S de la cloche immergée à 18 m de profondeur.

F=P×S

F=2,81´10⁵ ×1,0

F=2,81×10⁵ N

2.1.4. Montrer que la valeur de cette force pressante est égale à celle du poids d’une masse environ égale à 29 t. Commenter.

P=mxg

P=29 x10³ ´9,81

P=2,84×10⁵ N

F≈P

Cette force pressante est donc égale à celle du poids d’une masse environ égale à 29 t

Il faut donc que la cloche résiste à des forces très importantes.

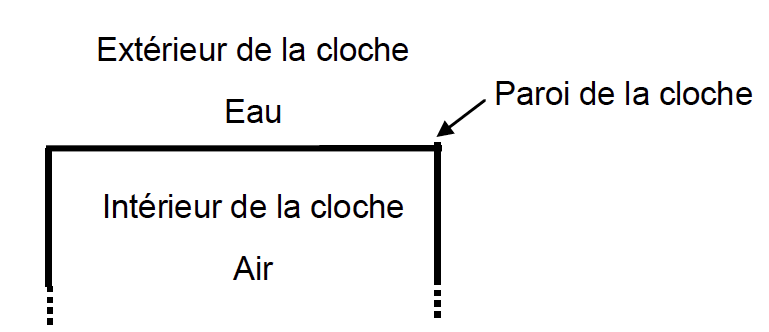
2.2. En comparant qualitativement la pression de l’air dans la cloche immergée et la pression atmosphérique, expliquer pourquoi le niveau de l’eau à l’intérieur de la cloche augmente lorsque celle-ci est immergée.

On considère que la quantité d’air, ainsi que la température, restent constantes au cours de l’immersion de la cloche.

$V_{immergée} \times P_{immergée}=P_{atmosphérique}\times V_{atmosphérique}$

$V_{immergée}=\frac{(P_{atmosphérique}\times V_{atmosphérique})}{P_{immergée}}$

La pression de l’air dans la cloche immergée est supérieure à la pression atmosphérique. Donc V_immergée<V_{atmosphérique}

2.3. On néglige la variation de la pression de l’eau sur la hauteur de la cloche.

2.3.1. Déterminer la valeur du volume d’air V₀ contenu initialement dans la cloche cylindrique de section S et de hauteur H.

V₀=SxH

V₀=1,0×2,4=2,4m³

2.3.2. Déterminer, en utilisant la loi de Mariotte, le volume V₁₈d’air contenu dans la cloche à 18 m de profondeur.

$V_{18} \times P_{18}=P_{atm}\times V_{0}$

$V_{18}=\frac{(P_{atm}\times V_{0})}{P_{18}}$

$V_{18}=\frac{1,02\times 10^5 \times 2,4}{2,81 \times 10^5}=0,87 m^3$

2.3.3. En déduire de quelle hauteur h₁₈ est montée l’eau dans la cloche.

V₁₈=S×H’

H’=V₁₈/S

H’=0,87/1,0=0,87 m

Or h₁₈=H-H’

h₁₈=2,4-0,87=1,53 m