Sujet avec enseignement de mathématiques spécifique
Enseignement scientifique première
Durée 1h12 – 12 points – Thème « Une longue histoire de la matière »
Sujet n°
Télécharger l’exercice en PDF :
Ötzi est une momie naturelle retrouvée dans les Alpes il y a 30 ans, allongée à plat ventre, au bord d’un lac gelé situé à 3 000 mètres d’altitude dans la vallée d’Ötzal.
Les analyses scientifiques ont révélé qu’il s’agit d’une très ancienne scène de crime…

Découverte de la momie et reconstitution de Ötzi, musée archéologique de Haut-Adige
Crédit photo : SOUTH TYROL MUSEUM OF ARCHAEOLOGY.
L’objectif de cet exercice est d’estimer la date de l’assassinat d’Ötzi.
Partie 1 – L’atome de carbone
Document 1 – Origine et cycle du carbone 14C
Le carbone présent dans l’atmosphère essentiellement sous forme de dioxyde de carbone (CO2) possède plusieurs isotopes : carbone 12, carbone 13, carbone 14.
Le carbone 14 est un isotope radioactif du carbone donc instable ; il se désintègre spontanément en un noyau fils (azote 14) plus stable.
Sa période radioactive (ou « demi-vie ») est de 5 730 ans.
On peut considérer que tant qu’une plante ou un animal est vivant, son organisme échange du carbone avec son environnement, si bien que le carbone qu’il contient aura la même proportion de 14C (carbone 14) que dans la biosphère.
Lorsque cet organisme meurt, son métabolisme cesse, il ne reçoit plus
de carbone 14 et celui qu’il contient va se désintégrer peu à peu au cours du temps selon une loi exponentielle.
La datation par le carbone 14 se fonde alors sur le comptage du carbone 14 résiduel dans l’organisme mort.
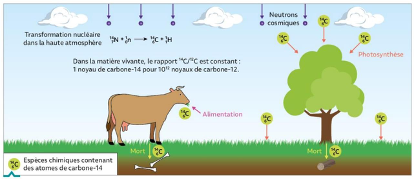
Figure A – Cycle du Carbone 14
Source : Manuel Nathan 1ère Enseignement Scientifique
À l’aide des informations du document 1 :
1- Donner la caractéristique d’un isotope radioactif.
Un isotope radioactif est instable ; il se désintègre spontanément en un noyau fils plus stable.
2 – Expliquer pourquoi le carbone 14 n’est plus renouvelé à la mort des êtres vivants.
Le carbone 14 est un isotope radioactif du carbone qui est produit dans l’atmosphère terrestre. Ce carbone 14 est se retrouve dans le dioxyde de carbone qui est absorbé par les plantes lors de la photosynthèse. Les animaux se nourrissent de plantes ou d’autres animaux. Ainsi, tout au long de leur vie, les plantes et les animaux maintiennent un équilibre relatif entre la quantité de carbone 14 qu’ils absorbent et celle qu’ils perdent.
A la mort d’un organisme, les échanges avec l’environnement cessent. Par conséquent, le carbone 14 présent dans l’organisme ne se renouvelle plus.
3 – Énoncer ce qu’il faut quantifier pour évaluer la date de la mort d’un être vivant.
Justifier votre réponse.
À partir de la mort d’un être vivant, le carbone 14 commence à se désintégrer car il n’est plus remplacé par du carbone 14 provenant de l’environnement.
En mesurant la quantité de carbone 14 restant dans un échantillon et en la comparant avec la quantité de carbone 14 dans un être vivant, on peut estimer depuis combien de temps l’organisme est mort.
Ainsi, pour évaluer la date de la mort d’un être vivant, il faut quantifier sa teneur en carbone 14.
4 – Énumérer la succession des évènements qui aboutissent à la présence de carbone 14 dans le corps d’Ötzi.
La succession des évènements qui aboutissent à la présence de carbone 14 dans le corps d’Ötzi sont :
- La création du carbone 14 par transformation nucléaire dans la haute atmosphère.
- Insertion du carbone 14 dans le dioxyde de carbone
- L’absorption du carbone 14 par les plantes grâce à la photosynthèse
- Consommation alimentaire d’Ötzi
Partie 2 – Datation d’une mort
À la mort d’Ötzi, le nombre initial 𝑁0 de noyaux de carbone 14 contenu dans son corps était de 3,87 × 1015.
À la découverte de la momie, elle possédait une activité radioactive en carbone 14 de :
𝐴 = 7910 Bq
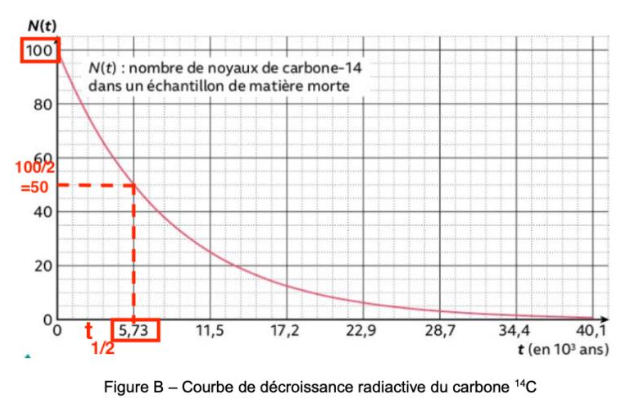
5 – Établir la valeur de la demi-vie du carbone 14, en utilisant le graphique du document 3 (page suivante) et en exposant la démarche permettant de la déterminer.
La demi-vie est le temps au bout duquel la moitié des noyaux radioactifs initialement présents se sont désintégrés.
Graphiquement : t1/2=5,73×103 ans
6 – À l’aide des informations du document 2 (ci-après), calculer le nombre N de noyaux résiduels dans la momie au moment de sa découverte.
D’après le document 2 : Ainsi l’activité 𝐴 en Bq de cet échantillon et le nombre de noyaux N qu’il contient sont liés par la relation (𝑡1/2 : demi-vie de l’échantillon radioactif exprimée en seconde) :
$$N=\frac{A \times t_{1/2}}{0,69}$$
Calculons le nombre N de noyaux résiduels dans la momie au moment de sa découverte :
$$N=\frac{A \times t_{1/2}}{0,69}$$
$$N=\frac{7910 \times 1,81 \times {10}^{11}}{0,69}$$
$$N=2,07 \times {10}^{15}$$
Au moment de sa découverte, il y a 2,07×1015 noyaux résiduels de carbone 14 dans la momie.
7 – Sachant que 3,87 × 1015 noyaux correspondent à 100 % de noyaux de carbone 14, vérifier que le pourcentage de carbone 14 résiduel lors de la découverte de la momie est de 53 %.
$$P=\frac{N}{N_{initial}}$$
$$P=\frac{2,07 \times {10}^{15}}{3,87 \times {10}^{15}}$$
P=0,53
P=53 %
Ainsi, le pourcentage de carbone 14 résiduel lors de la découverte de la momie est de 53 %.
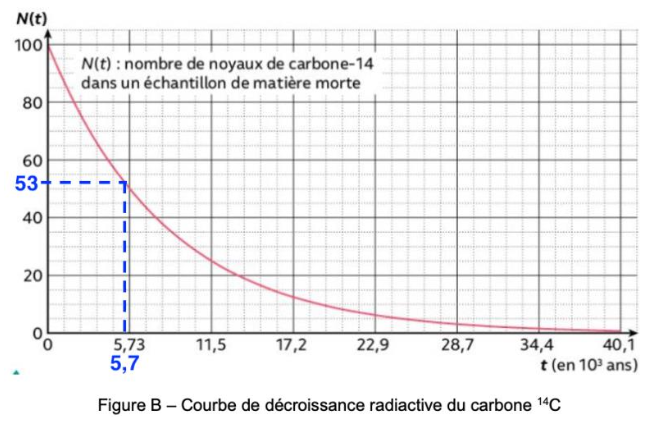
8 – À l’aide du résultat de la question précédente et de la courbe de décroissance radioactive du carbone 14, estimer la date de l’assassinat d’Ötzi.
Graphiquement, pour 53% de de carbone 14 résiduel, il s’est écoulé environs 5,7×103 ans soit 5700 ans.
Nous sommes en 2024 (date de la correction de ce sujet, a adapté pour les prochaines années) et Ötzi est une momie naturelle retrouvée dans les Alpes il y a 30 ans :
La date de l’assassinat d’Ötzi est estimée en -3706 avant JC.
Document 2 – Définition de l’activité d’un échantillon
On appelle activité 𝐴 d’un échantillon radioactif le nombre de désintégrations de noyaux qui s’y produisent par seconde. Ainsi l’activité 𝐴 en Bq de cet échantillon et le nombre de noyaux N qu’il contient sont liés par la relation :
$$N=\frac{A\timest_{1/2}}{0,69}$$
𝑡1/2 : demi-vie de l’échantillon radioactif exprimée en seconde.
Données :
- 5730 ans = 1,81 × 1011 secondes.
Document 3 – Courbe de décroissance radioactive
La courbe de décroissance radioactive du carbone 14 suivante montre l’évolution de la quantité de carbone 14 au cours du temps à partir de la mort d’un organisme.
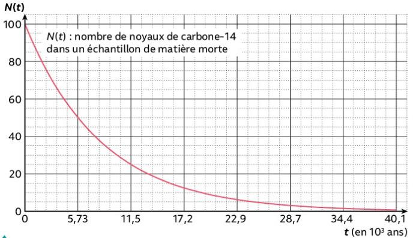
Figure B – Courbe de décroissance radiactive du carbone 14C
Source : Manuel Nathan 1ère Enseignement Scientifique
