Températures de surface de quelques objets du système solaire

Sujet sans enseignement de mathématiques spécifique

Enseignement scientifique première

Durée 1h – 10 points – Thème « Le Soleil, notre source d’énergie »

Le système solaire est formé d’une étoile, le Soleil, autour de laquelle des planètes, des satellites, des astéroïdes sont en orbite. La distance entre ces objets et l’étoile a une influence sur leur température de surface mais il semble que cela ne soit pas le seul facteur entrant en jeu…

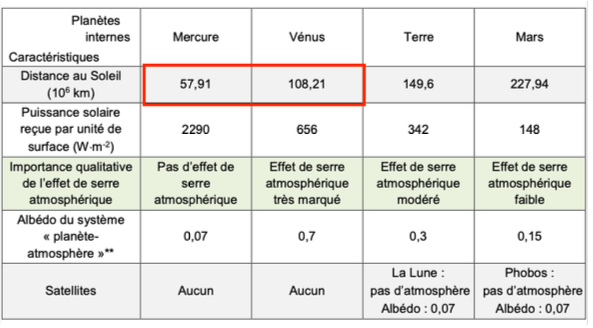
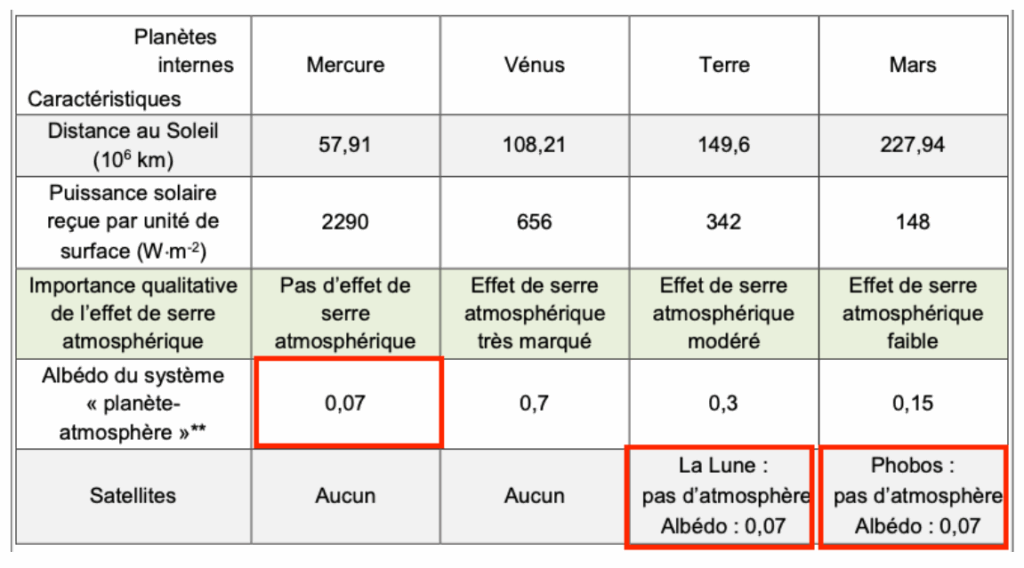
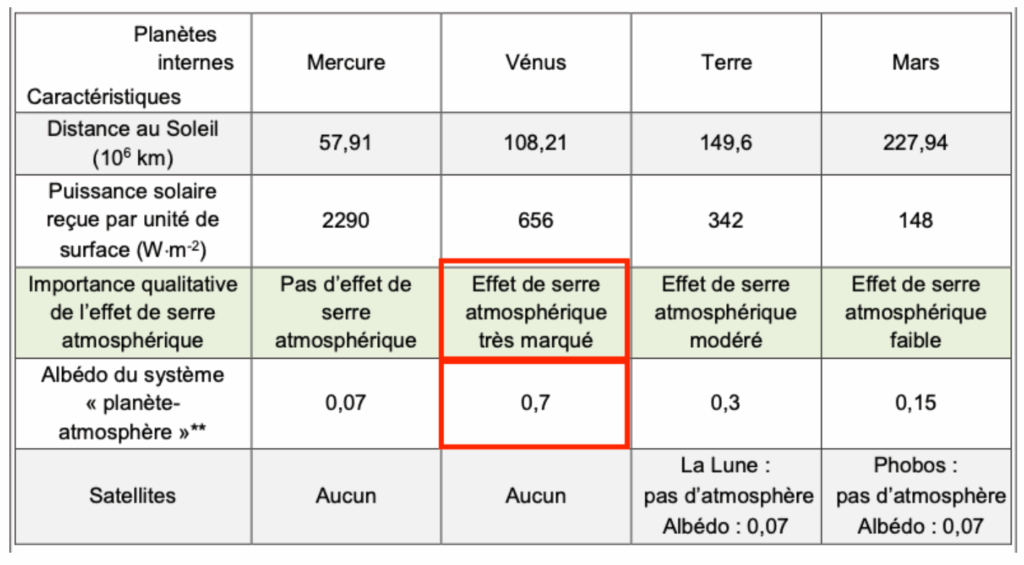
Document de référence : caractéristiques de quelques objets du système solaire
Planètes internes Caractéristiques	Mercure	Vénus	Terre	Mars
Distance au Soleil (10⁶ km)	57,91	108,21	149,6	227,94
Puissance solaire reçue par unité de surface (W×m^-2)	2290	656	342	148
Importance qualitative de l’effet de serre atmosphérique	Pas d’effet de serre atmosphérique	Effet de serre atmosphérique très marqué	Effet de serre atmosphérique modéré	Effet de serre atmosphérique faible
Albédo du système « planète- atmosphère »**	0,07	0,7	0,3	0,15
Satellites	Aucun	Aucun	La Lune : pas d’atmosphère Albédo : 0,07	Phobos : pas d’atmosphère Albédo : 0,07
** L’albédo mesure le pouvoir réfléchissant d’une surface. C’est la proportion d’énergie lumineuse réfléchie. Sa valeur est comprise entre 0 et 1. Plus une surface est réfléchissante, plus son albédo est élevé. Par exemple, l’albédo de la neige fraîche est de 0,87, ce qui signifie que 87 % de l’énergie lumineuse est réfléchie par ce type de neige. L’albédo d’un système planète-atmosphère est la proportion de l’énergie solaire qui est réfléchie par la planète et son atmosphère vers l’espace. Les éléments qui contribuent le plus à l’albédo du système Terre-atmosphère sont les nuages, les surfaces de neige et de glace et les aérosols. Source : d’après Géosciences La dynamique du système Terre de Christian Robert et Romain Bousquet, https://www.actu–environnement.com et https://www.futura-sciences.com

Partie 1 – Des données expérimentales à un modèle mathématique possible

Document 1 – Montage expérimental permettant de mesurer la puissance lumineuse reçue par un récepteur en fonction de la distance à la source lumineuse

On dispose d’une lampe et d’un capteur, le luxmètre*, permettant de mesurer l’éclairement lumineux reçu.

L’expérimentateur réalise une série de mesures en éloignant progressivement le luxmètre de la lampe. On présente ces mesures dans le tableau ci- dessous.

Tableau des mesures réalisées :

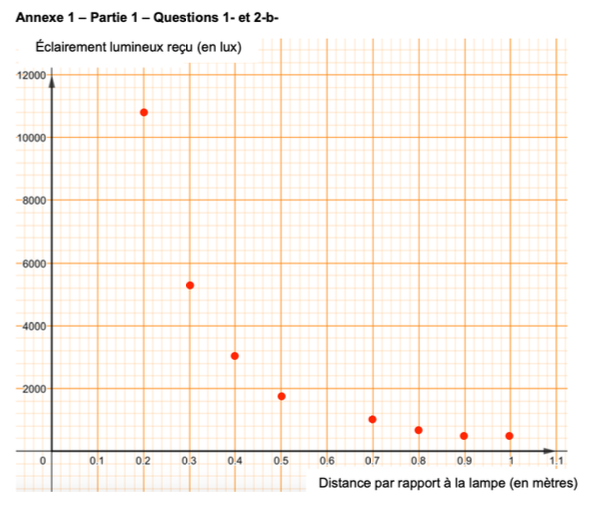
Distance par rapport à la lampe (en mètres)	0,2	0,3	0,4	0,5	0,7	0,8	0,9	1
Éclairement lumineux reçu (en lux**)	10 800	5 300	3 100	1 800	1 000	700	500	400

* Luxmètre : appareil de mesure de l’éclairement lumineux comportant une cellule photosensible.

** Lux : unité de mesure de l’éclairement lumineux (puissance lumineuse reçue par unité de surface).

Source : d’après https://www.pierron.fr/news/fiches-tp-svt-2nd.html

1 – Le graphique de l’annexe 1 (à rendre avec la copie) permet de représenter les variations de l’éclairement lumineux reçu par le capteur en fonction de la distance à la source d’énergie. Reporter sur ce graphique les points expérimentaux obtenus dans le document 1.

2 – À partir de l’allure du nuage de points obtenu à la question 1, un tableur permet de proposer une modélisation mathématique par une fonction. Cette fonction, notée 𝑓, est définie par

$f\left(d\right)=\frac{432}{d^2}$

où 𝑑 représente la distance à la lampe (en mètres) et 𝑓(𝑑) l’éclairement lumineux reçu (en lux).

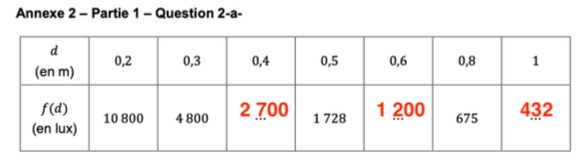
2-a- En utilisant cette modélisation mathématique, compléter le tableau de valeurs donné en annexe 2 à rendre avec la copie. On arrondira les résultats à l’unité.

$f\left(d\right)=\frac{432}{d^2}$

$f\left(d=0,4\right)=\frac{432}{{0,4}^2}$

$f\left(d=0,4\right)=2700$

$f\left(d=0,6\right)=\frac{432}{{0,6}^2}$

$f\left(d=0,6\right)=1200$

$f\left(d=1\right)=\frac{432}{1^2}$

$f\left(d=1\right)=432$

2-b- Représenter la fonction 𝑓 dans le repère donné en annexe 1.

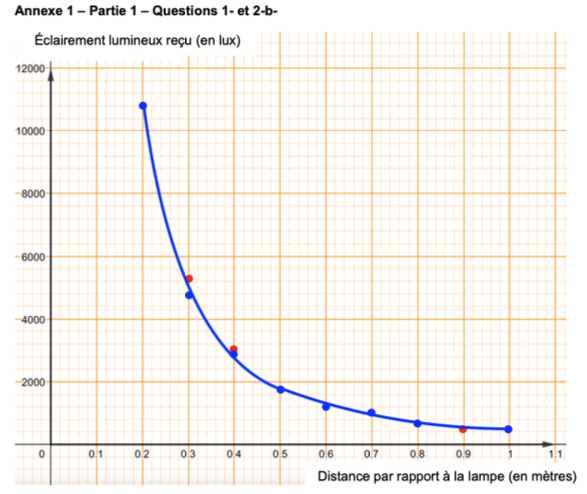
2-c- Cette modélisation mathématique semble-t-elle pertinente pour caractériser la relation entre l’éclairement lumineux reçu par le capteur et la distance à la source lumineuse ? Justifier.

Les points expérimentaux sont très proches de la courbe théorique, indiquant que cette modélisation mathématique est pertinente pour caractériser la relation entre l’éclairement lumineux reçu par le capteur et la distance à la source lumineuse.

3 – On admet que la loi illustrée expérimentalement dans le document 1 est générale :
« La puissance lumineuse par unité de surface reçue par un objet est inversement proportionnelle au carré de la distance qui le sépare de la source lumineuse ».
En s’appuyant sur le document de référence, choisir, parmi les affirmations suivantes, celle qui est correcte au regard de ce modèle. L’écrire sur la copie et justifier la réponse donnée.

La puissance lumineuse par unité de surface, provenant du Soleil et reçue sur Vénus est environ :
a) deux fois plus grande que celle reçue sur Mercure ;
b) quatre fois plus grande que celle reçue sur Terre ;
c) deux fois plus petite que celle reçue sur Terre ;
d) quatre fois plus petite que celle reçue sur Mercure.

« La puissance lumineuse par unité de surface reçue par un objet est inversement proportionnelle au carré de la distance qui le sépare de la source lumineuse ».

proportionnelle : k
inversement : 1/x
carré de la distance : d²

inversement proportionnelle au carré de la distance : k x 1/d².

La distance Soleil-Venus est environs deux fois plus grande que la distance Soleil-Mercure.

Comme la puissance lumineuse par unité de surface reçue par un objet est inversement proportionnelle au carré de la distance qui le sépare de la source lumineuse : P= k x 1/d².

d est au carré, donc 2²=4 et comme elle est inversement proportionnel ¼.

Ainsi, la puissance lumineuse par unité de surface, provenant du Soleil et reçue sur Vénus est environ :

~~a) deux fois plus grande que celle reçue sur Mercure ;~~

~~b) quatre fois plus grande que celle reçue sur Terre ;~~

~~c) deux fois plus petite que celle reçue sur Terre ;~~

d) quatre fois plus petite que celle reçue sur Mercure.

Partie 2 – Confrontation du modèle mathématique à la réalité

Dans cette partie, on admet que la puissance reçue par unité de surface par les objets du système solaire est inversement proportionnelle au carré de leur distance au soleil, d’une façon analogue à l’étude menée en partie 1. Moyennant certaines hypothèses, on peut en déduire une « loi de variation de la température moyenne des planètes en fonction de leur distance au soleil » (voir le document 2).

Document 2 – Températures de surface de quelques objets proches du Soleil

Le graphique ci-dessous précise :

Les températures moyennes effectivement mesurées à la surface de différentes planètes en fonction de leur distance au soleil (points gris) ;
L’évolution de la température moyenne d’un objet en fonction de la distance au soleil modélisée par la « loi de variation de la température moyenne des planètes en fonction de leur distance au soleil » (courbe continue).

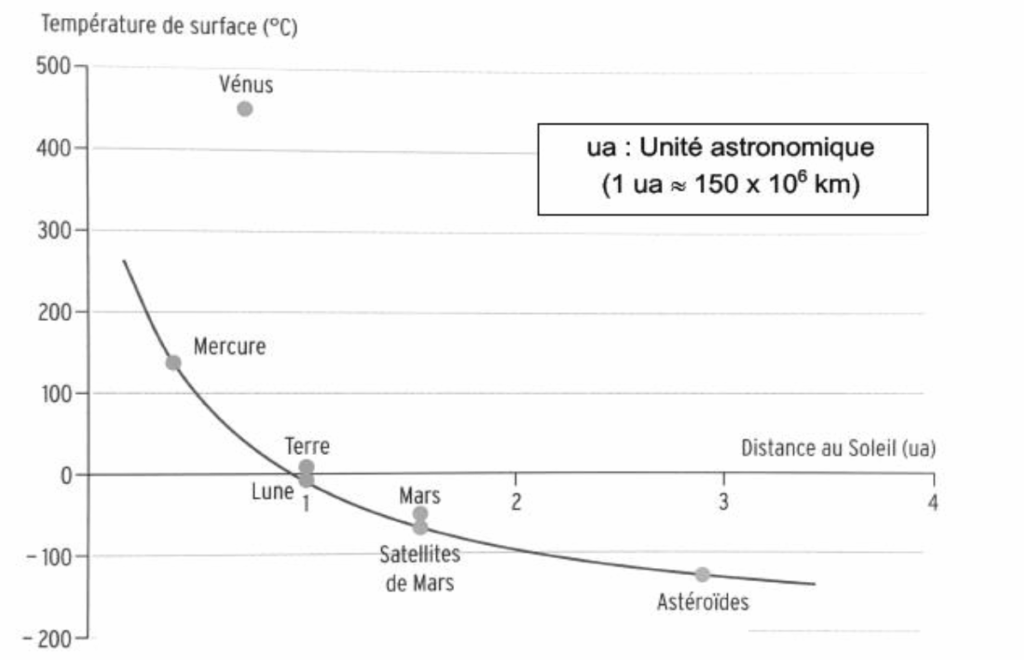
Source : Collection in vivo, SVT 2^de 2004, Magnard

4 – Quels sont les objets considérés dans le document 2 pour lesquels la loi modélisant l’évolution de la température des planètes en fonction de leur distance au Soleil est bien vérifiée ? Quelles propriétés ces objets ont-ils en commun ?

Les objets considérés dans le document 2 pour lesquels la loi modélisant l’évolution de la température des planètes en fonction de leur distance au Soleil est bien vérifiée, sont ceux qui sont sur la courbe soit :

Mercure
La lune
Les satellites de Mars
Les astéroïdes.

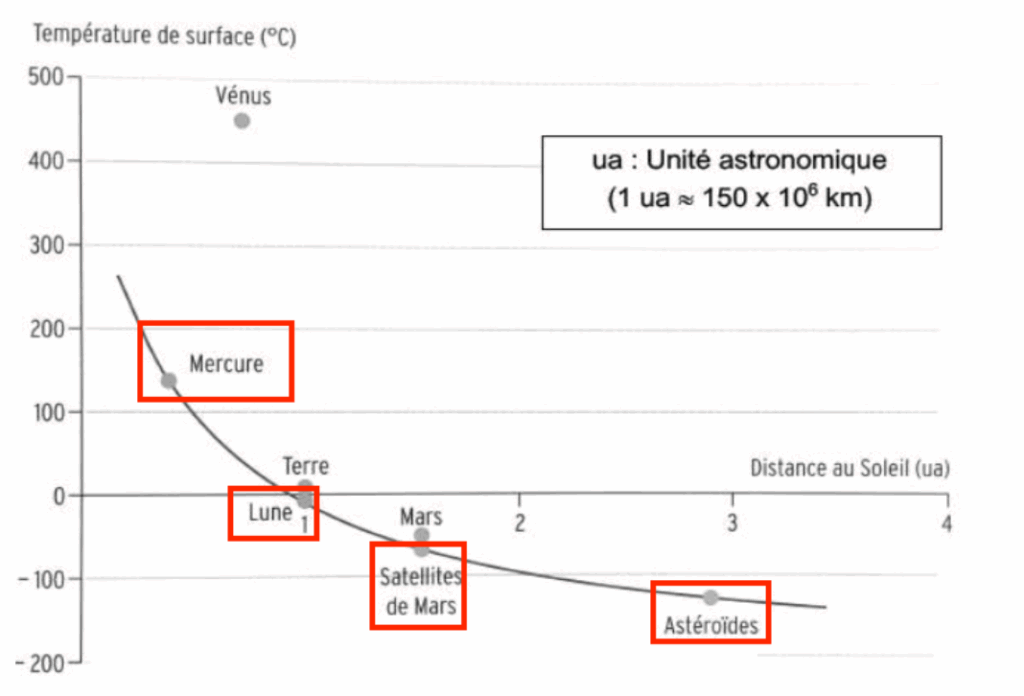
Ces objets ont en commun un albédo très faible 0,07.

5 – À partir de vos connaissances, expliquer qualitativement l’influence de l’albédo et de l’effet de serre sur la température terrestre moyenne.

L’albédo influence la température terrestre moyenne en déterminant la quantité de lumière solaire réfléchie par la surface de la Terre : un albédo élevé renvoie plus de lumière et réduit l’absorption de chaleur, abaissant ainsi la température.

L’effet de serre, en revanche, réchauffe la Terre en emprisonnant la chaleur dans l’atmosphère grâce aux gaz à effet de serre, augmentant la température moyenne.

6- Proposer une explication du fait que la température de Vénus est « anormalement » élevée par rapport aux autres objets considérés.

Vénus a un albédo élevé et un effet de serre atmosphérique très marqué. Ces deux paramètres contribuent à une augmentation de la température sur Vénus (voir question précédente).

C’est pourquoi la température de Vénus est « anormalement » élevée par rapport aux autres objets considérés.

Document réponse à rendre avec la copie

Annexe 1 – Partie 1 – Questions 1- et 2-b-

Annexe 2 – Partie 1 – Question 2-a-

𝑑 (en m)	0,2	0,3	0,4	0,5	0,6	0,8	1
𝑓(𝑑) (en lux)	10 800	4 800	⋯	1 728	⋯	675	⋯