Asie 2025 Sujet 2
Exercice 2 – (6 points) – Durée 1h03 – Calculatrice autorisée
Sujet n°25-PYCJ2JA1
Sujet et corrigé
Exercice 2 – Slam dunk au golf (6 points)
Au golf, un slam dunk est un coup qui consiste à envoyer la balle directement dans le trou sans qu’elle ne roule. Des conditions très spécifiques sont à rassembler pour que le golfeur puisse réaliser ce coup spectaculaire.
Dans la première partie de cet exercice, on s’intéresse à une méthode de mesure de la vitesse initiale d’une balle de golf. Puis, on identifie les conditions permettant de réaliser un slam dunk.
Partie 1 – Mesure de la vitesse initiale d’une balle de golf
Document – Radar de mesure
La valeur de la vitesse initiale d’une balle de golf peut être déterminée grâce à un radar
placé derrière le joueur.
L’appareil utilise un émetteur qui génère une onde électromagnétique de fréquence
$f_E = 21{,}125\ \text{GHz}$ ainsi qu’un récepteur qui capte l’onde après réflexion sur la balle.
La différence $\Delta f$ entre la valeur de la fréquence de l’onde émise et celle de l’onde reçue
permet d’accéder à la valeur de la vitesse $v$ de la balle qui s’affiche sur l’écran du radar
grâce à la relation : $|\Delta f|=\dfrac{2\times v}{c}\times f_E$.
Données :
- Célérité d’une onde électromagnétique dans le vide ou dans l’air : c = 3,00 × 108 m·s−1
- Intensité de la pesanteur : g = 9,81 m·s−2
- 1 GHz = 109 Hz
À la suite de la frappe réalisée par une golfeuse, un radar mesure un décalage de fréquence dont la valeur absolue est IΔf I = 4 225 Hz.
Q1- Nommer le phénomène physique lié au décalage de fréquence.
Le phénomène physique lié au décalage de fréquence est l’effet Doppler.
Q2- Calculer la valeur de la vitesse initiale v0 de la balle frappée par la joueuse.
$$\Delta f = 2\times \frac{v}{c}\times f_E$$
$$\Delta f = 2\times \frac{v_0}{c}\times f_E$$
$$\frac{2\times v_0}{c}\times f_E = \Delta f$$
$$v_0 = \frac{\Delta f\times c}{2\times f_E}$$
$$v_0 = \frac{4225\times 3,00\times 10^8}{2\times 21,125\times 10^9}$$
$$v_0 = 30,0\ \text{m.s}^{-1}$$
Partie 2 – Conditions de réalisation d’un slam dunk
On étudie le mouvement du centre de masse $G$ d’une balle de golf de masse $m$ dans le
référentiel terrestre supposé galiléen muni d’un repère $(O, \vec{i}, \vec{j})$.
À l’instant initial, le centre de masse $G$ est positionné à une hauteur $h$ du sol et à une
distance $d$ du trou. La balle est lancée dans le plan vertical repéré par les axes $(Ox, Oy)$
avec un vecteur vitesse $\vec{v_0}$ faisant un angle $\alpha$ avec l’axe $Ox$ (figure 1).
La balle évolue dans le champ de pesanteur terrestre $\vec{g}$. On néglige les forces de frottement
dues à l’air et la rotation de la balle.
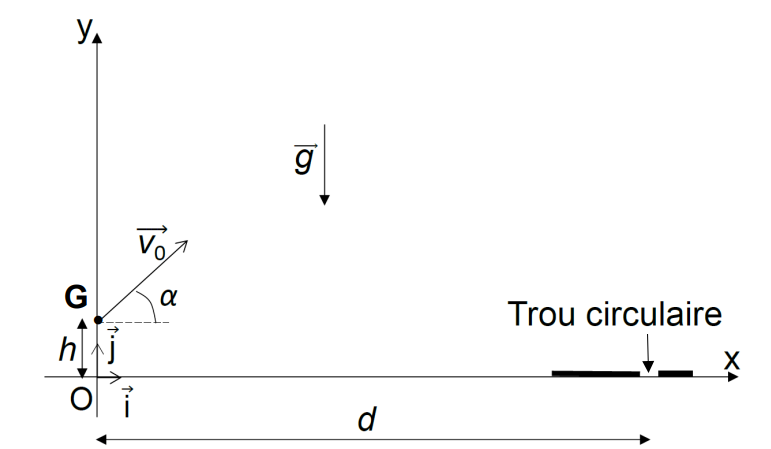
Figure 1 : Schéma du lancer de la balle de golf de centre de masse G à l’instant initial
Données :
- Masse de la balle de golf : m = 46 g
- Hauteur initiale du centre de masse : h = 3,0 cm
- Distance entre le centre de masse G de la balle et le trou : d = 1,5 x 102 m
Q3- Déterminer les expressions littérales des coordonnées ax et ay du vecteur accélération $\vec{a}$ du centre de masse G de la balle suivant les axes Ox et Oy.
Système {balle de golf}
Référentiel terrestre supposé galiléen
D’après la deuxième loi de newton :
$$\Sigma\overrightarrow{F_{ext}} = m\overrightarrow{a}$$
$$\overrightarrow{P} = m\overrightarrow{a}$$
$$m\overrightarrow{g} = m\overrightarrow{a}$$
$$\overrightarrow{g} = \overrightarrow{a}$$
$$\overrightarrow{g}\begin{pmatrix}0\\-g\end{pmatrix}$$
Le vecteur accélération du centre d’inertie du solide est égal au vecteur champ de pesanteur.
$$\overrightarrow{a}\begin{pmatrix}a_x(t)=0 \\ a_y(t)=-g\end{pmatrix}$$
Q4- Montrer que les équations horaires de son mouvement sont :
Montrer que les équations horaires de son mouvement sont :
$\overrightarrow{OG}(t)$
$x(t) = \left(v_0 \cos(\alpha)\right) t$
$y(t) = -\dfrac{1}{2} g t^2 + \left(v_0 \sin(\alpha)\right) t + h$
$$\overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}$$
$$\overrightarrow{v}\begin{pmatrix}v_x(t)=C_1\\v_y(t)=-gt+C_2\end{pmatrix}$$
$$\overrightarrow{v_0}\begin{pmatrix}v_{0x}=v_0\cos\alpha\\v_{0y}=v_0\sin\alpha\end{pmatrix}$$
$$\overrightarrow{v}\begin{pmatrix}v_x(t)=v_0\cos\alpha\\v_y(t)=-gt+v_0\sin\alpha\end{pmatrix}$$
$$\overrightarrow{v}=\frac{d\overrightarrow{OG}}{dt}$$
$$\overrightarrow{OG}\begin{pmatrix}x(t)=v_0\cos(\alpha)\times t + C_3\\y(t)=-\frac12 gt^2 + v_0\sin(\alpha)\times t + C_4\end{pmatrix}$$
$$\overrightarrow{OG_0}\begin{pmatrix}x_0=0\\y_0=h\end{pmatrix}$$
$$\overrightarrow{OG}\begin{pmatrix}x(t)=v_0\cos(\alpha)\times t\\y(t)=-\frac12 gt^2 + v_0\sin(\alpha)\times t + h\end{pmatrix}$$
Q5- En déduire que l’équation de la trajectoire du centre de masse de la balle dans le repère d’espace (Ox, Oy) s’écrit :
$$ y(x) = -\dfrac{1}{2} g \left( \dfrac{x}{v_0 \cos(\alpha)} \right)^2 + x \tan(\alpha) $$
Isolons $t$ :
$t=\frac{x}{v_0\cos(\alpha)}$
Remplaçons $t$ dans $y$ :
$$y(t)=-\frac12 gt^2+v_0\sin(\alpha)\times t + h$$
$$y(x)=-\frac12 g\left(\frac{x}{v_0\cos(\alpha)}\right)^2+v_0\sin(\alpha)\times\frac{x}{v_0\cos(\alpha)}+h$$
$$y(x)=-\frac12 g\times\left(\frac{x}{v_0\cos(\alpha)}\right)^2+x\times\tan(\alpha)+h$$
Q6- Indiquer les paramètres initiaux de lancement sur lesquels la joueuse peut intervenir pour réussir le slam dunk.
La trajectoire dépend des conditions initiales $(v_0, \alpha, h)$.
Ainsi, les paramètres initiaux de lancement sur lesquels la joueuse peut intervenir pour réussir le slam dunk sont :
- La vitesse initiale $v_0$
- L’angle $\alpha$
- La hauteur $h$
Une joueuse amateure frappe la balle avec un angle a = 39° et une vitesse initiale de valeur v0 = 30 m·s−1.
Q7- Indiquer si, dans ces conditions, la joueuse réussit un slam dunk.
Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et doit être correctement présentée.
D’après le sujet : « Au golf, un slam dunk est un coup qui consiste à envoyer la balle directement dans le trou sans qu’elle ne roule »
D’après le sujet : « Au golf, un slam dunk est un coup qui consiste à envoyer la balle directement dans le trou sans qu’elle ne roule »
Méthode 1 :
Calculons la portée du tir : xsol pour lequel la balle touche le sol y=0
$$0=-\frac{1}{2}\times 9,81\times \left(\frac{x}{30,0\times \cos{\left(39\right)}}\right)^2+x\times \tan{\left(39\right)}+3,0\times {10}^{-2}$$
$$0=-9,0\times {10}^{-3}\times x^2+0,81\times x +3,0\times{10}^{-2}$$
C’est une équation du second degré :
$$\Delta=b^2-4ac$$
$$\Delta=\left(0,81\right)^2-4\times-9,0\times {10}^{-3}\times 3,0\times {10}^{-2}$$
$$\Delta=0,66$$
$$x_{sol1}=\frac{-b+\sqrt\Delta}{2a}$$
$$x_{sol1}=\frac{-\left(0,81\right)+\sqrt{0,66}}{2\times -9,0\times {10}^{-3}}$$
$$x_{sol1}=-0,13\ m$$
Or x est positif
$$x_{sol2}=\frac{-b-\sqrt\Delta}{2a}$$
$$x_{sol2}=\frac{-\left(0,81\right)-\sqrt{0,66}}{2\times -9,0\times{10}^{-3}}$$
$$x_{sol2}=90\ m$$
On garde la valeur positive de xsol soit 90m.
D’après l’énoncé : « la distance entre le centre de masse G de la balle et le trou : d = 1,5 x 102 m »
Or la balle tombe à 90 m : la joueuse ne réussit pas un slam dunk.
Méthode 2 :
Calculons y pour x=d :
$$y\left(x=d\right)=-\frac{1}{2}g\times \left(\frac{d}{v_0\times \cos(\alpha)}\right)^2+d\times \tan{\left(\alpha\right)}+h$$
$$y\left(x=d\right)=-\frac{1}{2}\times 9,81\times \left(\frac{1,5\times {10}^2}{30,0\times \cos{\left(39\right)}}\right)^2+1,5\times {10}^2\times \tan{\left(39\right)}+3,0\times {10}^{-2}$$
$$y\left(x=d\right)=-82\ m$$
Pour x=d , l’altitude y n’est pas nulle.
Ainsi, la joueuse ne réussit pas un slam dunk.
