Utilisation médicale du technétium

Métropole 2025 Sujet 2 Bis

Exercice 3 – (6 points) –  Durée 1h03 – Calculatrice autorisée

Sujet n°25-PYCJ2ME4

Sujet et corrigé

Exercice 3 – Utilisation médicale du technétium (6 points)

Les noyaux de technétium 99 radioactifs, notés ⁹⁹Tc*, sont émetteurs de rayonnements gamma (g) utilisés dans les services de médecine nucléaire lors d’examens d’imagerie médicale tels que les scintigraphies osseuses. Produits dans le monde par uniquement dix réacteurs nucléaires, dont le réacteur Osiris du CEA en France, ces noyaux sont utilisés pour environ 500 000 examens médicaux par an en France. Dès 2014, le gouvernement français a lancé une alerte sur une pénurie durable à venir de noyaux de technétium 99, liée à la vétusté et l’arrêt programmé du fonctionnement de certains réacteurs nucléaires qui en assurent la production. Des mesures de gestion de cette pénurie ont été proposées par le Conseil National Professionnel de Médecine Nucléaire.

D’après Revue Médicale Suisse du 5 mars 2014 
https://www.sfen.org/rgn/fermeture-reacteur-osiris-risque-sante-publique

Les objectifs de cet exercice sont d’étudier la production et l’utilisation médicale du technétium, puis de discuter des pistes envisagées pour gérer la pénurie de cet isotope.

1.  Production de technétium

Les noyaux de technétium 99 s’obtiennent par désintégration de type β des noyaux de molybdène 99, notés ⁹⁹Mo.

Les services de médecine nucléaire reçoivent des mélanges de noyaux molybdène 99 / technétium 99, ils bénéficient ainsi d’une source en technétium 99 pour quelques jours seulement.

Données :

• extrait du diagramme (N,Z) des éléments de numéros atomiques Z = 42 et Z = 43 :

• temps de demi-vie :

Noyau de molybdène 99	Noyau de technétium 99
66 h pour la désintégration de type β	6 h pour l’émission de rayonnement gamma (γ)

Q1. Donner la composition du noyau de molybdène 99.

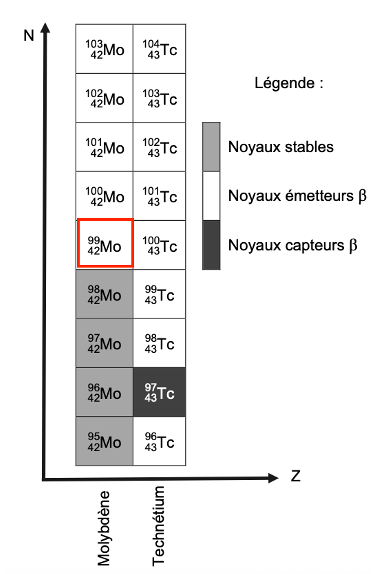
Q2. Rappeler la définition des termes « noyaux isotopes ». En déduire, à l’aide du diagramme (N,Z), deux isotopes stables du molybdène 99.

Q3. Écrire l’équation de la désintégration des noyaux de molybdène 99 en noyaux de technétium 99. Donner le nom de la particule émise lors de cette désintégration.

Équation de la désintégration des noyaux de molybdène 99 en noyaux de technétium 99 :
${_{42}^{99}}Mo\longrightarrow{_{43}^{99}}Tc+{_Z^A}X$

Pour trouver A et Z on utilise les lois de Soddy :
Conservation du nombre de nucléons :
$99=99+A$
$99+A=99$
$A=99-99$
$A=0$

Conservation du nombre de charge :
$42=43+Z$
$43+Z=42$
$Z=42-43$
$Z=-1$

Ainsi ${_Z^A}X={_{-1}^0}e$

Ainsi, la particule émise lors de cette désintégration est un électron.

Q4. Après avoir rappelé la définition du temps de demi-vie, justifier que les services de médecine nucléaire bénéficient d’une source de technétium 99 pour quelques jours seulement.

Le temps de demi-vie $t_{1/2}$ est la durée au bout de laquelle le nombre de noyau radioactif (ou l’activité) a été divisée par 2.
Au bout de 7 demi-vies, il reste moins de 1% des noyaux radioactifs initialement présents.
$7\ \times\ t_{1/2}=7\ \times\ 6=42h$
$\frac{42}{24}=1,75\ jour\ =\ 1\ jour\ et\ 18h$
Ainsi, les services de médecine nucléaire bénéficient d’une source de technétium 99 pour quelques jours seulement.

2.  Utilisation médicale de technétium en scintigraphie

Lors d’une scintigraphie, on injecte au patient une solution contenant une molécule marquée au technétium ⁹⁹Tc* qui se fixe sur les os en moins de deux heures. Après l’injection de la solution, le patient attend donc deux à trois heures avant que les clichés soient réalisés à l’aide d’une caméra sensible aux rayons gamma, appelée gamma-caméra.

Données :

• constante de Planck : h = 6,63×10^–34 J·s ;
• 1 eV = 1,60×10^–19 J ;
• énergie E d’un photon associé à un rayonnement de fréquence n : E = h·ν ;
• gamme de fréquences n des différents types de rayonnements électromagnétiques :

• le technétium ⁹⁹Tc* émet principalement des photons d’énergie : E_Tc = 141 keV ;
• le technétium ⁹⁹Tc* a une demi-vie de 6 h ;l’activité de la quantité injectée de technétium ⁹⁹Tc* au patient à la date t = 0, notée A₀, est de l’ordre de 700 MBq pour un patient dont la masse est 80 kg;
• on rappelle l’équation différentielle vérifiée par le nombre de noyaux radioactifs N(t) d’un échantillon à l’instant t :

$$\frac{dN(t)}{dt} + \lambda N(t) = 0$$

λ étant la constante radioactive du technétium ⁹⁹Tc* ;

• l’activité d’une source radioactive, A(t), s’exprime en becquerel (Bq) et a pour expression :

A(t) = λ·N(t)

Q5. Vérifier que l’énergie des photons émis par le ⁹⁹Tc* est compatible avec l’utilisation d’une gamma-caméra pour réaliser les clichés lors d’une scintigraphie.

D’après les données :
$E=h\times \nu$
$h\times \nu=E$
$\nu=\frac{E}{h}$
$\nu=\frac{141\times {10}^3\times 1,6\times {10}^{-19}}{6,63\times {10}^{-34}}$
$\nu=3,4\times {10}^{19}\ Hz$

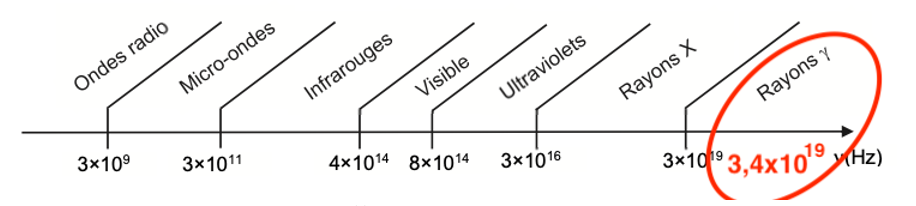
L’énergie des photons émis par le ⁹⁹Tc correspond aux rayons gamma.

Ainsi, l’énergie des photons émis par le ⁹⁹Tc est compatible avec l’utilisation d’une gamma-caméra pour réaliser les clichés lors d’une scintigraphie.

Q6. Justifier l’utilisation d’un protège-seringue possédant un blindage à base de verre au plomb pour la réalisation de l’injection de la solution au patient.

Le plomb ne laisse pas passer les rayons gamma.

Pour la réalisation de l’injection de la solution au patient, afin de protéger les manipulateurs de la seringue des rayons gamma, on utilise un protège-seringue possédant un blindage à base de verre au plomb.

Q7. Résoudre l’équation différentielle afin d’exprimer le nombre de noyaux radioactifs de technétium ⁹⁹Tc* à l’instant t, noté N(t), en fonction du nombre initial de noyaux radioactifs à l’instant t = 0, noté N₀, et de la constante radioactive λ.

$\frac{dN\left(t\right)}{dt}+\lambda\times N\left(t\right)=0$
Solution de l’équation différentielle :
$N\left(t\right)=N_0\times e^{-\lambda t}$

Dérivons $N\left(t\right)$ :
$\frac{dN\left(t\right)}{dt}=N_0\times -\lambda\times e^{-\lambda t}$
$\frac{dN\left(t\right)}{dt}=-\lambda\times N_0\times e^{-\lambda t}$
$\frac{dN\left(t\right)}{dt}=-\lambda\times N\left(t\right)$
On retrouve l’équation différentielle :
$\frac{dN\left(t\right)}{dt}+\lambda\times N\left(t\right)=0$

Ainsi, $N\left(t\right)=N_0\times e^{-\lambda t}$ est solution de l’équation différentielle.

Q8. Montrer que l’expression de l’activité A(t) du technétium ⁹⁹Tc* en fonction de l’activité initiale A0 injectée au patient et de la constante radioactive λ s’écrit A(t) = A ⋅e^–λ⋅t .

$A\left(t\right)=\lambda\times N\left(t\right)$
Or
$N\left(t\right)=N_0\times e^{-\lambda t}$
D’où
$A\left(t\right)=\lambda\times N_0\times e^{-\lambda t}$
Or
$A_0=\lambda\times N_0$
D’où
$A\left(t\right)=\lambda\times N_0\times e^{-\lambda t}$
$A\left(t\right)=A_0\times e^{-\lambda t}$

Q9. Montrer que la constante radioactive λ et le temps de demi-vie t1/2 sont reliés par la relation :

$t_{1/2}$ est la durée au bout de laquelle l’activité de noyau radioactif a été divisée par 2.
$A(t_{1/2})=\frac{A_0}{2}$

Or
$A(t_{1/2})=A_0\times e^{-\lambda t_{1/2}}$

Ainsi
$A_0\times e^{-\lambda t_{1/2}}=\frac{A_0}{2}$
$e^{-\lambda t_{1/2}}=\frac{1}{2}$
$ln\left(e^{-\lambda t_{1/2}}\right)=ln\left(\frac{1}{2}\right)$
$-\lambda t_{1/2}=-ln\left(2\right)$
$\lambda=\frac{ln\ 2}{t_{1/2}}$

Tant que l’activité du technétium ⁹⁹Tc* dans le corps du patient est supérieure à 3 % de l’activité initiale injectée, des mesures de précaution doivent être respectées par le patient (rester éloigné des femmes enceintes et des jeunes enfants, nettoyer soigneusement les toilettes après chaque utilisation, etc.).

Q10. Déterminer la durée pendant laquelle le patient doit respecter ces précautions en supposant que la diminution de l’activité du technétium ⁹⁹Tc* dans le corps du patient n’est due qu’à la décroissance radioactive.

D’après l’énoncé : Tant que l’activité du technétium 99Tc dans le corps du patient est supérieure à 3 % de l’activité initiale injectée, des mesures de précaution doivent être respectées par le patient.
Soit
$A\left(t\right)=\frac{3}{100}\times A\left(0\right)$

Trouvons le temps correspondant :
$A\left(t\right)=A\left(0\right)\times e^{-\lambda\times t}$
$A\left(0\right)\times e^{-\lambda\times t}=A\left(t\right)$
$e^{-\lambda\times t}=\frac{A\left(t\right)}{A\left(0\right)}$
$ln\left(e^{-\lambda\times t}\right)=ln\left(\frac{A\left(t\right)}{A\left(0\right)}\right)$
$-\lambda\times t=ln\left(\frac{A\left(t\right)}{A\left(0\right)}\right)$
$t=\frac{ln\left(\frac{A\left(t\right)}{A\left(0\right)}\right)}{-\lambda}$
$t=-\frac{ln\left(\frac{A\left(t\right)}{A\left(0\right)}\right)}{\lambda}$
Or
$\lambda=\frac{ln\ 2}{t_{1/2}}$

$t=-\frac{ln\left(\frac{A\left(t\right)}{A\left(0\right)}\right)}{\frac{ln\ 2}{t_{1/2}}}$
$t=-ln\left(\frac{A\left(t\right)}{A\left(0\right)}\right)\times \frac{t_{1/2}}{ln\ 2}$
Or
$A\left(t\right)=\frac{3}{100}\times A\left(0\right)$

$t=-ln\left(\frac{\frac{3}{100}\times A\left(0\right)}{A\left(0\right)}\right)\times \frac{t_{1/2}}{ln\ 2}$
$t=-ln\left(\frac{3}{100}\right)\times \frac{t_{1/2}}{ln\ 2}$
$t=-ln\left(\frac{3}{100}\right)\times \frac{6}{ln\ 2}$
$t=30\ h$

Ainsi, en supposant que la diminution de l’activité du technétium 99Tc dans le corps du patient n’est due qu’à la décroissance radioactive, la durée pendant laquelle le patient doit respecter ces précautions est de 30h.

3.  Pistes pratiques pour gérer les périodes de pénurie de technétium 99

Le technétium ⁹⁹Tc* est obtenu par désintégration du molybdène 99 (⁹⁹Mo) issu de réactions de fission dans les réacteurs nucléaires. La fermeture progressive de certains réacteurs nucléaires entraine une diminution de la production mondiale en molybdène 99.

Pour les scintigraphies cardiaques, il est possible d’utiliser des traceurs marqués au thallium 201 (²⁰¹Tℓ*) à la place du technétium 99 (⁹⁹Tc*).

Donnée :

• tableau comparatif des principales caractéristiques de deux radioéléments :

Noyau	Thallium 201	Technétium 99
Symbole	201Tℓ*	99Tc*
Temps de demi-vie	3,04 jours pour le rayonnement γ d’énergie 167 keV	6 h pour le rayonnement γ d’énergie 141 keV
Coût d’un examen cardiaque	0,8267 €/MBq	0,0378 €/MBq
Nombre d’injections lors de l’examen	1	2

Q11. Identifier, en justifiant, un avantage et un inconvénient au remplacement du technétium 99 (⁹⁹Tc*) par du thallium 201 (²⁰¹Tℓ*).

Avantage au remplacement du technétium 99 (⁹⁹Tc*) par du thallium 201 (²⁰¹Tℓ*) :

Le thallium 201 (²⁰¹Tℓ*) nécessite 1 injection contre 2 pour le technétium 99 (⁹⁹Tc*). C’est plus simple et ça n’nécessite moins de manipulations.

Inconvénient au remplacement du technétium 99 (⁹⁹Tc*) par du thallium 201 (²⁰¹Tℓ*) :

Le temps de demi-vie du thallium 201 (²⁰¹Tℓ*) beaucoup plus long 3,04 jours contre 6 h pour le technétium 99 (⁹⁹Tc*) : le patient reste radioactif bien plus longtemps.

Le coût d’un examen cardiaque est activité supérieure : 0,8267 €/MBq pour thallium 201 (²⁰¹Tℓ*) contre 0,0378 €/MBq pour le technétium 99 (⁹⁹Tc*).