Le réfrigérateur

Métropole Septembre 2025 Sujet 2

Exercice 3 – (6 points) –  Durée 1h03 – Calculatrice autorisée

Sujet n°25-PYCJ2ME3

Élément indispensable des cuisines et des magasins, le réfrigérateur n’a cessé d’être perfectionné depuis le premier brevet déposé en 1835 par Jacob Perkins. Il nous permet d’avoir à portée de main un endroit frais.

Les objectifs de cet exercice sont :

  • d’étudier dans une première partie le refroidissement d’une bouteille d’eau placée dans un réfrigérateur « A » destiné à maintenir au frais des boissons à la température d’environ 7 °C ;
  • d’étudier dans une seconde partie la difficulté d’ouverture d’une porte d’un réfrigérateur « B » dans deux situations différentes.
1.  La température « idéale » d’une bouteille d’eau pour optimiser l’hydratation

Données :

  • le système étudié dans cette partie est une bouteille d’eau notée S ;
  • volume du système S : VS = 1,5 L ;
  • masse volumique du système S : ρS = 1,00 kg·L–1 ;
  • capacité thermique massique du système S : cS = 4,18×103 J·K–1·kg–1 ;
  • la température idéale de consommation de l’eau, afin d’optimiser la réhydratation du corps humain, est : θdéale = 16 °C ;
  • la loi de Newton donne l’expression du flux thermique Φ (en W) reçu par le système S, à une température θ(t), de la part de l’air intérieur du réfrigérateur dont la température θréfri est considérée constante :

Φ = α·(θréfri – θ(t))

où α = 0,50 W·K–1 est une estimation du coefficient d’échange thermique entre le système S et l’air intérieur du réfrigérateur.

À l’instant t = 0, on place le système S dans le réfrigérateur « A », on ferme la porte de ce réfrigérateur puis on mesure la température θ(t) du système S à intervalle de temps régulier pendant une demi-journée.

Q1. Caractériser qualitativement le phénomène de convection, un des modes de transfert thermique ayant lieu entre S et son environnement.

Q2. Indiquer, en justifiant, le sens du transfert thermique Q dans le cas étudié. L’utilisation d’un tableur-grapheur permet d’obtenir :

  • le tracé de la courbe de température expérimentale à partir des mesures effectuées ;
  • le tracé d’une courbe de modélisation de l’évolution temporelle de la température θ(t) du système S à l’aide d’une fonction de la forme générale :

$\theta(t) = A\cdot e^{-t/\tau} + B$ où A, B et t sont des constantes.

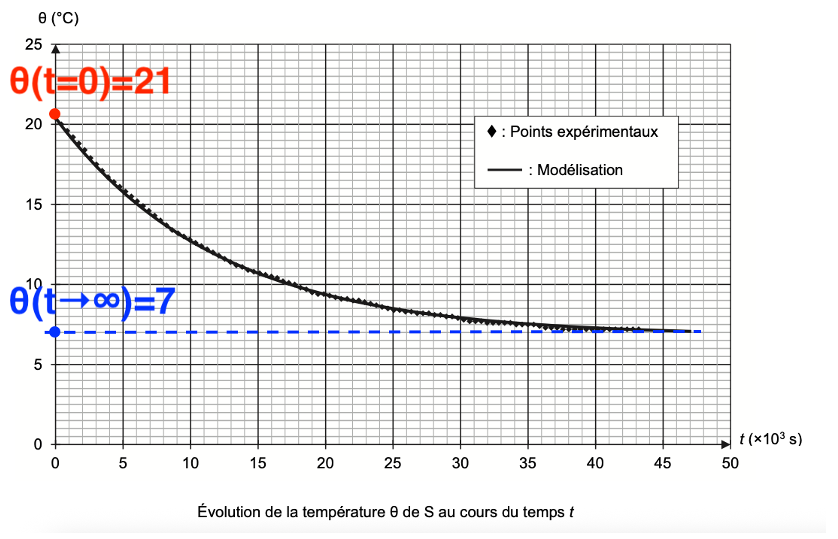
Ces deux courbes sont représentées sur la figure 1 de l’ANNEXE À RENDRE AVEC LA COPIE.

Q3. Exprimer θ(t = 0) puis la limite de θ(t) quand $t \to +\infty$ en fonction des constantes A et B. En déduire, en utilisant la figure 1 de l’ANNEXE À RENDRE AVEC LA COPIE, des valeurs des constantes A et B en précisant leur unité respective.

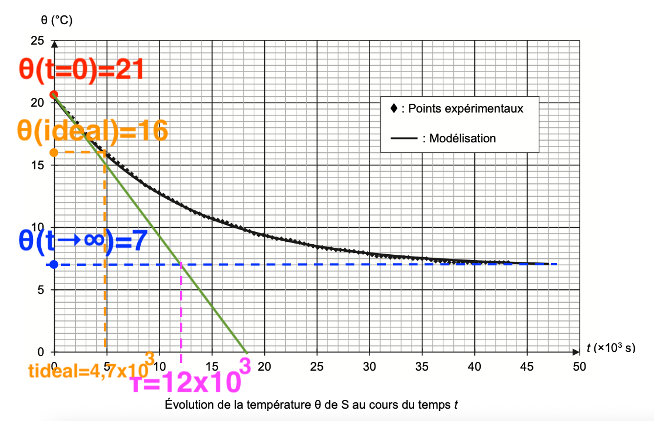
Q4. Montrer graphiquement, en faisant apparaître la construction sur la figure 1 de l’ANNEXE À RENDRE AVEC LA COPIE, que la valeur de la constante t est de l’ordre de 12×103 s.

On cherche à déterminer par un modèle l’équation différentielle vérifiée par la fonction θ(t). Pour cela, on effectue un bilan d’énergie pour le système S, entre les instants t et t + Δt.

Q5. Appliquer le premier principe de la thermodynamique au système S entre t et t + Δt pour exprimer la variation de température θ(t + Δt) – θ(t) en fonction de Δt, ρS, VS, cS, α et (θréfri – θ(t)).

On en déduit que l’équation différentielle régissant l’évolution de la température θ(t) s’écrit :

$$\frac{d\theta(t)}{dt} + \frac{1}{\tau}\theta(t) = \frac{\theta_{\text{réfri}}}{\tau}$$

avec $$\tau = \frac{\rho_S\cdot V_S\cdot c_S}{\alpha}.$$

La solution de cette équation différentielle a pour expression :

$$\theta(t) = (\theta_0 – \theta_{\text{réfri}})\cdot e^{-t/\tau} + \theta_{\text{réfri}}$$

On donne pour l’expérience réalisée : θ0 = 20,4 °C et θréfri = 6,8 °C.

Q6. Établir, selon cette modélisation, en fonction de t , θ0, θréfri et θidéale, l’expression de la durée tidéale nécessaire pour que le système S atteigne la température idéale de consommation d’une boisson.

Q7. Calculer cette durée tidéale, sachant que θidéale = 16 °C. Indiquer si cette durée est cohérente avec le graphique de l’ANNEXE À RENDRE AVEC LA COPIE. Une construction graphique est attendue.

2.  Ouverture de la porte du réfrigérateur « B »

Dans des conditions d’usage régulier, l’ouverture de la porte d’un autre réfrigérateur nommé « B » est parfois difficile. Un élément d’explication de cette difficulté peut être envisagé en considérant la différence de pression entre l’air intérieur du réfrigérateur et l’air extérieur à celui-ci.

Mise en service du réfrigérateur

On étudie l’influence du changement de température lors de la mise en service du réfrigérateur sur la différence de pression.

Données :

  • l’air est considéré comme un gaz parfait ;
  • constante des gaz parfaits : R = 8,314 J·K–1·mol–1 ;
  • équation d’état du gaz parfait :

P·V = n·R·T

avec P la pression du gaz en Pa, V le volume occupé par le gaz en m3, n la quantité de matière de gaz en mol et T la température du gaz en K ;

  • volume d’air dans le réfrigérateur : Vréfri = 0,15 m3 ;
  • température de l’air ambiant extérieur au réfrigérateur : Tamb = 293 K ;
  • pression de l’air ambiant extérieur au réfrigérateur : Pamb = 1009,1×102 Pa ;
  • intensité de la pesanteur : g = 9,8 N·kg–1.

À la date t = 0, la porte du réfrigérateur, contenant de l’air à la température T0 = Tamb et à la pression P0 = Pamb, est fermée puis le réfrigérateur est mis en fonctionnement. On note T et P, respectivement la température et la pression de l’air intérieur du réfrigérateur à une date quelconque.

On fait l’hypothèse que le réfrigérateur constitue un système fermé, lorsque la porte est fermée : il n’échange pas de matière avec l’extérieur.

Q8. Expliquer pourquoi, dans le cadre de cette hypothèse, le quotient $\dfrac{P}{T}$ peut être considéré constant lors du refroidissement de l’air du réfrigérateur après la fermeture de la porte.

Q9. Calculer, dans ce modèle, la valeur, notée Pfinale, de la pression de l’air à l’intérieur du réfrigérateur lorsque la température intérieure a atteint sa valeur stabilisée égale à 277 K.

En réalité, on mesure à cette température une pression intérieure finale voisine de 1009,1×102 Pa.

Q10. Indiquer une raison possible de l’écart entre le résultat du calcul effectué à la question Q8 et la pression réellement mesurée.

Difficulté d’ouverture d’une porte de réfrigérateur juste après sa fermeture

Dans certains cas, la réouverture d’une porte de réfrigérateur juste après fermeture, peut s’avérer difficile. Afin d’expliquer ce phénomène, on enregistre la pression de l’air à l’intérieur du réfrigérateur lors d’une expérience pour laquelle, le réfrigérateur étant ouvert, on en ferme la porte à un instant t1. L’évolution de la pression mesurée est représentée sur la figure 2. On s’intéresse à la réouverture la porte après une durée Δt suivant la fermeture.

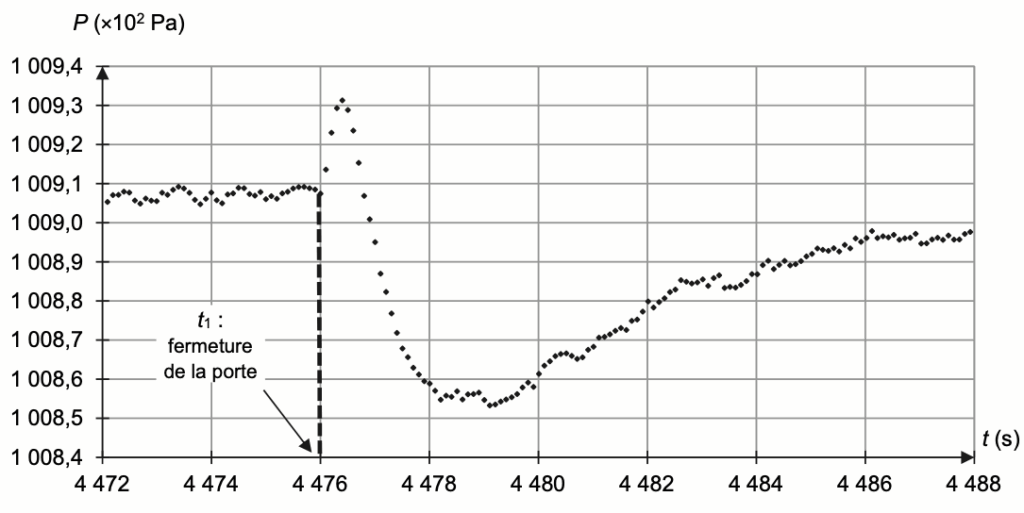
Figure 2. Évolution temporelle de la pression P de l’air intérieur du réfrigérateur S, avant et après fermeture de sa porte

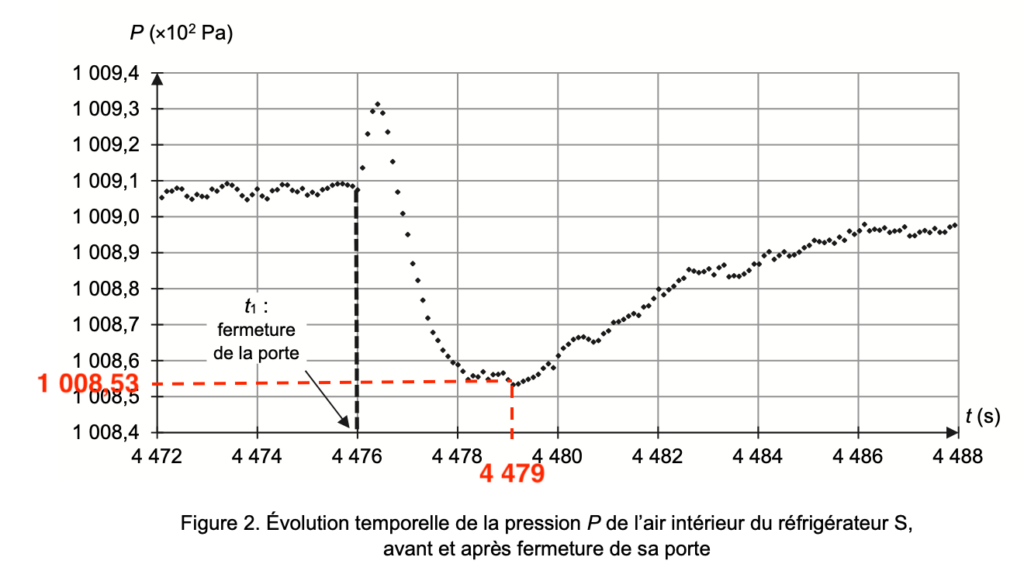
Q11. À l’aide de la figure 2, justifier qu’il peut être difficile de rouvrir la porte du réfrigérateur après une durée Δt = 3 s.

Q12. En assimilant la porte du réfrigérateur à une plaque rectangulaire solide très fine de surface Splaque = 1,2 m2, déterminer la valeur et la direction de la résultante $\vec{F}$ des forces pressantes qui s’appliquent sur cette plaque lorsque l’on souhaite rouvrir la porte après une durée $\Delta t = 3\ \text{s}$. Commenter le résultat obtenu.

ANNEXE À RENDRE AVEC LA COPIE

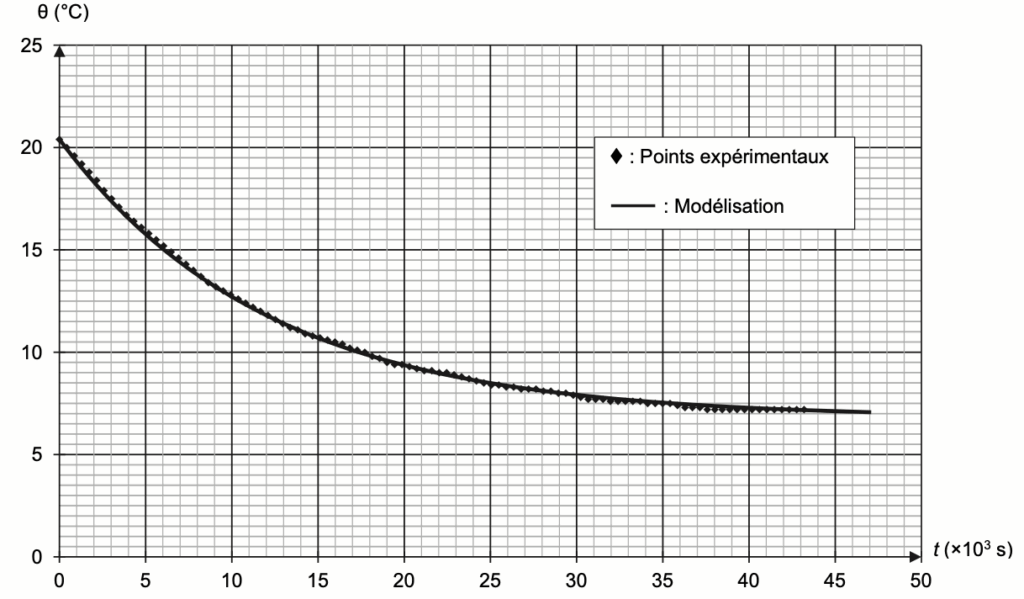
Évolution de la température θ de S au cours du temps t