Bac Amérique du sud 2025 Sujet 1
Exercice 1 – (11 points) – Durée 1h56 – Calculatrice autorisée
Sujet n°25-PYCJ1AS1
Sujet et corrigé
EXERCICE 1. Tour Montparnasse (11 points)
Du haut de ses 210 m et 59 étages, la tour Montparnasse est le plus grand gratte-ciel de la ville de Paris. Elle fera peau neuve d’ici peu : jardins, façades végétalisées, panneaux photovoltaïques, nouveau vitrage transparent et isolant. La future tour devrait à la fois changer d’aspect et améliorer ses performances énergétiques.
Cet exercice propose d’étudier, dans un premier temps, le mouvement d’un des ascenseurs équipant la tour. Il portera ensuite sur deux des mesures visant à améliorer les performances énergétiques du bâtiment.

1. Mouvement du grand ascenseur
L’objectif de cette première partie est d’étudier le mouvement du plus grand ascenseur de la tour, qui relie le rez-de-chaussée, pris comme référence d’altitude, au 56e étage. On étudie le mouvement, dans le référentiel terrestre supposé galiléen, du centre d’inertie de l’ascenseur dans le champ de pesanteur considéré comme uniforme. Le point O confondu avec le centre de masse de l’ascenseur lorsqu’il se situe au rez-de-chaussée sera pris comme origine d’un axe Oz orienté positivement vers le haut.
Données :
- loi fondamentale de la statique des fluides :
$$P_B – P_A = \rho \times g \times (z_A – z_B)$$
avec : 𝑃A, 𝑃B : pression du fluide en deux points A et B (en Pa) ;
𝜌 : masse volumique du fluide (en kg∙m−3) ;
𝑔 ∶ intensité de la pesanteur (en m∙s−2) ;
𝑧A, 𝑧B : altitude des points A et B (en m) ; - intensité de la pesanteur terrestre : $g = 9,81\ \text{m.s}^{-2}$ ;
- masse molaire de l’air dans les conditions de l’expérience : $M = 28,98\ \text{g.mol}^{-1}$ ;
- constante des gaz parfaits : $R = 8,314\ \text{J.mol}^{-1}\text{.K}^{-1}$ ;
- relation entre la température exprimée en kelvin et la température exprimée en degré Celsius :
$$T(K) = \theta(°C) + 273,15.$$
On se propose, dans un premier temps, de vérifier la hauteur parcourue par l’ascenseur lors d’un trajet, à partir d’un suivi de la pression atmosphérique réalisé grâce à un smartphone. On considère que l’air suit le modèle du gaz parfait. Les mesures obtenues permettent de tracer la courbe suivante.
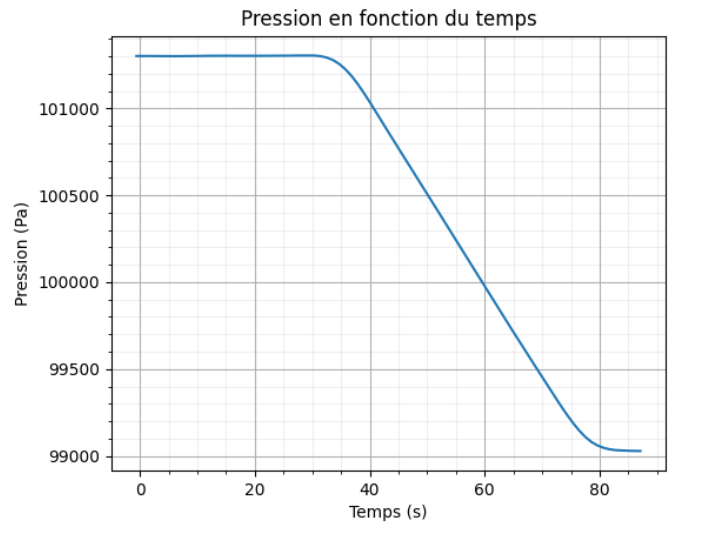
Figure 1. Courbe représentant l’évolution de la pression au cours d’un voyage dans le grand ascenseur Source : mesures réalisées par l’auteur de l’exercice
Q1. À l’aide de la figure 1, justifier qualitativement que l’ascenseur monte lors de l’expérience.
$P_B-P_A=\rho\times g\times \left(z_A-z_B\right)$
Lors d’une montée, ZB est supérieur à ZA.
$z_A<z_B$
$z_A-z_B<0$
$\rho\times g\times \left(z_A-z_B\right)<0$
$P_B-P_A=\rho\times g\times \left(z_A-z_B\right)<0$
D’ou
$P_B-P_A<0$
$P_B<P_A$
Ainsi, lors d’une montée, PB est inférieur à PA.
On remarque sur la figure 1 que PB est inférieur à PA. Ainsi, l’ascenseur monte lors de l’expérience.
Q2. Exprimer l’équation d’état d’un gaz parfait, en précisant la signification et les unités des différentes grandeurs.
L’équation d’état d’un gaz parfait s’écrit :
$P\times V=n\times R\times T$
Avec :
(P) est la pression du gaz en pascal (Pa)
(V) est le volume occupé par le gaz en mètre cube (m³)
(n) est la quantité de matière du gaz en mole (mol)
(R) est la constante des gaz parfaits : $R=8,314\ \ \mathrm{J.mo}\mathrm{l}^{\mathrm{-1}}\mathrm{.}\mathrm{K}^{\mathrm{-1}}$
(T) est la température du gaz en kelvin (K)
Le jour de l’expérience, la température était égale à 25,0 °C.
Q3. À l’aide de la question précédente, montrer que la valeur de la masse volumique de l’air au pied de la tour le jour de l’expérience est 𝜌𝑎𝑖𝑟 = 1,184 kg∙m−3.
$\rho_{air}=\frac{m_{air}}{V_{air}}$
Or
$n_{air}=\frac{m_{air}}{M_{air}}$
$\frac{m_{air}}{M_{air}}=n_{air}$
$m_{air}=n_{air} \times M_{air}$
D’où
$\rho_{air}=\frac{n_{air} \times M_{air}}{V_{air}}$
Or
$P \times V_{air}=n_{air} \times R \times T$
$n_{air} \times R \times T=P \times V_{air}$
$n_{air}=\frac{P \times V_{air}}{R \times T}$
D’où
$\rho_{air}=\frac{\frac{P \times V_{air}}{R \times T} \times M_{air}}{V_{air}}$
$\rho_{air}=\frac{P \times V_{air} \times M_{air}}{V_{air} \times R \times T}$
$\rho_{air}=\frac{P \times M_{air}}{R \times T}$
Or
$T=\theta+273,15$
D’où
$\rho_{air}=\frac{P \times M_{air}}{R \times \left(\theta+273,15\right)}$
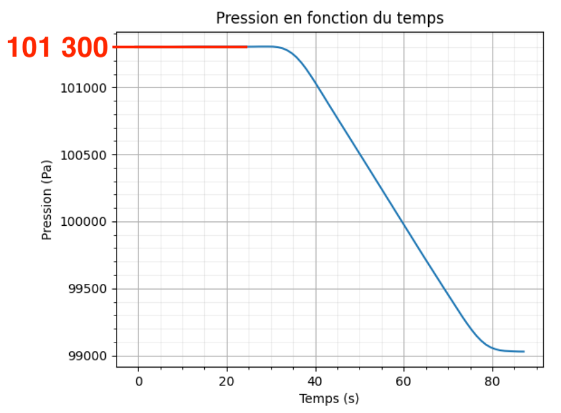
Graphiquement, au pied de la tour (à $t=0s$, avant la monté de l’ascenseur) le jour de l’expérience : $P=101\ 300\ Pa$
$\rho_{air}=\frac{101\ 300 \times 28,98}{8,314 \times \left(25,0+273,15\right)}$
$\rho_{air}=1184\ g.m^{-3}$
$\rho_{air}=1,184\ \ kg.m^{-3}$
Q4. Montrer que la hauteur ℎ atteinte par l’ascenseur à la fin de son trajet est telle que :
$$h = \dfrac{P_1 – P_2}{\rho_{air} \times g}$$
avec 𝑃1 et 𝑃2 les pressions respectivement au pied et au sommet de la tour.
$P_B-P_A=\rho \times g \times \left(z_A-z_B\right)$
$P_1-P_2=\rho_{air} \times g \times \left(z_2-z_1\right)$
Or
$z_2-z_1=h$
D’où
$P_1-P_2=\rho_{air} \times g \times h$
$\rho_{air} \times g \times h=P_1-P_2$
$h=\frac{P_1-P_2}{\rho_{air} \times g}$
Q5. Calculer la hauteur ℎ atteinte par l’ascenseur à la fin du trajet. Commenter.
$h=\frac{P_1-P_2}{\rho_{air} \times g}$
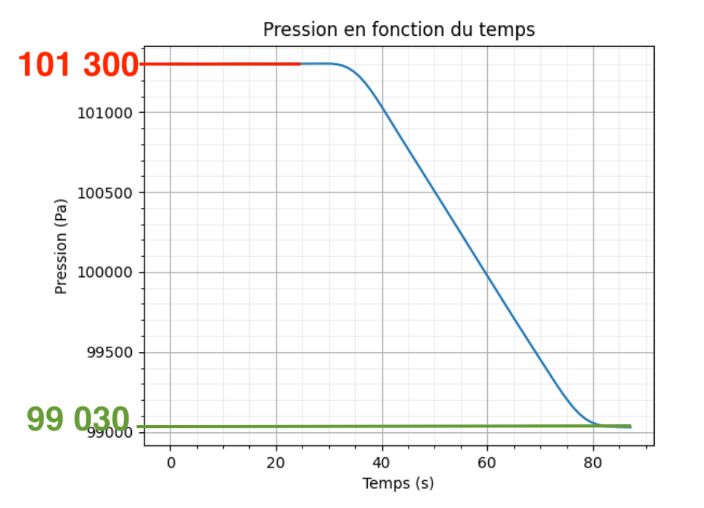
$h=\frac{101\ 300-99\ 030}{1,184 \times 9,81}$
$h=195\ m$
D’après l’énoncé : La tour Montparnasse est haut de 210 m.
Cette montée en ascenseur s’est faite jusqu’au sommet de la tour.
En plus de l’altitude finale de l’ascenseur, il peut être utile de connaître son altitude au cours du trajet. Cette donnée permet effectivement d’accéder à la vitesse de l’appareil, puis à son accélération. Les différentes opérations utiles sont réalisées ici à l’aide du programme en langage Python qui suit. Il contient, aux lignes 3 et 4, les 86 couples de valeurs (temps ; pression atmosphérique) enregistrés par le smartphone lors de la montée.
1 import matplotlib.pyplot as plt
2 #données expérimentales
3 t=[-0.58, 0.43, —, 86.01, 87.08] # valeurs du temps
4 p=[101302.07, 101302.09, —, 99028.37, 99028.04] # valeurs de pression
5
6 #initialisation des variables
7 z,v,a=[],[],[] #initialisation des listes z,v,a
8 rhoair,g=1.184,9.81 #masse volumique de l’air, intensité de la pesanteur
9 #calculs des valeurs de z, v et a
10 for i in range (len(t)-1): # calcul de l’altitude
11 zcalcul=(p[0]-p[i+1])/(rhoair*g)
12 z.append(zcalcul)
13
14 for i in range (len(z)-1): # calcul de la vitesse
15 vcalcul=(z[i+1]-z[i])/(t[i+1]-t[i])
16 v.append(vcalcul)
17
18 for i in range (len(v)-1): # calcul de l’accélération
19 acalcul=( )
20 a.append(acalcul)
Q6. Recopier puis compléter la ligne 19 du script Python ci-dessus pour calculer les valeurs de l’accélération.
L’accélération est définie par :
$a=\frac{v_{i+1}-v_i}{t_{i+1}-t_i}$
19 acalcul=(v[i+1] -v[i])/(t[i+1] -t[i])
Q7. Indiquer, en justifiant, le nombre de valeurs de l’accélération calculées par le programme.
Le programme compte 4 valeurs du temps.
Les altitudes z sont calculées dans une boucle allant de i = 0 à i = len(t)-1 donc 3 valeurs.
Les vitesses v sont calculées dans une boucle allant de i = 0 à i = len(z)-1 donc 2 valeurs.
les accélérations a sont calculées dans une boucle allant de i = 0 à i = len(v)-1 donc 1 valeur
La suite du programme permet de tracer les courbes des figures 2 et 3, représentant l’évolution de la vitesse et de l’accélération de l’ascenseur au cours du trajet étudié.
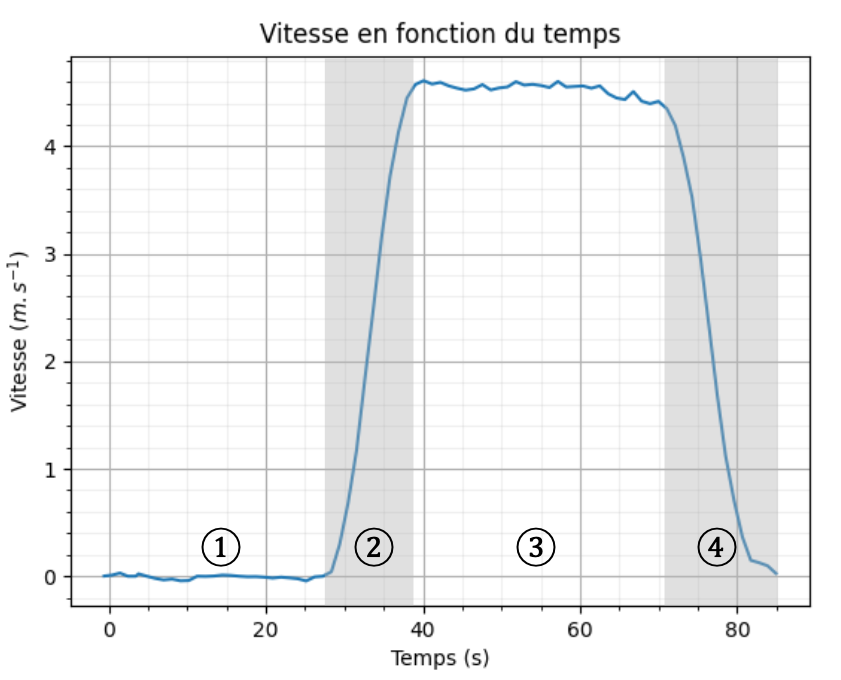
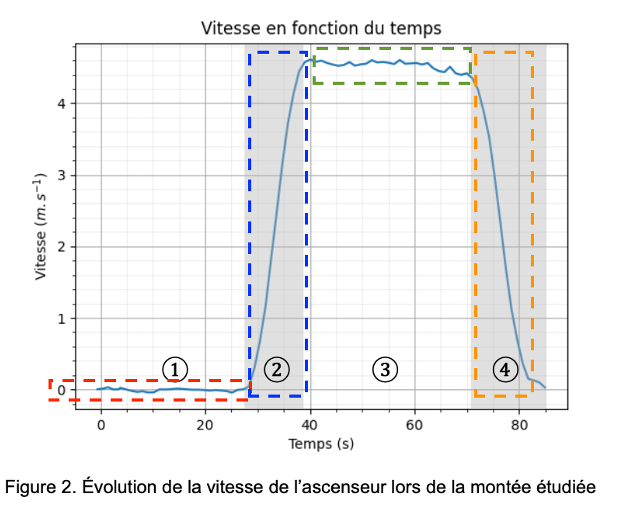
Figure 2. Évolution de la vitesse de l’ascenseur lors de la montée étudiée
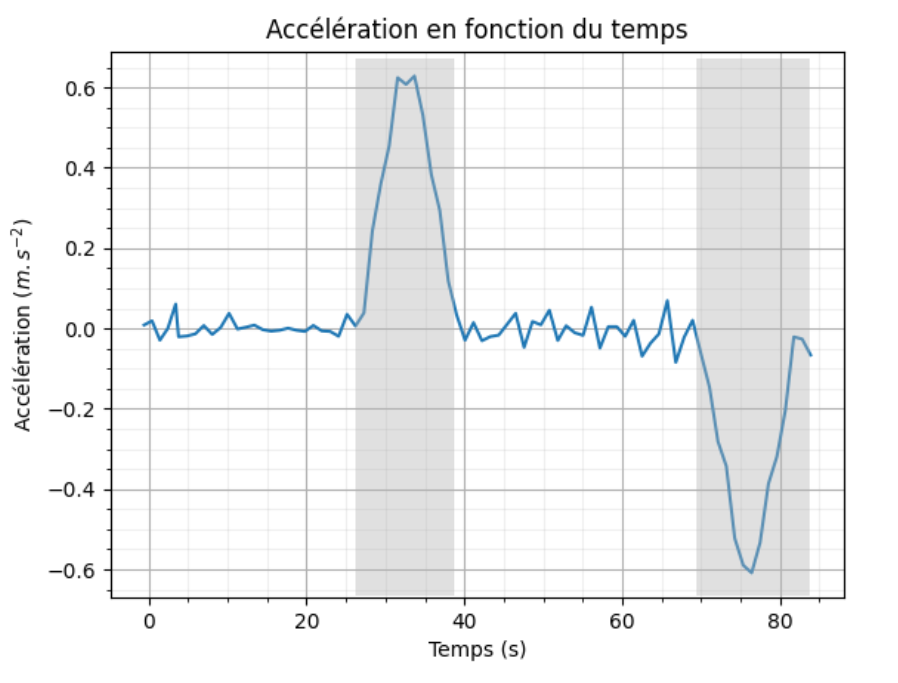
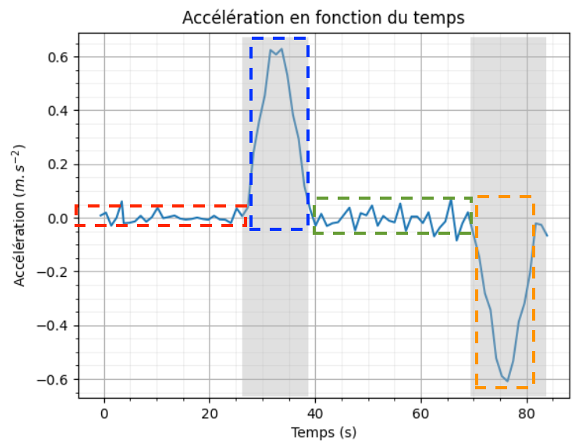
Figure 3. Évolution de la composante verticale de l’accélération de l’ascenseur lors de la montée étudiée
Q8. Décrire le mouvement de l’ascenseur dans le référentiel terrestre supposé galiléen lors des quatre phases identifiées sur la figure 2.
Lors de la phase 1, la vitesse de l’ascenseur est nulle : l’ascenseur est à l’arrêt.
Lors de la phase 2, la vitesse de l’ascenseur augmente, de plus un ascenseur ne se déplace que selon l’axe z (axe verticale) : l’ascenseur est en mouvement rectiligne accéléré.
Lors de la phase 3, la vitesse de l’ascenseur est constante, de plus un ascenseur ne se déplace que selon l’axe z (axe verticale) : l’ascenseur est en mouvement rectiligne uniforme.
Lors de la phase 4, la vitesse de l’ascenseur diminue, de plus un ascenseur ne se déplace que selon l’axe z (axe verticale) : l’ascenseur est en mouvement rectiligne décéléré.
Q9. Justifier que la courbe d’accélération donnée en figure 3 est cohérente avec ces quatre phases.
Phase 1 : l’ascenseur est à l’arrêt l’accélération est nulle.
Phase 2 : l’ascenseur est en mouvement rectiligne accéléré, l’accélération est positive.
Phase 3 : l’ascenseur est en mouvement rectiligne uniforme, l’accélération est nulle.
Phase 4 : l’ascenseur est en mouvement rectiligne décéléré, l’accélération est négative.
La courbe d’accélération donnée en figure 3 est cohérente avec ces quatre phases.
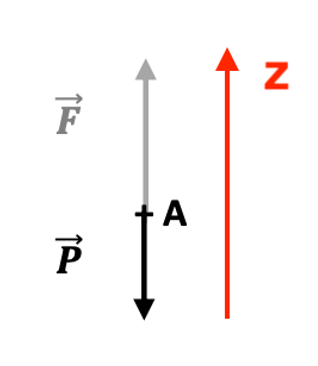
Les schémas ci-dessous représentent les forces s’exerçant sur l’ascenseur, $\overrightarrow{P}$ correspondant au poids et $\overrightarrow{F}$ à l’ensemble des autres forces verticales telles que la force élévatrice et les différentes forces de frottement (air, freinage).
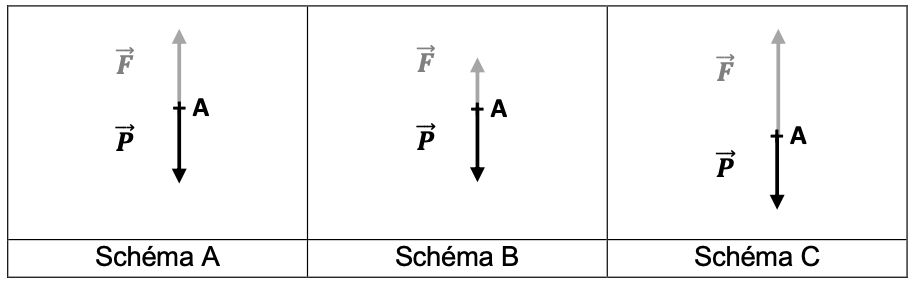
Q10. Associer, en justifiant, un schéma à chaque phase du mouvement identifiée sur la figure 2.
D’après la deuxième loi de newton :
$\Sigma\overrightarrow {F_{ext}}=m\overrightarrow{a}$
$\overrightarrow{P}+\overrightarrow{F}=m\overrightarrow{a}$
Phase 1 : l’ascenseur est à l’arrêt l’accélération est nulle.
$\overrightarrow{P}+\overrightarrow{F}=m \times \overrightarrow{0}$
$\overrightarrow{P}+\overrightarrow{F}=\overrightarrow{0}$
$\overrightarrow{P}=-\overrightarrow{F}$
Le poids $\overrightarrow{P}$ et les forces $\overrightarrow{F}$ se compensent : Schéma A
Phase 2 : l’ascenseur est en mouvement rectiligne accéléré, l’accélération est positive.
$\overrightarrow{P}+\overrightarrow{F}=m\overrightarrow{a}$
L’accélération est positive : $m\overrightarrow{a}>\overrightarrow{0}$
$\overrightarrow{P}+\overrightarrow{F}>\overrightarrow{0}$ : la somme des forces est dirigée vers le haut
La valeur des forces $\overrightarrow{F}$ dirigés (vers le haut) est supérieure à celle du poids (dirigé vers le bas) : Schéma C
Phase 3 : l’ascenseur est en mouvement rectiligne uniforme, l’accélération est nulle.
$\overrightarrow{P}+\overrightarrow{F}=m \times \overrightarrow{0}$
$\overrightarrow{P}+\overrightarrow{F}=\overrightarrow{0}$
$\overrightarrow{P}=-\overrightarrow{F}$
Le poids $\overrightarrow{P}$ et les forces $\overrightarrow{F}$ se compensent : Schéma A
Phase 4 : l’ascenseur est en mouvement rectiligne décéléré, l’accélération est négative.
$\overrightarrow{P}+\overrightarrow{F}=m\overrightarrow{a}$
L’accélération est négative : $m\overrightarrow{a}<\overrightarrow{0}$
$\overrightarrow{P}+\overrightarrow{F}<\overrightarrow{0}$ : la somme des forces est dirigée vers le bas
La valeur des forces $\overrightarrow{F}$ (dirigés vers le haut) est inférieur à celle du poids (dirigé vers le bas) : Schéma B
Q11. À l’aide de la deuxième loi de Newton et de la figure 3, estimer la valeur maximale de 𝐹, en supposant que l’ascenseur vide pèse 2,0 tonnes et qu’il peut accueillir 21 personnes.
Le candidat est évalué sur ses capacités à concevoir et à mettre en œuvre une démarche de résolution. Toutes les prises d’initiative et toutes les tentatives de résolution, même partielles, seront valorisées.
D’après la deuxième loi de newton :
$\Sigma\overrightarrow{F_{ext}}=m\overrightarrow{a}$
$\overrightarrow{P}+\overrightarrow{F}=m\overrightarrow{a}$
Projetons sur l’axe z :
$-P+F=ma$
$F=ma+P$
$F=ma+mg$
$F=m\left(a+g\right)$
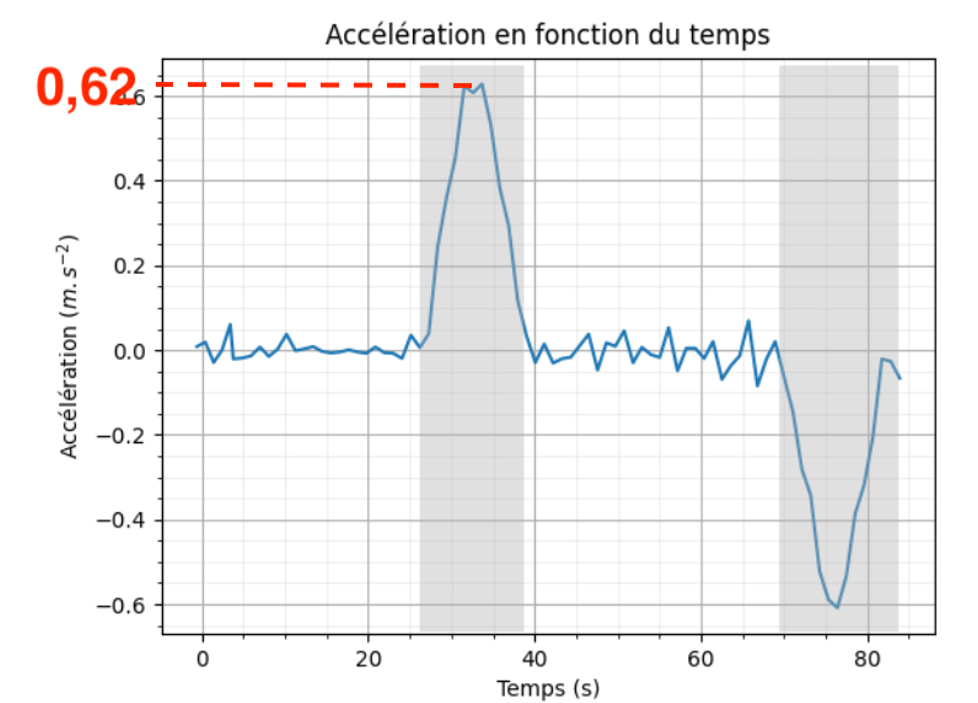
Le poids dépend uniquement du nombre de personne et l’accélération change de valeur (Figure 3). On cherche la valeur maximale de 𝐹, on prend donc la valeur maximale de l’accélération. Graphiquement $a=0,62\ m.s^{-2}$.
Considérons que chaque personne pèse environs 70 kg.
$F=m\left(a+g\right)$
$F=\left(70 \times 21+2,0{ \times 10}^3\right)\left(0,62+9,81\right)$
$F=3,6{ \times 10}^4\ N$
2. Installation de panneaux solaires
D’après la mission régionale d’autorité environnementale d’Île-de-France, la tour Montparnasse consomme aujourd’hui au total 35,75 GW∙h·an−1 .
Lors de la rénovation de la tour, on pourrait envisager de recouvrir la terrasse avec des panneaux photovoltaïques placés horizontalement.
Données :
- surface de la terrasse : 𝑆 = 1 700 m2;
- dimensions du panneau photovoltaïque rectangulaire : 1,980 m par 1,002 m ;
- caractéristiques du panneau photovoltaïque pour une irradiance 𝐼 = 1,0 kW·m-2 :
| Tension à la puissance maximale 𝑈𝑃max | 38,4 V |
| Intensité à la puissance maximale 𝐼𝑃max | 9,38 A |
- puissance du rayonnement lumineux reçue par un panneau : 𝑃ray = 𝐼 ⋅ 𝑆 où 𝐼 est l’irradiance de la lumière, en W⋅m−2 et 𝑆 la surface du panneau, en m² ;
- le rendement 𝑟 d’un panneau photovoltaïque est égal au quotient de la puissance électrique 𝑃élec générée par le panneau par la puissance rayonnante 𝑃ray reçue :
$$r = \dfrac{P_{élec}}{P_{ray}}$$
– 1 W⋅h = 3 600 J
Q12. Montrer que la puissance électrique maximale que peut fournir ce panneau photovoltaïque est proche de 360 W, pour une irradiance 𝐼 = 1,0 kW·m-2.
$P_{elec,max}=U_{Pmax} \times I_{Pmax}$
$P_{elec,max}=38,4 \times 9,38$
$P_{elec,max}=360\ W$
Q13. En déduire que le rendement du panneau est 𝑟 ≈ 18 %.
$r=\frac{P_{elec}}{P_{ray}}$
$P_{ray}=I \times S$
D’où
$r=\frac{P_{elec}}{I \times S}$
Or
$S=l \times L$
D’où
$r=\frac{P_{elec}}{I \times l \times L}$
$r=\frac{360}{1,0{ \times 10}^3 \times 1,980 \times 1,002}$
$r=0,18$
$r=18\ %$
À Paris, l’énergie rayonnante solaire annuelle moyenne est d’environ 1 300 kW·h·m-2.
Q14. Estimer, avec la valeur du rendement du panneau déterminée à la question Q13, la valeur de l’énergie électrique que pourrait fournir l’installation de panneaux sur l’ensemble de la terrasse de la tour en une année. Commenter.
À Paris, l’énergie rayonnante solaire annuelle moyenne est d’environ 1 300 kW·h·m-2.
Calculons l’énergie total reçue si toute la terrasse (𝑆 = 1 700 m2) était couverte de panneaux photovoltaïques :
$1\ 300\ kW·h\quad1\ m^2$
$E_{total\ recue}\quad1\ 700\ m^2$
$E_{total\ recue}=\frac{1\ 700 \times 1300}{1}$
$E_{total\ recue}=2,2{ \times 10}^6\ kW\bullet h$
Calculons l’énergie électrique produite :
$r=\frac{E_{elec}}{E_{total\ recue}}$
$\frac{E_{elec}}{E_{total\ recue}}=r$
$E_{elec}=r \times E_{total\ recue}$
$E_{elec}=\frac{18}{100} \times 2,2{ \times 10}^6$
$E_{elec}=4,0{ \times 10}^5\ kW\cdot h$
$E_{elec}=4,0{ \times 10}^8\ W\cdot h$
Calculons le pourcentage que cette énergie représente par rapport à l’énergie nécessaire à la tour Montparnasse :
$P=\frac{E_{elec}}{E_{tour}}$
$P=\frac{4,0{ \times 10}^8}{35,75{ \times 10}^9}$
$P=0,011$
$P=1,1\ %$
L’énergie solaire produite ne représenterait que 1,1 % des besoins annuels de la tour : c’est très faible.
3. Rénovation énergétique de la tour Montparnasse.
La surface vitrée de la tour Montparnasse est d’environ 40 000 m2. Les fenêtres de la tour sont en simple vitrage dont l’épaisseur est de 4 mm de verre. Elles vont être remplacées par des fenêtres à double vitrage pour augmenter la performance énergétique du bâtiment.
Données :
– la résistance thermique de conduction 𝑅 (en K⋅W-1) d’un matériau est liée aux grandeurs 𝑒, λ et 𝑆 par la relation :
La résistance thermique :
$$R_c = \dfrac{e}{S \times \lambda}$$
λ : conductivité thermique du matériau en W⋅m-1⋅K-1;
e : épaisseur de la paroi en m ;
S : surface de la paroi en m2 ;
– conductivité thermique de divers matériaux :
| Matériau | air au repos | verre | bois | PVC | aluminium |
| Conductivité thermique l (W⋅m-1⋅K-1) | 0,026 | 1,0 | 0,13 | 0,17 | 185 |
Q15. Citer les trois modes de transfert thermique.
Un transfert thermique peut avoir lieu par conduction, convection ou rayonnement.
Dans la modélisation suivante, on considère qu’une fenêtre est exclusivement constituée par son vitrage. La conductivité thermique du cadre est négligée.
Q16. Calculer la valeur de la résistance thermique de conduction 𝑅c pour une surface de 1,00 m2 de simple vitrage.
$R_c=\frac{e}{S \times \lambda}$
$R_c=\frac{4{ \times 10}^{-3}}{1,00 \times 1,0}$
$R_c=4{ \times 10}^{-3}\ K.W^{-1}$
La résistance thermique globale 𝑅g modélise l’ensemble des transferts thermiques du vitrage. Elle est liée au coefficient de transmission thermique $U_g = \dfrac{1}{R_g \times S}$ dont la valeur pour ce vitrage est égale à $ = 5,75\ \text{W.m}^{-2}\text{.K}^{-1}$.
Q17. Calculer la valeur de la résistance thermique globale 𝑅g pour une surface de vitrage de 1,00 m2. Commenter.
$U_g=\frac{1}{R_g \times S}$
$U_g{ \times R}_g=\frac{1}{S}$
$R_g=\frac{1}{U_g \times S}$
$R_g=\frac{1}{5,75 \times 1,00}$
$R_g=1,7{ \times 10}^{-1}\ \ K.W^{-1}$
$R_g \gg R_c$
La résistance thermique globale est beaucoup plus grande que la résistance par simple conduction du verre seul
Ainsi, les pertes thermiques d’une fenêtre ne sont pas dues seulement à la conduction dans le verre.
On considère que la température à l’intérieur de la tour Montparnasse est maintenue constante à 20,0 °C. L’analyse des données publiques de Météo France montre que la température extérieure a été inférieure à 20,0 °C pendant 279 jours à Paris en 2023. La température extérieure moyenne durant cette période a été de 11,3 °C.
Q18. Déterminer la valeur du flux thermique à travers une surface 𝑆 = 1,00 m2 de fenêtre à simple vitrage pour une température de 11,3 °C.
$\phi_{simple}=\frac{\Delta \theta}{R_g}$
$\phi_{simple}=\frac{20,0-11,3}{1,7{ \times 10}^{-1}}$
$\phi_{simple}=51\ W$
Q19. Estimer l’énergie économisée sur une année en GW·h si on remplace le simple vitrage par du double vitrage de coefficient $U_{g\ double} = 1,15\ \text{W.m}^{-2}\text{.K}^{-1}$
n utilisant les données météorologiques de 2023.. Commenter.
Le candidat est évalué sur ses capacités à concevoir et à mettre en œuvre une démarche de résolution. Toutes les prises d’initiative et toutes les tentatives de résolution, même partielles, seront valorisées.
$\phi_{double}=\frac{\Delta \theta}{R_g\ double}$
Or
$U_{g\ double}=\frac{1}{R_{g\ double} \times S}$
$U_{g\ double} \times R_{g\ double}=\frac{1}{S}$
$R_{g\ double}=\frac{1}{U_{g\ double} \times S}$
D’où
$\phi_{double}=\frac{\Delta\theta}{\frac{1}{U_{g\ double} \times S} }$
$\phi_{double}=\Delta\theta \times U_{g\ double} \times \frac{S}{1}$
$\phi_{double}=\Delta\theta \times U_{g\ double} \times S$
$\phi_{double}=\left(20,0-11,3\right) \times 1,15 \times 1,00$
$\phi_{double}=10\ W$
Flux économisé :
$\phi_{economise}=\phi_{simple}-\phi_{double}$
$\phi_{economise}=51-10$
$\phi_{economise}=41\ W$
Calculons la puissance économisée pour toute la surface des fenêtres :
| 41 W | 1 m2 |
| Peconomise | 40 000 m2 |
$P_{economise}=\frac{40\ 000\ \times 41}{1}$
$P_{economise}=1,6{ \times 10}^6\ W$
Calculons l’énergie économisée :
$E_{economise}=P_{economise} \times \Delta t$
$E_{economise}=1,6{ \times 10}^6\ \times 279 \times 24$
$E_{economise}=1,1{ \times 10}^{10}\ W\bullet h$
Calculons le pourcentage que cette énergie représente par rapport à l’énergie nécessaire à la tour Montparnasse :
$P=\frac{E_{economise}}{E_{tour}}$
$P=\frac{1,1{ \times 10}^{10}}{35,75{ \times 10}^9}$
$P=0,31$
$P=31\ %$
L’énergie économisé représenterait 31 % des besoins annuels de la tour : c’est non négligeable.
