Cargo dirigeable

Bac Amérique du sud 2025 Sujet 2

Exercice 3 – (5 points) –  Durée 0h53 – Calculatrice autorisée

Sujet n°25-PYCJ2AS1

Dirigeable

www.flying-whales.com

L’objectif de cet exercice est de vérifier la charge maximale embarquable dans un dirigeable et d’étudier un système permettant d’effectuer un chargement en vol stationnaire.

Caractéristiques du dirigeable étudié :

• volume du dirigeable : 𝑉 = 180 000 m³ ;
• masse du dirigeable avant remplissage en gaz porteur : 𝑚_d = 65 tonnes.

Partie 1. Étude de la charge maximale embarquée Données :

• masse molaire de l’hélium : 𝑀_He = 4,0 g⋅mol^-1 ;
• constante des gaz parfaits : 𝑅 = 8,314 J·K^-1·mol^-1 ;
• conversion entre les échelles de température : 𝑇(K) = 𝜃(°C) + 273 ;
• 1,0 bar = 1,0 × 10⁵ Pa ;
• intensité de la pesanteur : 𝑔 = 9,8 m∙s^-2 .

On fait l’hypothèse que le dirigeable a été entièrement rempli d’hélium, se comportant comme un gaz parfait, sous une pression de 𝑃 = 1,1 bar et à la température 𝜃 = 25 °C.

Q1.    Montrer que la valeur de la masse d’hélium embarqué dans le dirigeable est proche de 𝑚_He = 32 tonnes.

$n_{He}=\frac{m_{He}}{M_{He}}$
$\frac{m_{He}}{M_{He}}=n_{He}$
$m_{He}=n_{He}\times M_{He}$

Or
$P\times V=n_{He}\times R\times T$
$n_{He}\times R \times T=P \times V$
$n_{He}=\frac{P\times V}{R\times T}$

D’où
$m_{He}=\frac{P\times V}{R\times T}\times M_{He}$

Or
$T=\theta+273$

D’où
$m_{He}=\frac{P\times V}{R\times \left(\theta+273\right)}\times M_{He}$
$m_{He}=\frac{1,1\times {10}^5\times180\ 000}{8,314\times \left(25+273\right)}\times 4,0$
$m_{He}=3,2\times {10}^7g$
$m_{He}=3,2\times {10}^4\ kg$
$m_{He}=3,2\times {10}^1\ tonnes$
$m_{He}=32\ tonnes$

Q2.    Parmi les relations suivantes, choisir, en justifiant, celle donnant l’expression vectorielle de la poussée d’Archimède $\overrightarrow{P_a}$ exercée par l’air sur le dirigeable.
$\overrightarrow{P_a} = \rho_{\text{air}} \cdot V \cdot \overrightarrow{g}$
$\overrightarrow{P_a} = m_{\text{air}} \cdot V \cdot \overrightarrow{g}$
$\overrightarrow{P_a} = -\rho_{\text{air}} \cdot V \cdot \overrightarrow{g}$

Faisons une analyse dimensionnelle des expressions proposées :

Remarque une force s’exprime en Newton.
D’après la deuxième loi de newton :
$\Sigma\vec{F_{ext}}=m\vec{a}$
$\left[\Sigma\vec{F_{ext}}\right]=\left[m\right]\left[\vec{a}\right]$
$N=Kg\bulletm\cdot s^{-2}$

Expression 1 :
$\vec{P_A}=\rho_{air}\times V\times \vec{g}$
$P_A=\rho_{air}\times V\times g$
$[P_A]=\left[\rho_{air}\right]\times \left[V\right]\times \left[g\right]$
$N=Kg\cdot m^3\times  m^{-3}\times m\cdot s^{-2}$
$N=Kg \bullet m\cdot s^{-2}$
Cette expression est homogène.

Expression 2 :
$\vec{P_A}=m_{air}\times V\times \vec{g}$
$P_A=m_{air}\times V\times g$
$[P_A]=\left[m_{air}\right]\times \left[V\right]\times \left[g\right]$
$N=Kg\times  m^{-3}\times m\cdot s^{-2}$
$N=Kg\cdot m^{-2}\cdot s^{-2}$
Cette expression n’est pas homogène.

Expression 3 :
$\vec{P_A}=-\rho_{air}\times V\times \vec{g}$
$P_A=\rho_{air}\times V\times g$
$[P_A]=\left[\rho_{air}\right]\times \left[V\right]\times \left[g\right]$
$N=Kg\cdot m^3\times  m^{-3}\times m\cdot s^{-2}$
$N=Kg\bulletm\cdot s^{-2}$
Cette expression est homogène.

A l’aide de l’analyse dimensionnel nous avons retiré l’expression 2.

La poussée d’Archimède dirigée vers le haut.

Expression 1 : $\vec{P_A}=\rho_{air}\times V\times \vec{g}$ ici $\vec{P_A}$ est dans le sens du vecteur champs de pesanteur soit vers le bas. Nous éliminons l’expression 1.

Expression 3 : $\vec{P_A}={-\rho}_{air}\times V\times \vec{g}$ ici $\vec{P_A}$ est dans le sens opposé du vecteur champs de pesanteur soit vers le haut. Nous conservons l’expression 3.

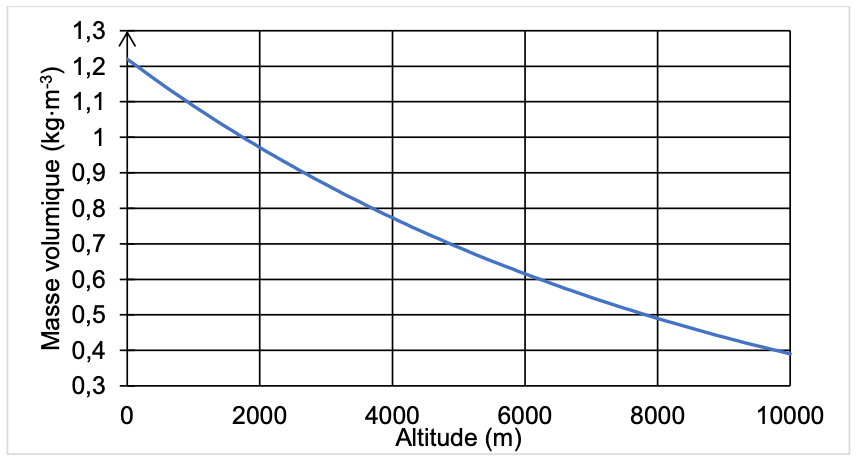
Figure 1. Représentation de l’évolution de la masse volumique de l’air en fonction de l’altitude

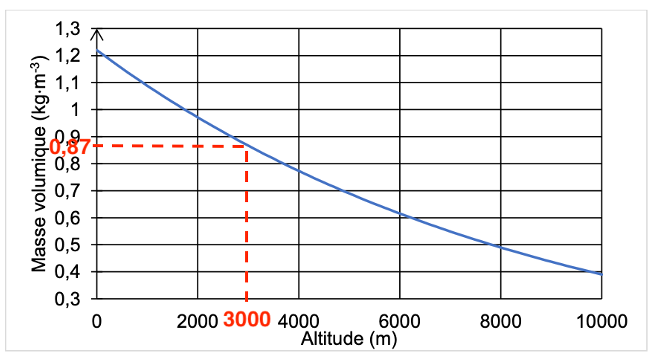
Q3. Calculer la valeur de la poussée d’Archimède exercée par l’air sur le dirigeable à une altitude de 3000 m.

Q4. Préciser comment l’intensité de cette force évolue en fonction de l’altitude. On étudie le système {dirigeable} dans le référentiel terrestre supposé Galiléen.

$P_A=\rho_{air}\times V\times g$
La poussée d’Archimède est proportionnelle à $\rho_{air}$.
D’après la figure 1, la masse volumique de l’air $\rho_{air}$ diminue quand l’altitude augmente.

Ainsi, l’intensité de la poussée d’Archimède diminue quand l’altitude augmente.

Q5. À l’aide d’une des lois de Newton que l’on citera, déterminer la relation entre le poids $\overrightarrow{P}$ du système et la poussée d’Archimède $\overrightarrow{P_a}$ qu’il subit lorsqu’il vole en ligne droite, à altitude et vitesse constante.

Système {dirigeable}
Référentiel terrestre supposé galiléen

Le système vole en ligne droite, à altitude et vitesse constante : il a un mouvement rectiligne uniforme.
D’après la 1^ere loi de Newton :
$\Sigma\vec{F_{ext}}=\vec{0}$
$\vec{P}+\vec{P_A}=\vec{0}$

Q6. Vérifier que la charge maximale transportable par ce dirigeable à 3000 m d’altitude est proche de 60 tonnes.

$\vec{P}+\vec{P_A}=\vec{0}$
$\vec{P}=-\vec{P_A}$
Le poids 𝑃 du système et la poussée d’Archimède 𝑃𝑎 se compensent : ils ont la meme valeur, la meme direction et un sens opposé.
$P=P_A$
Or
$P=mg$

$mg=P_A$
$m=\frac{P_A}{g}$
$m=\frac{1,5\times {10}^6\ }{9,8}$
$m=1,5\times {10}^5\ Kg$
$m=1,5\times {10}^2\ tonnes$
Cette masse est la masse totale.

or :
la masse du dirigeable avant remplissage en gaz porteur : 𝑚d = 65 tonnes.
la masse d’hélium embarqué dans le dirigeable est proche de 𝑚He = 32 tonnes.

$m=m_d+m_{He}+m_{charge}$
$m_d+m_{He}+m_{charge}=m$
$m_{charge}=m-m_d-m_{He}$
$m_{charge}=1,5\times {10}^2-65-32$
$m_{charge}=53\ tonnes$

Ainsi, la charge maximale transportable par ce dirigeable à 3000 m d’altitude est proche de 60 tonnes.

Remarque : en ne faisant pas de calcul intermédiaire, on fait moins d’arrondis à cause des règles des chiffres significatifs et on tombe sur 60 tonnes :
$m_{charge}=m-m_d-m_{He}$
$m_{charge}=\frac{P_A}{g}-m_d-m_{He}$
$m_{charge}=\frac{\rho_{air}\times V\times g}{g}-m_d-m_{He}$
$m_{charge}=0,87\times 180\ 000-65\times {10}^3-32\times {10}^3$
$m_{charge}=6,0\times {10}^4\ kg$
$m_{charge}=60\ tonnes$

Partie 2. Chargement d’un tronc d’arbre

Un des défis à résoudre pour le transport de charge lourde est de pouvoir charger ou décharger le dirigeable en vol stationnaire, en quelques minutes.

Une des solutions technologiques envisagée est un transfert d’eau. À son départ, le dirigeable possède un réservoir rempli d’eau. Pour embarquer la charge en vol stationnaire, le dirigeable vide son réservoir d’une masse d’eau équivalente à la masse de la charge afin de rester fixe par rapport au sol.

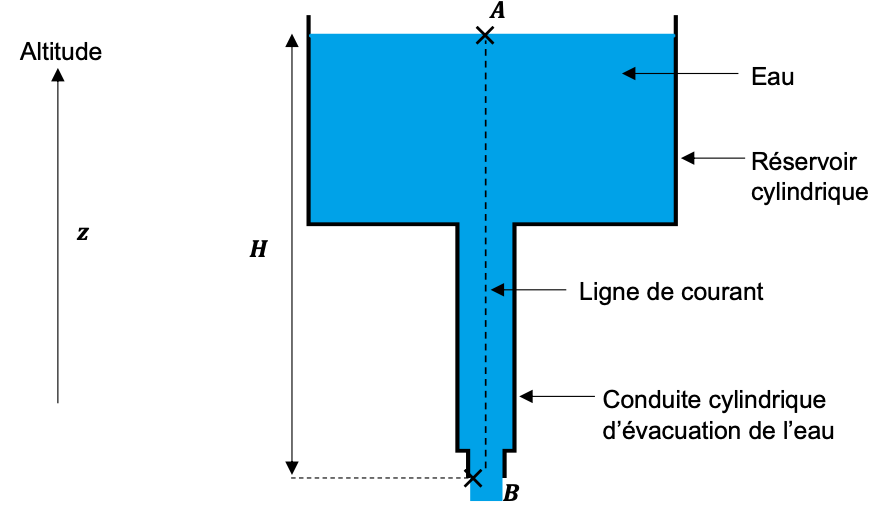
Figure 2. Schéma de principe du réservoir d’eau embarqué dans le dirigeable.

Données :

• diamètre du réservoir en 𝐴 : 𝑑_𝐴 = 3,0 m ;
• diamètre du conduit au niveau de la sortie d’eau en 𝐵 : 𝑑_𝐵 = 15 cm ;
• masse volumique de l’eau : 𝜌_eau = 1000 kg∙m^-3 ;
• hauteur 𝐻 entre les points 𝐴 et 𝐵 : 𝐻 = 30 m ;
• l’écoulement d’un fluide incompressible en régime permanent peut être modélisé par la relation de Bernoulli. Sur une ligne de courant :

$$P + \dfrac{1}{2} \cdot \rho \cdot v^2 + \rho \cdot g \cdot z = \text{constante}$$

avec 𝑃 la pression du fluide (en Pa), 𝜌 la masse volumique du fluide (en kg∙m^-3), 𝑣 la vitesse d’écoulement du fluide (en m∙s^-1) et 𝑧 l’altitude (en m) ;

• dans une conduite, la relation entre le débit volumique 𝐷_𝑉 (en m³∙s^-1), la vitesse d’écoulement 𝑣 (en m∙s^-1) d’un fluide incompressible en régime permanent et 𝑆 l’aire de la section du conduit (en m²) est donnée par :

𝐷_𝑉 = 𝑣 ∙ 𝑆

L’eau sera considérée comme un fluide incompressible, son écoulement s’effectue en régime permanent.

Q7. En exploitant la conservation du débit volumique, montrer que la vitesse d’écoulement 𝑣A au point A est négligeable par rapport à la vitesse d’écoulement 𝑣_B au point B.

Conservation du débit volumique :
$D_{V(B)}=D_{V(A)}$
$S_B\times v_B=S_A\times v_A$
$\frac{v_B}{v_A}=\frac{S_A}{S_B}$
$\frac{v_B}{v_A}=\frac{\pi\times r_A^2}{\pi\times r_B^2}$
$\frac{v_B}{v_A}=\frac{r_A^2}{r_B^2}$
$\frac{v_B}{v_A}=\frac{\left(\frac{d_A}{2}\right)^2}{\left(\frac{d_B}{2}\right)^2}$
$\frac{v_B}{v_A}=\left(\frac{\frac{d_A}{2}}{\frac{d_B}{2}}\right)^2$
$\frac{v_B}{v_A}=\left(\frac{d_A}{2}\times \frac{2}{d_B}\right)^2$
$\frac{v_B}{v_A}=\left(\frac{d_A}{d_B}\right)^2$
$\frac{v_B}{v_A}=\left(\frac{3,0}{15\times {10}^{-2}}\right)^2$
$\frac{v_B}{v_A}=400$

Ainsi, la vitesse d’écoulement 𝑣B au point B est 400 fois plus grande que la vitesse d’écoulement 𝑣A au point A.
La vitesse d’écoulement 𝑣A au point A est donc négligeable par rapport à la vitesse d’écoulement 𝑣B au point B.

Q8. En appliquant la relation de Bernoulli sur la ligne de courant entre les points A et B et sachant que les pressions du fluide en A et B sont égales à la pression atmosphérique, montrer que la vitesse d’écoulement 𝑣B du fluide en 𝐵 est donnée par l’expression :

$$v_B = \sqrt{2 \cdot g \cdot H}$$

Relation de Bernoulli dans la conduite horizontale :
$P+\frac{1}{2}\times \rho\times v^2+\rho\times g\times z=constante$
$P_B+\frac{1}{2}\times \rho\times v_B^2+\rho\times g\times z_B=P_A+\frac{1}{2}\times \rho\times v_A^2+\rho\times g\times z_A$

Or la vitesse d’écoulement 𝑣A au point A est donc négligeable par rapport à la vitesse d’écoulement 𝑣B au point B.
$P_B+\frac{1}{2}\times \rho\times v_B^2+\rho\times g\times z_B=P_A+\rho\times g\times z_A$
$\frac{1}{2}\times \rho\times v_B^2=P_A-P_B+\rho\times g\times z_A-\rho\times g\times z_B$
$\frac{1}{2}\times \rho\times v_B^2=P_A-P_B+\rho\times g\times \left(z_A-z_B\right)$

Or $P_B=P_A=P_{atmospherique}$
$\frac{1}{2}\times \rho\times v_B^2=P_{atmospherique}-P_{atmospherique}+\rho\times g\times \left(z_A-z_B\right)$
$\frac{1}{2}\times \rho\times v_B^2=\rho\times g\times \left(z_A-z_B\right)$
$v_B^2=\frac{2\times \rho\times g\times \left(z_A-z_B\right)}{\rho}$
$v_B^2=2\times g\times \left(z_A-z_B\right)$

Or $z_A-z_B\ =\ H$

$v_B^2=2\times g\times H$
$v_B=\sqrt{2\times g\times H}$

On envisage la charge d’un morceau de bois de 𝑚_bois = 8 tonnes.

Q9. Déterminer la durée minimale nécessaire pour la vidange de l’eau nécessaire au chargement de ce morceau de bois dans le dirigeable. Commenter le résultat obtenu.

Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et doit être correctement présentée.

On envisage la charge d’un morceau de bois de $m_{bois} = 8\ \text{tonnes}$.
Il faut donc vider $m_{eau} = 8\ \text{tonnes}$.

$\rho_{eau}=\dfrac{m_{eau}}{V_{eau}}$
$\rho_{eau}\times  V_{eau}=m_{eau}$
$V_{eau}=\dfrac{m_{eau}}{\rho_{eau}}$
$V_{eau}=\dfrac{8\times  10^3}{1000}$
$V_{eau}=8\ m^3$

Calculons la hauteur d’eau correspondante :
$V_{eau}=S_A\times  h_{eau}$
$S_A\times  h_{eau}=V_{eau}$
$h_{eau}=\dfrac{V_{eau}}{S_A}$
$h_{eau}=\dfrac{V_{eau}}{\pi\times  r_A^2}$
$h_{eau}=\dfrac{V_{eau}}{\pi\times \left(\dfrac{d_A}{2}\right)^2}$
$h_{eau}=\dfrac{8}{\pi\times \left(\dfrac{3}{2}\right)^2}$
$h_{eau}=1,1\ m$

La hauteur d’eau correspondante est petite devant la hauteur d’eau initiale $H=30\ m$ : on peut donc considérer que la hauteur $H$ ne varie pas au cours de cette vidange.
$v_B=\sqrt{2\times  g\times  H}$
$v_B=\sqrt{2\times  9,8\times  30}$
$v_B=24\ m.s^{-1}$

$D_{V(B)}=\dfrac{V_{eau}}{\Delta t}$

Or
$D_{V(B)}=S_B\times  v_B$

Ainsi
$S_B\times  v_B=\dfrac{V_{eau}}{\Delta t}$
$S_B\times  v_B\times  \Delta t=V_{eau}$
$\Delta t=\dfrac{V_{eau}}{S_B\times  v_B}$
$\Delta t=\dfrac{V_{eau}}{\pi\times  r_B^2\times  v_B}$
$\Delta t=\dfrac{V_{eau}}{\pi\times \left(\dfrac{d_B}{2}\right)^2\times  v_B}$
$\Delta t=\dfrac{8}{\pi\times \left(\dfrac{15\times  10^{-2}}{2}\right)^2\times  24}$
$\Delta t=19\ s$

La durée minimale nécessaire pour la vidange de l’eau nécessaire au chargement de ce morceau de bois dans le dirigeable est de 19 s.