Observation d’un volcan par interférométrie satellitaire radar

Bac Amérique du nord 2024 Sujet 1

Exercice 1 – (11 points) –  Durée 1h56 – Calculatrice autorisée

Sujet n°24-PYCJ1AN1

Sujet et corrigé

EXERCICE 1 : observation d’un volcan par interférométrie satellitaire radar (11 points)

Image de synthèse (earth.esa.int/eogateway/missions/alos)

Données :

• masse de la Terre : M_T = 5,97×10²⁴ kg ;
• rayon de la Terre : R_T = 6,37×10⁶ m ;
• constante de gravitation universelle : G = 6,67×10^–11 m³∙kg^-1∙s^-2 ;
• la valeur de la vitesse de propagation des ondes électromagnétiques dans le vide, notée c, est supposée connue.

1.    Étude du mouvement orbital du satellite ALOS

ALOS est placé sur une orbite polaire (c’est-à-dire passant à la verticale des pôles terrestres) supposée circulaire dans le référentiel géocentrique à une altitude h = 692 km. Le satellite se déplace à une vitesse proche de 2,7 x 10⁴ km·h^-1.

En utilisant les données d’altitude et de période du satellite, un programme écrit en langage python (voir figure 1) a permis de déterminer les positions du satellite sur son orbite à intervalle de temps régulier Δt = 369,3 s et de représenter les vecteurs vitesse et variation de vitesse du satellite en ces points (figure 2).

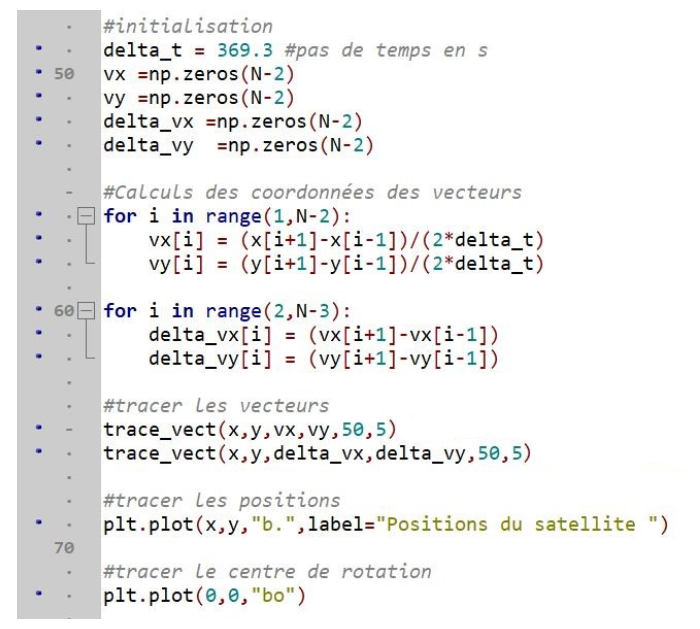
Figure 1 : programme en langage python

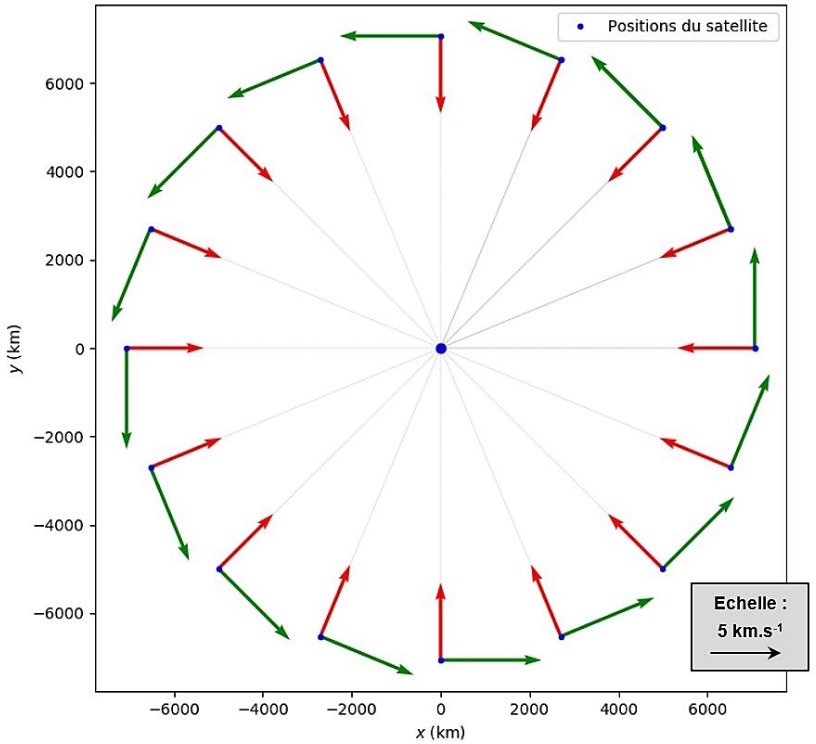
Figure 2 : vecteurs tracés après exécution du programme

Q.1. Indiquer les lignes du programme fourni qui permettent de calculer les coordonnées approchées des vecteurs variation de vitesse.

Les lignes du programme fourni qui permettent de calculer les coordonnées approchées des vecteurs variation de vitesse sont les lignes 60, 61 et 62.

Q.2. Indiquer lequel des deux vecteurs représentés à une position du satellite donnée sur la figure 2 correspond au vecteur variation de vitesse. Justifier.

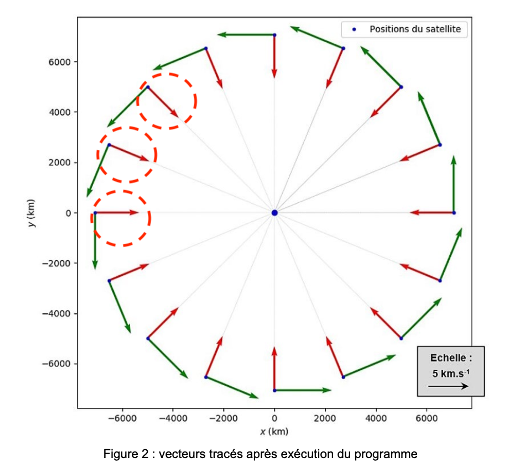
Méthode 2 :
D’après la 2nd loi de Newton :
$\Sigma\overrightarrow{F_{ext}}=m\overrightarrow{a}$
$\Sigma\overrightarrow{F_{ext}}=m\frac{d\overrightarrow{v}}{dt}$

Ainsi le vecteur variation de vitesse a le même sens et la même direction que le vecteur $\Sigma\overrightarrow{F_{ext}}$. Or la force ici présente est la force gravitationnelle qui est radiale et centripète.
Ainsi le vecteur variation de vitesse est radial et centripète (en rouge sur le schéma).

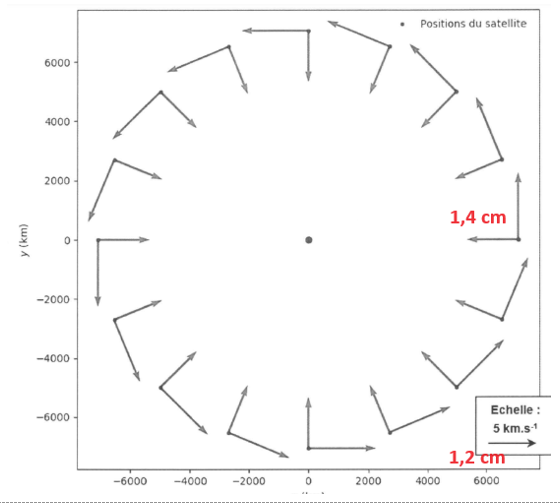
Q.3. Montrer à l’aide de l’échelle fournie sur la figure 2 que la valeur de l’accélération moyenne du satellite est voisine de 8 m·s^-2.

Le mouvement du centre de masse, S, du satellite ALOS est étudié dans le référentiel géocentrique supposé galiléen en utilisant le repère de Frenet $ (S,\ \overrightarrow{u_t},\ \overrightarrow{u_n}) $. La masse du satellite est notée m.

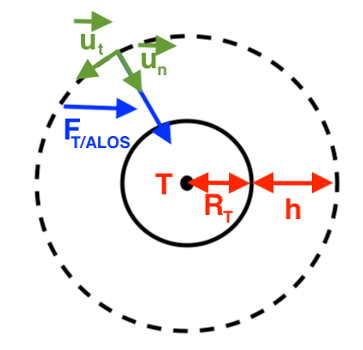
Q.4. Exprimer, dans le repère de Frenet, la force d’interaction gravitationnelle exercée par la Terre sur le satellite ALOS en fonction de G, m, M_T, R_T, h. Représenter, sans souci d‘échelle, cette force sur un schéma avec le repère de Frenet associé au satellite.

Q.5. Établir l’expression du vecteur accélération du satellite et calculer sa norme. Comparer à la valeur obtenue à la question Q.3.

Système : Satellite ALOS
Référentiel : géocentrique supposé galiléen.

D’après la 2nd loi de Newton :

$\Sigma\overrightarrow{F_{ext}}=m\overrightarrow{a}$

$\overrightarrow{F_{T/ALOS}}=m\overrightarrow{a}$

$G\times\frac{m\times M_T}{\left(R_T+h\right)^2}\overrightarrow{u}_N=m\overrightarrow{a}$

$\overrightarrow{a}=G\times\frac{M_T}{\left(R_T+h\right)^2}\overrightarrow{u}_N$

$a=G\times\frac{M_T}{\left(R_T+h\right)^2}$
$a=6,67\times{10}^{-11}\times\frac{5,97\times{10}^{24}}{\left(6,37\times{10}^6+692\times{10}^3\right)^2}$
$a=7,98\ m.s^{-2}$

Cette valeur est proche de celle annoncée dans la question Q.3.

Q.6. Montrer que le mouvement du satellite est uniforme et établir l’expression de sa vitesse :

$$ v=\sqrt{\frac{G\times M_T}{R_T+h}} $$

Pour un mouvement circulaire, dans le repère de Frenet, le vecteur accélération est de la forme :
$$
\overrightarrow{a}=\frac{v^2}{R_T+h}\overrightarrow{u}_N+\frac{dv}{dt}\overrightarrow{u}_T
$$

L’accélération étant unique, par identification :
$\frac{d\overrightarrow{v}}{dt}=\overrightarrow{0}$ donc la vitesse est constante : le mouvement est uniforme
$\frac{v^2}{R_T+h}=G\times\frac{M_T}{\left(R_T+h\right)^2}$

$v^2=G\times\frac{M_T}{R_T+h}$
$v=\sqrt{G\times\frac{M_T}{R_T+h}}$
$v=\sqrt{\frac{G\times M_T}{R_T+h}}$

Q.7. En déduire l’expression de la période de révolution du satellite en fonction de G, M_T, R_T, h. Calculer sa valeur.

La période de révolution est :
$$
T=2\pi\sqrt{\frac{\left(R_T+h\right)^3}{G\times M_T}}
$$

$T=2\pi\sqrt{\frac{\left(6,37\times{10}^6+692\times{10}^3\right)^3}{6,67\times10^{-11}\times5,97\times{10}^{24}}}$
$T=5,91\times10^3\ s$

Compte tenu de la rotation de la Terre sur elle-même, le satellite repasse tous les 46 jours à la verticale d’un même point de la surface terrestre.

Q.8. Déterminer le nombre d’orbites parcourues par le satellite ALOS avant de repasser au- dessus du même point.

Nombre de tours	Temps (s)
1
N

$N=\frac{3,97\times{10}^6}{5,91\times10^3}$
$N=672\ tours$

Le satellite ALOS parcourt 672 orbites avant de repasser au-dessus du même point.

2.    Étude de la déformation du sol par interférométrie radar

Un satellite faisant de l’interférométrie radar est dit actif : il éclaire lui-même un point de la surface terrestre qu’il observe en émettant une onde radar et récupère le signal renvoyé.

L’interférométrie satellitaire radar (InSAR) est une technique d’imagerie utilisée principalement pour détecter des mouvements de terrain comme la contraction ou le gonflement des sols argileux et le suivi de l’activité des volcans.

Q.9. Écrire la relation entre la longueur d’onde, la célérité et la période de l’onde, en précisant les unités de ces grandeurs.

$c=\frac{\lambda}{T}$

Avec :

• c en m.s^-1
• λ en mètre
• T en secondes

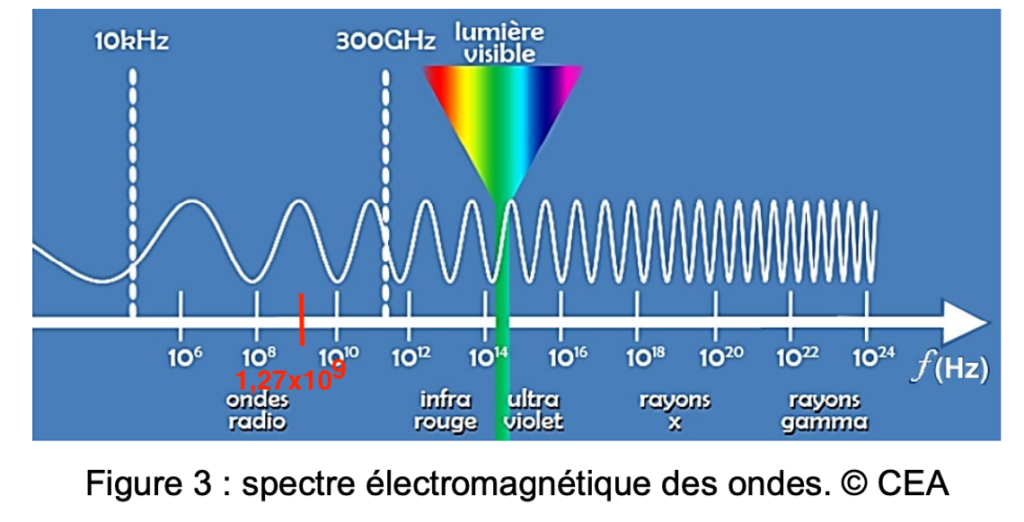
Q.10. Justifier, à l’aide du document ci-dessous, que les ondes émises par le satellite ALOS dont la longueur d’onde est 23,6 cm appartiennent au domaine des ondes radio.

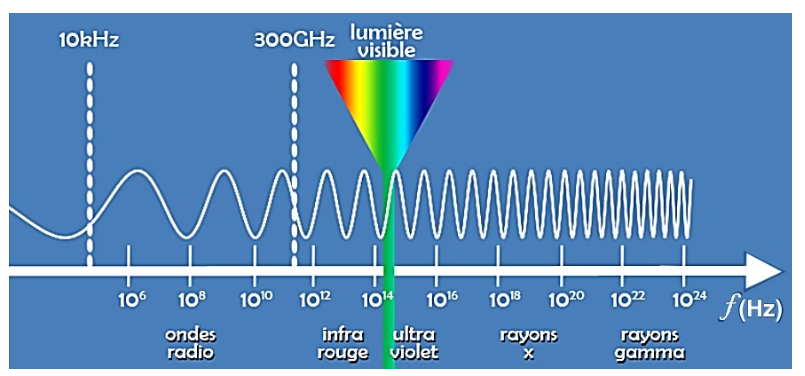
Figure 3 : spectre électromagnétique des ondes. © CEA

$c=\frac{\lambda}{T}$
or
$f=\frac{1}{T}$

Ainsi :
$c=\lambda\times f$
$\lambda\times f=c$
$f=\frac{c}{\lambda}$
$f=\frac{3,00\times{10}^8}{23,6\times{10}^{-2}}$
$f=1,27\times{10}^9\ Hz$

Le principe de la mesure de déplacement par InSAR est le suivant : le satellite capte une image de l’ensemble des points d’une même zone de la Terre depuis la même position dans le ciel à deux dates différentes (voir figure 4).

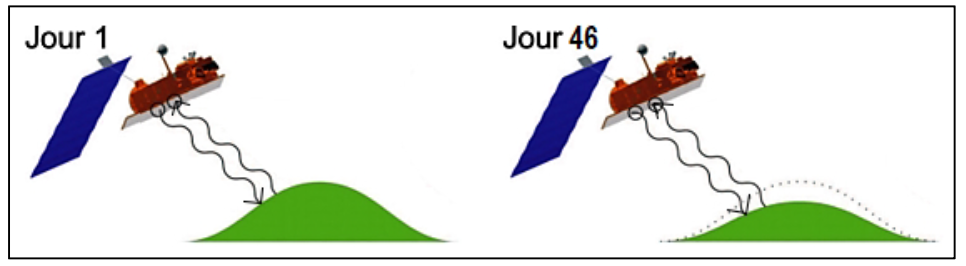
Figure 4 : trajets de l’onde émise par le satellite ALOS, pour un point de la zone étudiée

Une contraction ou un gonflement du sol survenant entre ces deux dates induit une variation de la distance entre le satellite et le sol. Cette variation génère une différence de marche entre les deux ondes radar reçues. Une figure d’interférences, appelée interférogramme, est obtenue par traitement informatique.

L’interférogramme réalisé permet de mesurer le déplacement du sol dans l’axe de visée du satellite.

On admettra que la variation d’altitude du sol est due uniquement à une contraction de ce dernier.

On note L la distance entre le satellite et le point visé à la surface de la Terre lors du premier passage et d le déplacement du sol dans l’axe de visée du satellite entre le premier et le deuxième passage du satellite.

Q.11. En exprimant la distance parcourue par l’onde radar lors du premier passage et celle parcourue par l’onde lors du deuxième passage, établir que la relation entre la différence de marche 𝛿𝛿 entre ces deux ondes et le déplacement du sol d est :

δ = 2 d

$\delta=d_2-d_1$
La distance parcourue $d_1$ est un aller-retour soit $2L$
La distance parcourue $d_2$ est un aller-retour soit $2(L+d)$

$\delta=2\left(L+d\right)-2L$
$\delta=2d$

Q.12. En déduire que la relation entre le déplacement du sol d et la longueur d’onde λ pour que ces deux ondes soient en phase est :

$d=k\times\frac{\lambda}{2}$ avec k entier

Pour que ces deux ondes soient en phase, la différence de marche doit être du type :
$\delta=k\times\lambda$

Ainsi
$2d=k\times\lambda$
$$
d=k\times\frac{\lambda}{2}
$$

Du 30 mars au 1^er avril 2007, le volcan situé sur l’île de la Réunion a connu une crise éruptive. Cet évènement a été imagé par le satellite radar ALOS dont la longueur d’onde de travail est de 23,6 cm. L’analyse comparée des deux images (Jour 1 et Jour 46) a permis la construction d’un interférogramme.

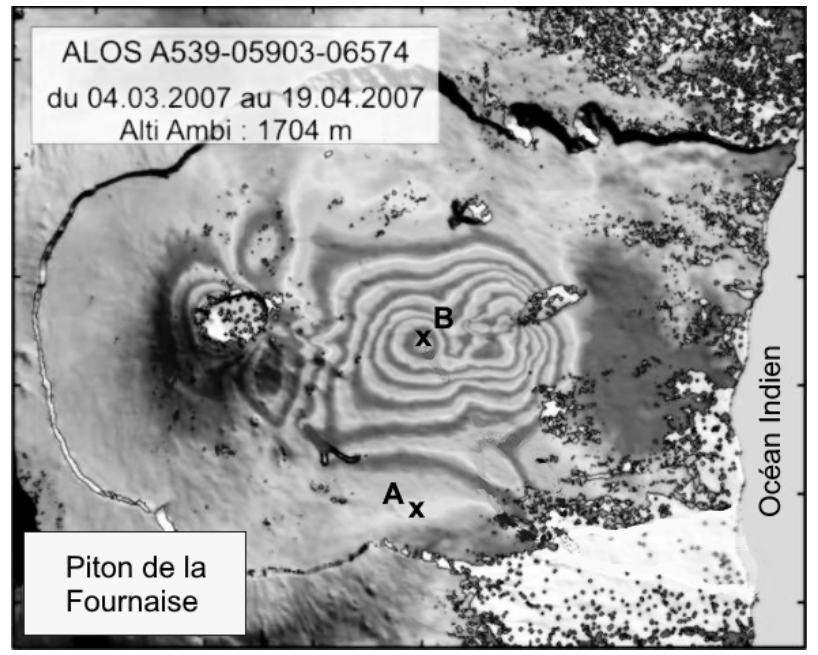
Figure 5 : interférogramme obtenu par superposition des images du 04 mars et du 19 avril 2007

Sur la figure 5, les franges les plus claires correspondent à des interférences constructives.

Q.13. Déterminer l’entier k entre les points A et B et en déduire la variation d’altitude du point B en supposant que le point A n’a pas subi de déplacement.

Entre les points A et B, il y a 6 interférences constructives. Ainsi $k=6$.
Calculons la variation d’altitude du point B en supposant que le point A n’a pas subi de déplacement.

$d=k\times\frac{\lambda}{2}$
$d=6\times\frac{23,6\times{10}^{-2}}{2}$
$d=0,71\ m$
$d=71\ cm$