Utilisation d’un laser comme instrument de mesure

Bac Liban 2024 Sujet 1

Exercice 2 – (6 points) – Durée 1h03 – Calculatrice autorisée

Sujet n°24-PYCJ1G11

EXERCICE 2 : utilisation d’un laser comme instrument de mesure (6 points)

On souhaite savoir si un voile en polyester peut être utilisé comme moustiquaire. Pour ce faire, on mesure la taille des mailles rectangulaires à l’aide d’un montage de laboratoire.

1. Vérification de la longueur d’onde du laser

Le montage ci-dessous est réalisé avec une diapositive comportant une fente de largeur connue.

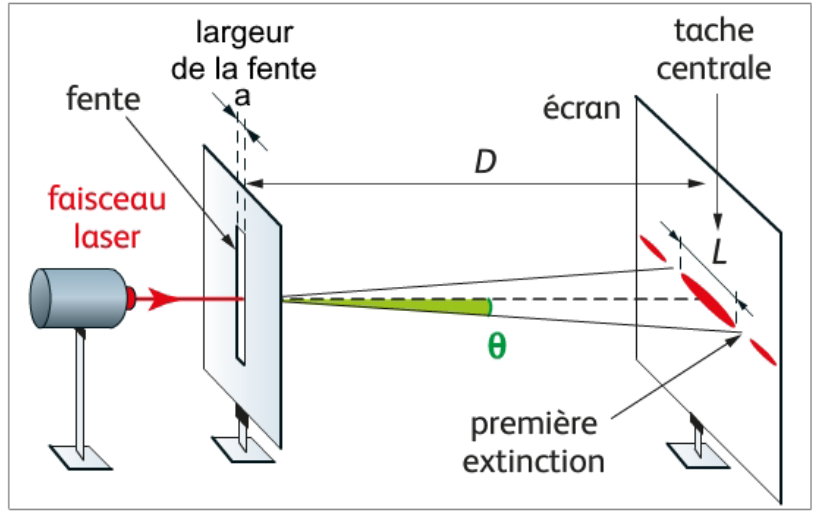
Figure 1 : montage de diffraction

Une série de mesures, avec une distance D = (1800 ± 2) mm est effectuée. Les résultats obtenus sont consignés dans le tableau suivant :

a (µm)	30	40	60	80	100	150	200
L (mm)	77	59	40	30	24	16	12

Données :

approximations des petits angles, exprimés en radians : sin θ ≈ θ et tan θ ≈ θ ;
relation théorique entre l’angle de diffraction q et la valeur de la largeur de la fente a pour les petits angles : $\theta=\frac{\lambda}{a}$ ;
accord d’une mesure avec une valeur de référence : on compare, le cas échéant, le résultat d’une mesure X à une valeur de référence X_réfen utilisant le quotient $\left|\frac{x-x_{ref}}{u(x)}\right|$ où u(X) est l’incertitude-type associée au résultat.

Q.1. Exprimer, à l’aide de la figure 1, l’angle de diffraction θ en fonction de la largeur L de la tache centrale et de la distance D.

Lorsque $\theta$ est petit, on considère que $tan\ \left(\theta\right)\approx\theta$ :
$$tan\ (\theta)\ =\frac{L}{2D}$$
$$\theta\ =\frac{L}{2D}$$

En utilisant un tableur et la relation précédente, on obtient le tableau suivant :

1/a (m^-1)	3,33·10⁴	2,50·10⁴	1,67·10⁴	1,25·10⁴	1,00·10⁴	6,67·10³	5,00·10³
θ(rad)	2,14·10^–²	1,64·10^–²	1,11·10^–²	8,33·10^–³	6,67·10^–³	4,44·10^–³	3,33·10^–³

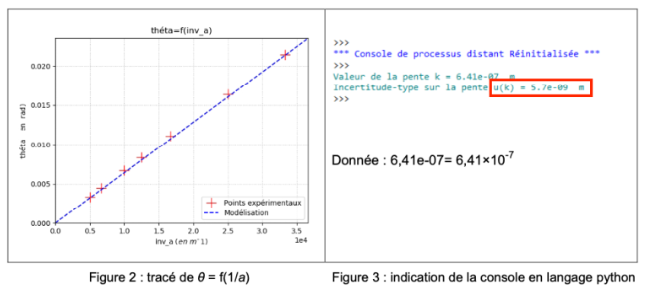
Un script écrit en langage python permet ensuite de tracer θ = f(1/a). On obtient les figures 2 et 3 ci-dessous dans lesquelles θ sera noté théta et 1/a sera noté inv_a :

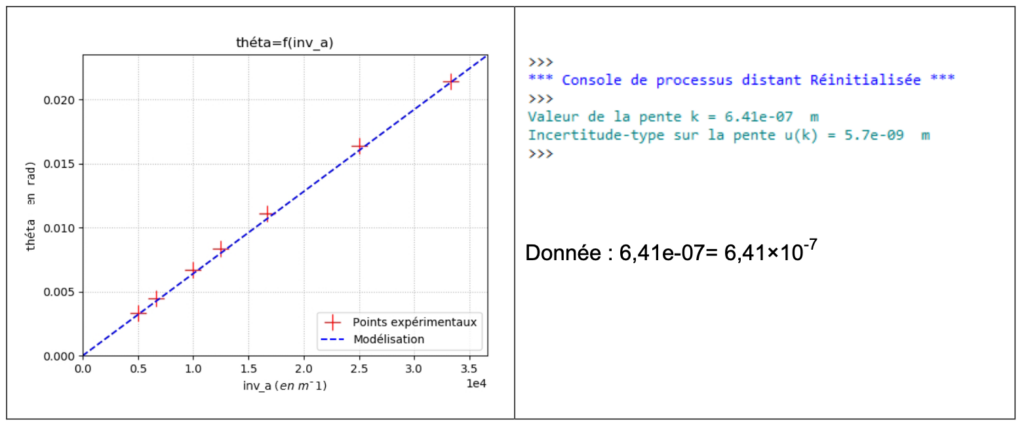
Figure 2 : tracé de θ = f(1/a) Figure 3 : indication de la console en langage python

Q.2. Déduire des informations précédentes la valeur de la longueur d’onde λ_laser du laser utilisé. Justifier.

Le graphique montre une droite passant par l’origine : $\theta$ est proportionnel à $\frac{\mathbf{1}}{\mathbf{a}}$
$$\theta\ =k\times \frac{1}{a}$$
aoverrightarrow $k=6,41\times 10^{-7}\ m$
$$\theta\ =6,41\times 10^{-7}\times \frac{1}{a}$$
$$\theta\ =\frac{6,41\times 10^{-7}}{a}$$

Or
$$\theta=\frac{\lambda}{a}$$
Par identification : $\lambda=6,41\times 10^{-7}\ m$
$\lambda=641\ nm$

Q.3. Indiquer si la valeur mesurée est en accord avec la longueur d’onde λréf = 650 nm indiquée sur la notice fournie par le constructeur.

Calculons le z-score :
$$z=\left|\frac{\lambda_{mesure}-\lambda_{ref}}{u\left(\lambda\right)}\right|$$
$$z=\left|\frac{641\times 10^{-9}-650\times 10^{-9}}{5,7\times 10^{-9}}\right|$$
$$z=1,6$$
$z<2$ : la valeur mesurée est en accord avec la longueur d’onde $\lambda_{réf}=650\ nm$ indiquée sur la notice fournie par le constructeur.

2. Mesure de la taille d’une maille rectangulaire d’un voile polyester

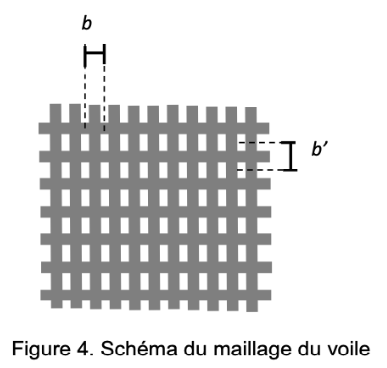
Le but de cette partie est de mesurer les dimensions b et b’ du voile polyester disponible dont le maillage est représenté sur la figure suivante :

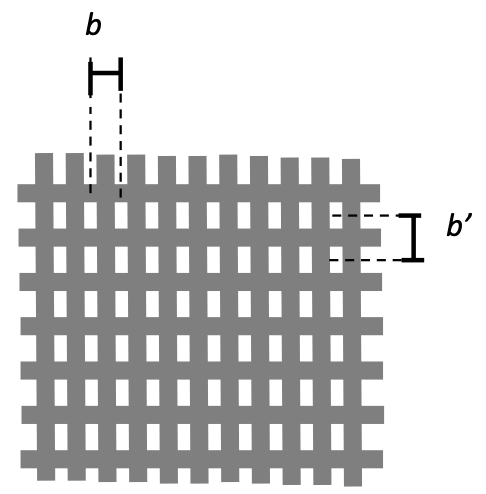
Figure 4. Schéma du maillage du voile

On réalise une expérience d’interférences pour évaluer ces dimensions en utilisant la diode laser précédente et en réalisant le montage suivant :

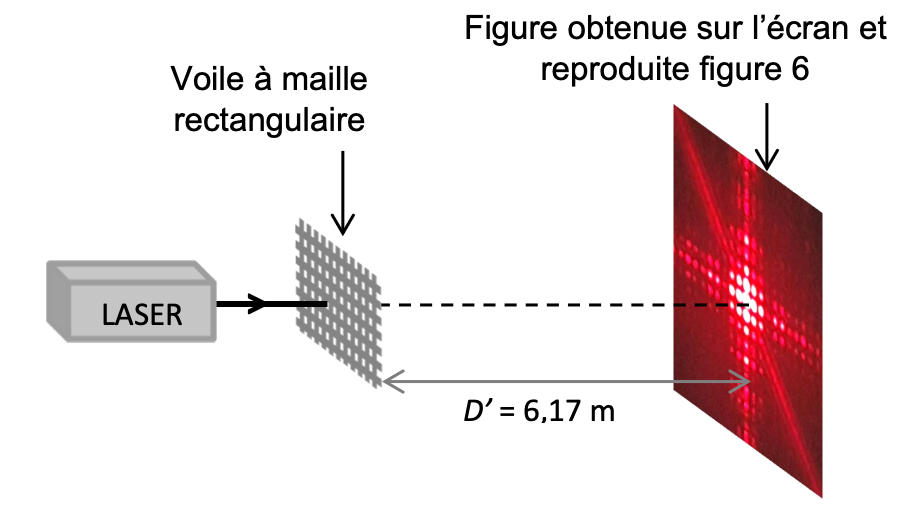
Figure 5. Montage utilisé (échelle non respectée)

Données :

diode laser de longueur d’onde λ = (650 ± 20) nm où ce qui suit le ± représente l’incertitude-type associée à la longueur d’onde ;
distance D’ = (6,17 ± 0,03) m où ce qui suit le ± représente l’incertitude-type associée à la distance ;
on note b la distance entre les centres de deux trous consécutifs du maillage horizontal et b’ la distance entre les centres de deux trous consécutifs du maillage vertical du voile ;
la figure d’interférences obtenue est donnée sur la figure suivante :

Figure 6 : interférences obtenues avec le voile

l’interfrange horizontale, notée i, est définie comme la distance entre les centres de deux taches lumineuses successives selon l’axe horizontal identifié sur la figure 6 ;
l’interfrange verticale, notée i’, est définie comme la distance entre les centres de deux taches lumineuses successives selon l’axe vertical identifié sur la figure 6 ;
L’expression de l’interfrange est donnée par la relation : $i=\frac{\lambda\times D’}{b}$ et $i’=\frac{\lambda\times D’}{b’}$
L’incertitude-type u(b) sur la grandeur b peut se calculer à partir de la relation :

$$\frac{u(b)}{b}=\sqrt{\left(\frac{u(D’)}{D’}\right)^2+\left(\frac{u(i)}{i}\right)^2+\left(\frac{u(\lambda)}{\lambda}\right)^2}$$

où u(x) désigne l’incertitude-type associée à la grandeur x.

Q.4. Évaluer les valeurs des interfranges, i et i’, à l’aide des dimensions figurant sur la figure 6.

L’interfrange horizontale, notée $i$, est définie comme la distance entre les centres de deux taches lumineuses successives selon l’axe horizontal identifié sur la figure 6 ;

$$7i=45\ mm$$
$$i=\frac{45}{7}$$
$$i=6,4\ mm$$

L’interfrange verticale, notée $i\prime$, est définie comme la distance entre les centres de deux taches lumineuses successives selon l’axe vertical identifié sur la figure 6 ;

$$4i\prime=18\ mm$$
$$i\prime=\frac{18}{4}$$
$$i\prime=4,5\ mm$$

Q.5. En déduire les valeurs des dimensions b et b’ du voile utilisé, ainsi que leurs incertitudes associées, en considérant les incertitudes-types sur i et i’ : u(i) = u(i’) = 0,1mm. Écrire les résultats avec un nombre adapté de chiffres significatifs.

$$i=\frac{\lambda\times D\prime}{b}$$
$$i\times b=\lambda\times D\prime$$
$$b=\frac{\lambda\times D\prime}{i}$$
$$b=\frac{650\times 10^{-9}\times 6,17}{6,4\times 10^{-3}}$$
$$b=6,3\times 10^{-4}\ m$$

$$\frac{u(b)}{b}=\sqrt{\left(\frac{u(D\prime)}{D\prime}\right)^2+\left(\frac{u(i)}{i}\right)^2+\left(\frac{u(\lambda)}{\lambda}\right)^2}$$
$$u(b)=b\times \sqrt{\left(\frac{u(D\prime)}{D\prime}\right)^2+\left(\frac{u(i)}{i}\right)^2+\left(\frac{u(\lambda)}{\lambda}\right)^2}$$
$$u(b)=6,3\times 10^{-4}\times \sqrt{\left(\frac{0,03}{6,17}\right)^2+\left(\frac{0,1}{6,4}\right)^2+\left(\frac{20}{650}\right)^2}$$
$$u\left(b\right)=3\times 10^{-5}m$$ valeur arrondi à l’excès.

$$b=6,3\times 10^{-4}\pm 3\times 10^{-5}\ m$$
$$b=\left(6,3\pm 0,3\right)\times 10^{-4}\ m$$

$$i\prime=\frac{\lambda\times D\prime}{b\prime}$$
$$i\prime\times b\prime=\lambda\times D\prime$$
$$b\prime=\frac{\lambda\times D\prime}{i\prime}$$
$$b\prime=\frac{650\times 10^{-9}\times 6,17}{4,5\times 10^{-3}}$$
$$b\prime=8,9\times 10^{-4}\ m$$

$$\frac{u(b\prime)}{b\prime}=\sqrt{\left(\frac{u(D\prime)}{D\prime}\right)^2+\left(\frac{u(i\prime)}{i\prime}\right)^2+\left(\frac{u(\lambda)}{\lambda}\right)^2}$$
$$u(b\prime)=b\prime\times \sqrt{\left(\frac{u(D\prime)}{D\prime}\right)^2+\left(\frac{u(i)}{i}\right)^2+\left(\frac{u(\lambda)}{\lambda}\right)^2}$$
$$u(b\prime)=8,9\times 10^{-4}\times \sqrt{\left(\frac{0,03}{6,17}\right)^2+\left(\frac{0,1}{4,5}\right)^2+\left(\frac{20}{650}\right)^2}$$
$$u\left(b\prime\right)=4\times 10^{-5}m$$ valeur arrondi à l’excès.

$$b\prime=8,9\times 10^{-4}\pm 4\times 10^{-5}\ m$$
$$b\prime=\left(8,9\pm 0,4\right)\times 10^{-4}\ m$$

Q.6. Expliquer pourquoi la distance D utilisée dans le montage de la partie 1 a dû être remplacée par une distance D’ pour effectuer la mesure de la partie 2.

$D=1800\ mm$
$D=1,800\ m$

$D’=6,17\ m$

$D’>D$.

L’interfrange $i$ est proportionnelle à $D$ :
$$i=\frac{\lambda\times D}{b}$$
Ainsi, pour obtenir une interfrange plus grande, donc plus facilement mesurable, la distance $D$ utilisée dans le montage de la partie 1 a dû être remplacée par une distance $D’$.

Selon les recommandations de l’ECARF (fondation européenne de recherche sur les allergies), une moustiquaire anti-pollen doit posséder à minima 3 fois plus d’ouvertures par cm² qu’une moustiquaire classique qui en comporte 50 par cm².

Q.7. Estimer le nombre d’ouvertures par cm² du voile polyester testé. Indiquer s’il est utilisable comme moustiquaire anti-pollen selon l’ECARF.

Le candidat est invité à prendre des initiatives et à présenter sa démarche. Toute démarche pertinente, même non aboutie, sera valorisée.

Estimons le nombre d’ouvertures par cm² du voile polyester testé.

Nombre d’espaces horizontale	Dimensions
1	$6,3\times 10^{-4}\ m$
N	$1,0\ cm\ =\ 1,0\times 10^{-2}\ m$

$$N=\frac{1,0\times 10^{-2}\times 1}{6,3\times 10^{-4}}$$
$$N=16$$

Nombre d’espaces verticale	Dimensions
1	$8,9\times 10^{-4}\ m$
N’	$1,0\ cm\ =\ 1,0\times 10^{-2}\ m$

$$N\prime=\frac{1,0\times 10^{-2}\times 1}{8,9\times 10^{-4}}$$
$$N\prime=11$$

Nombre d’ouvertures par cm²
$Nombre\ d\prime ouvertures=N\times N\prime$
$Nombre\ d\prime ouvertures=16\times 11$
$Nombre\ d\prime ouvertures=176\ par\ {cm}^2$

Une moustiquaire classique en comporte 50 par cm².
Salon les recommandations de l’ECARF (fondation européenne de recherche sur les allergies), une moustiquaire anti-pollen doit posséder à minima 3 fois plus d’ouvertures par cm².
Pour en comporter 3 fois plus il en faut : $50\times 3\ =150\ ouvertures\ par\ {cm}^2$

Le voile polyester testé comporte 3 fois plus d’ouvertures par cm² qu’une moustiquaire classique.
Ainsi, le voile polyester testé est utilisable comme moustiquaire anti-pollen selon l’ECARF.