Couverture de survie ou couverture de laine

Bac Liban 2024 Sujet 2

Exercice 3 – (5 points) –  Durée 0h53 – Calculatrice autorisée

Sujet n°24-PYCJ2G11

EXERCICE 3 : couverture de survie ou couverture en laine ? (5 points)

Photo : Filippo Bacci Istock

Les couvertures de survie actuelles sont revêtues de deux faces métallisées distinctes, respectivement dorée et argentée, qui enveloppent une couche de PET (Polyéthylène téréphtalate) qui isole de l’humidité ambiante ou à l’inverse évite la déshydratation. Les deux faces répondent à deux fonctions distinctes : le côté argenté, initialement développé par la Nasa, réfléchit 90 % du rayonnement infrarouge, tandis que le côté doré absorbe 50 % de l’énergie thermique incidente. De ce fait, si on positionne la face dorée vers l’extérieur, on protège la personne de l’humidité et du froid, en retenant sa chaleur corporelle. Si à l’inverse, on la place côté intérieur, on le protège du coup de chaud.

D’après Sciences et Avenir.

Q.1. Citer les trois modes de transferts thermiques. Préciser celui pour lequel il est majoritairement nécessaire de protéger les satellites.

Les trois modes de transfert thermiques sont :
• La conduction
• La convection
• Le rayonnement

Le rayonnement est le mode de transfert duquel il faut protéger les satellites.

Une personne est recouverte d’une couverture. Dans cette partie, on étudie le transfert thermique par conduction à travers la couverture.

Le coefficient de transfert thermique de conduction, noté u en W·K^-1·m^-2, indique la facilité avec laquelle l’énergie thermique est transférée d’un milieu à un autre à travers une paroi. Des mesures ont été réalisées avec une couverture de survie d’épaisseur e₁ = 38 µm et avec une couverture en laine d’épaisseur e₂ = 0,50 mm.

Les valeurs obtenues sont u₁ = 408 W·K^-1·m^-2 pour la couverture de survie et u₂ = 38 W·K^-1·m^-2 pour la couverture en laine.

La conductivité thermique d’un matériau représente sa capacité à permettre le transfert thermique par conduction, elle se note l et s’exprime en W·K^-1·m^-1.

Q.2. Établir, en s’appuyant sur une analyse dimensionnelle, la relation entre u, l et e.

L’unité de u ressemble à celle de $\lambda$. Cependant u est en W.K$^{-1}$.m$^{-2}$ alors que $\lambda$ est en W.K$^{-1}$.m$^{-1}$. Pour passer de l’un à l’autre il faut multiplier (ou diviser) par une grandeur en mètre m :
$u=\frac{\lambda}{e}$

Q.3. Calculer la valeur de la conductivité thermique de la couverture de survie et celle de la couverture en laine. Les comparer puis commenter.

$u=\frac{\lambda}{e}$
$\frac{\lambda}{e}=u$
$\lambda=u\times e$

Pour la couverture de survie :
$\lambda_{couverture\ de\ survie}=u_{couverture\ de\ survie}\times e_{couverture\ de\ survie}$
$\lambda_{couverture\ de\ survie}=u_1\times e_1$
$\lambda_{couverture\ de\ survie}=408\times38\times{10}^{-6}$
$\lambda_{couverture\ de\ survie}=1,6\times{10}^{-2}\ W.K^{-1}.m^{-1}$

Pour la couverture en laine :
$\lambda_{couverture\ en\ laine\ }=u_{couverture\ en\ laine\ }\times e_{couverture\ en\ laine\ }$
$\lambda_{couverture\ en\ laine\ }=u_2\times e_2$
$\lambda_{couverture\ en\ laine\ }=38\times0,50\times{10}^{-3}$
$\lambda_{couverture\ en\ laine\ }=1,9\times{10}^{-2}\ W.K^{-1}.m^{-1}$

$\lambda_{couverture\ en\ laine\ }>\lambda_{couverture\ de\ survie}$ : la couverture en laine est moins isolante que la couverture de survie.

Le rayonnement du corps humain se fait essentiellement dans l’infrarouge.

On réalise au laboratoire une expérience avec une lampe à halogène dont le spectre est donné figure 1. La radiance est proportionnelle à la puissance du rayonnement par unité de surface.

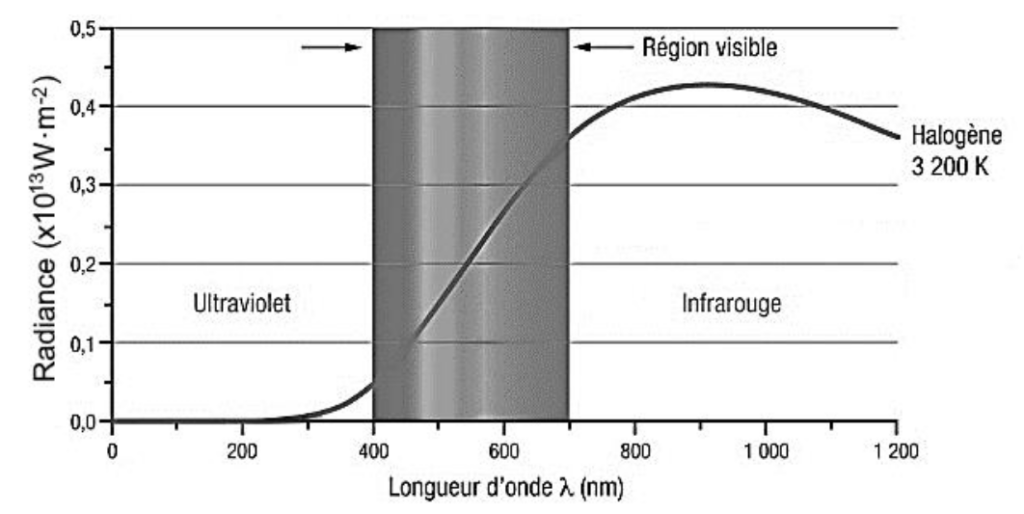
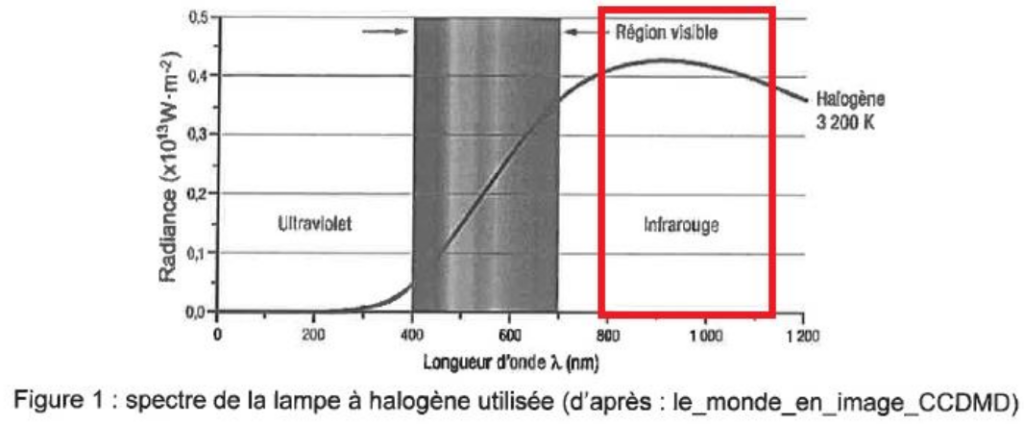
Figure 1 : spectre de la lampe à halogène utilisée (d’après : le_monde_en_image_CCDMD)

Q.4. Indiquer le domaine d’onde dans lequel la lampe à halogène émet le plus de rayonnement et justifier son utilisation pour l’étude du transfert thermique à travers les couvertures.

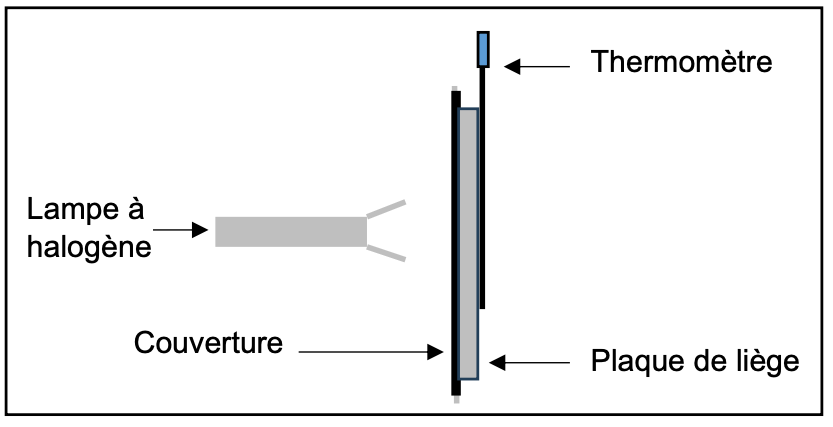
Figure 2 : schéma du dispositif expérimental

Données :

• épaisseur de la plaque de liège : 1,0 cm ;
• masse de la plaque de liège : 72,4 g ;
• capacité thermique massique du liège : cliege = 2008 J·K^-1·kg^-1 .

On obtient les courbes, figures 3 et 4, qui donnent l’évolution de la température du liège en fonction du temps.

On modélise la partie rectiligne de chaque courbe, correspondant à un flux constant, pour déterminer le coefficient directeur $\frac{\Delta T}{\Delta t}$ en °C·s^-1.

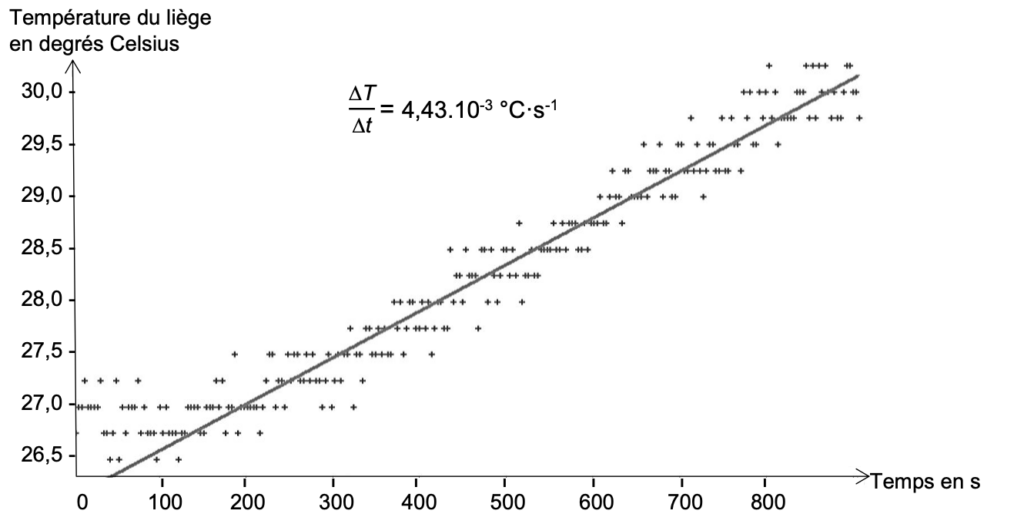
Figure 3 : évolution de la température du liège en fonction du temps, dans l’étude de la couverture de survie.

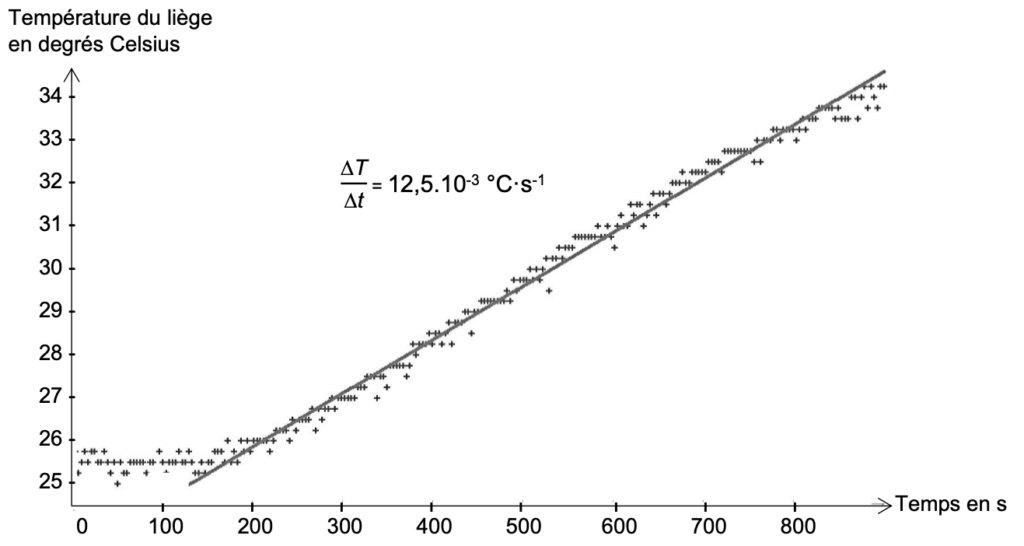
Figure 4 : évolution de la température du liège en fonction du temps, dans l’étude de la couverture en laine.

Q.5. Montrer que l’expression de la variation d’énergie interne d’un système incompressible peut s’exprimer : ΔU = m·c·ΔT (m : masse du système ; c : capacité thermique massique du système ; ΔT : variation de température du système).

Premier principe de la thermodynamique :
$\Delta U=Q+W$
Ici $W=0$
$\Delta U=Q$
$\Delta U=m\times c\times\Delta T$

Q.6. Exprimer le flux thermique Φ à travers la plaque de liège en fonction de la variation de température et du temps.

$\phi=\frac{Q}{\Delta t}$
$\phi=\frac{m\times c\times\Delta T}{\Delta t}$

Pour chaque expérience en régime permanent, on suppose que le flux thermique qui traverse la couverture est le même que celui qui traverse la plaque de liège.

Q.7. Comparer l’efficacité des deux couvertures à retenir la chaleur corporelle.

On considère que le flux thermique qui traverse la couverture est le même que celui qui traverse la plaque de liège :
$\phi_{couverture\ de\ survie}=\phi_{liege}$
$\phi_{couverture\ de\ survie}=\frac{m\times c_{liege}\times\Delta T}{\Delta t}$
$\phi_{couverture\ de\ survie}=72,4\times{10}^{-3}\times2008\times4,43\times{10}^{-3}$
$\phi_{couverture\ de\ survie}=0,64\ W$

$\phi_{couverture\ en\ laine}=\phi_{liege}$
$\phi_{couverture\ en\ laine}=\frac{m\times c_{liege}\times\Delta T}{\Delta t}$
$\phi_{couverture\ en\ laine}=72,4\times{10}^{-3}\times2008\times12,5\times{10}^{-3}$
$\phi_{couverture\ en\ laine}=1,82\ W$

Ainsi : $\phi_{couverture\ de\ survie}<\phi_{couverture\ en\ laine}$

Le flux thermique de la couverture de survie est plus petit que le flux thermique de la couverture en laine.

Plus le flux est petit, moins il y a de transferts thermiques, meilleure est l’isolation.

Ainsi, la couverture de survie est plus efficace que la couverture en laine pour retenir la chaleur corporelle