Bac Polynésie 2024 Sujet 1
Exercice 3 – (6 points) – Durée 1h03 – Calculatrice autorisée
Sujet n°24-PYCJ1PO1
Sujet et corrigé
EXERCICE 3 – UNE JEUNE ASTRONOME (6 POINTS)
Une élève de terminale est intéressée par l’astronomie. Elle rêve de pouvoir observer le ciel par ses propres moyens. Pour cela, elle souhaite s’acheter une lunette astronomique qui lui permettra d’observer la Lune, le Soleil (par projection, car il ne faut jamais l’observer directement) et les planètes du Système solaire.
Elle a un budget limité et ne pourra s’offrir qu’une lunette premier prix. Ayant étudié les principes de la lunette astronomique, elle souhaite vérifier à l’aide de ses connaissances si cette lunette lui permettra d’observer la grande tache rouge de Jupiter.
Le but de l’exercice est de procéder à cette vérification et de déterminer si la grande tache rouge sera visible même au plus faible grossissement.
Vérification des caractéristiques commerciales de la lunette.
Dans un premier temps, cette élève veut vérifier que les grossissements de ×30 et ×150 annoncés par le fabricant sont corrects.
Données :
- Extrait de la notice de la lunette astronomique :
- Caractéristiques commerciales de la lunette à objectif achromatique :
- Diamètre de l’objectif D = 50 mm
- Distance focale f’1 = 60,0 cm
- Grossissement avec accessoires compris : ×30 et ×150
- Masse nette : 1 kg
- Eléments livrés :
- Lunette et monture
- Trépied en aluminium réglable en hauteur
- Deux oculaires de distances focales f’2 = 4 mm et f’2 = 20 mm
- Filtre lunaire
- Caractéristiques commerciales de la lunette à objectif achromatique :
- On rappelle que pour les petits angles θ : tan θ ≈ θ et sin θ ≈ θ.
Q1. La lunette astronomique est un système optique afocal. Donner la signification du terme afocal.
Un système optique est dit afocal s’il donne d’un objet à l’infini une image à l’infini.
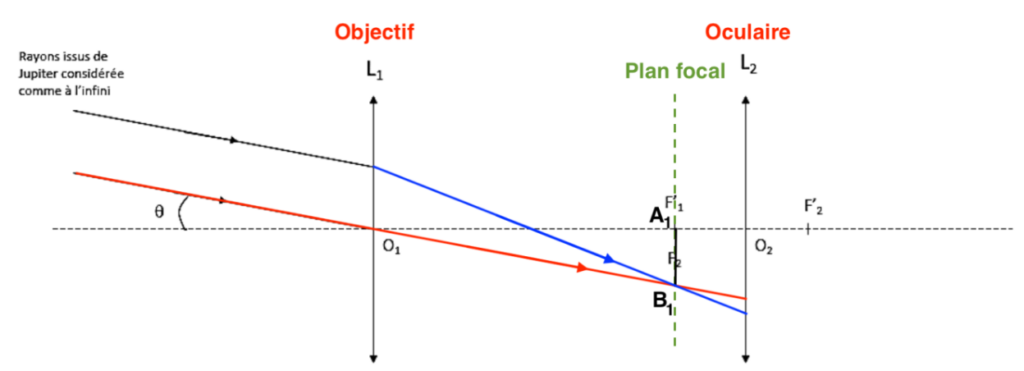
Q2. Placer les termes objectif et oculaire sur le schéma du document réponse.
L1 : l’objectif car c’est une lentille convergente possédant une grande distance focale. C’est la lentille placée vers l’objet.
L2 : l’oculaire car c’est une lentille convergente possédant une petite distance focale. C’est la lentille où on place l’œil.
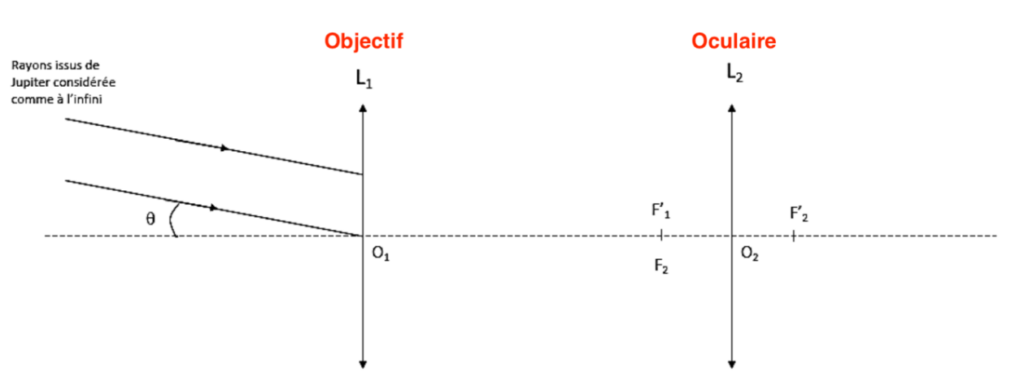
Q3. Tracer, sur le schéma du document réponse, le trajet des rayons arrivant de Jupiter considéré comme situé à l’infini en faisant figurer les traits de construction.
Le rayon lumineux issu de B pénétrant dans la lunette par le centre optique O1 de la lentille L1 n’est pas dévié.
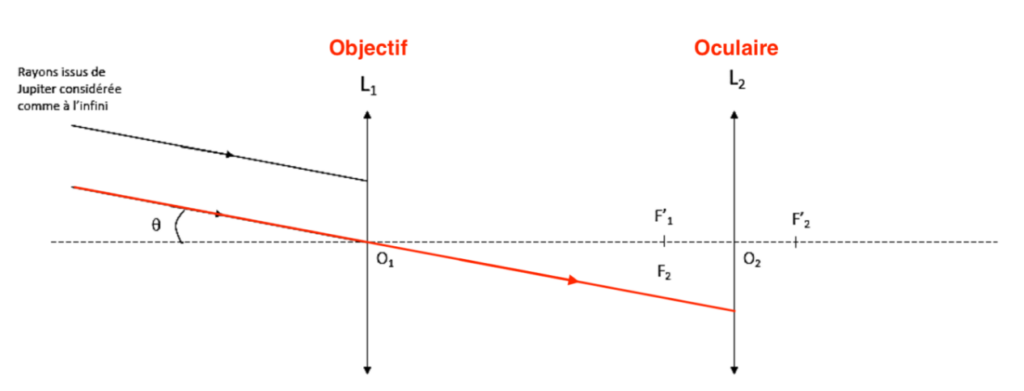
Position de B1 image intermédiaire de B : Comme l’objet A∞B∞ est à l’infini, son image A1B1 est dans le plan focal image de l’objectif L1.
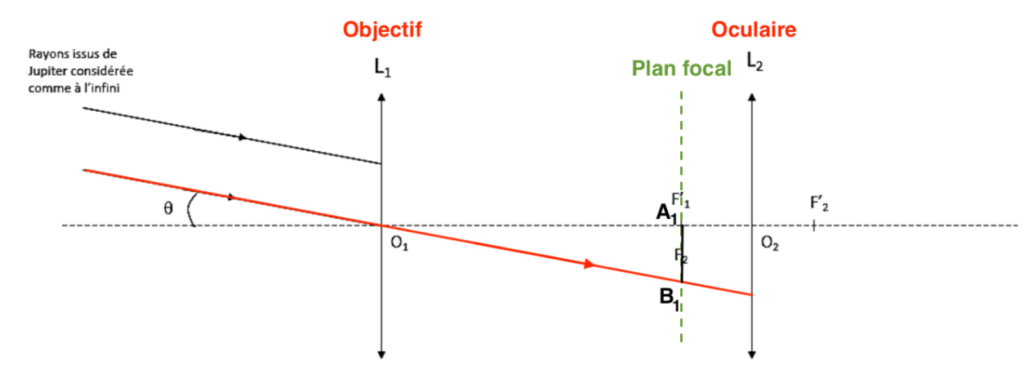
L’autre rayon lumineux issus de B, sort de L1 en passant par B1.
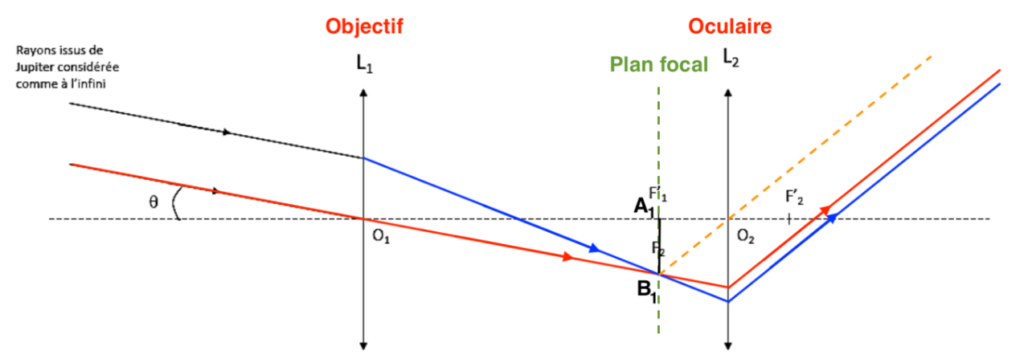
Pour le rayon émergeant de la lentille L2 :
- On trace un rayon issu de B1 passant par O2. Ce rayon ne sera pas dévié.
- De plus nous savons que l’image d’un objet situé dans le plan focal objet d’une lentille se forme à l’infini. Ainsi les rayons émergeants de la lentille L2 issue de B1 seront parallèles à ce rayon tracé.
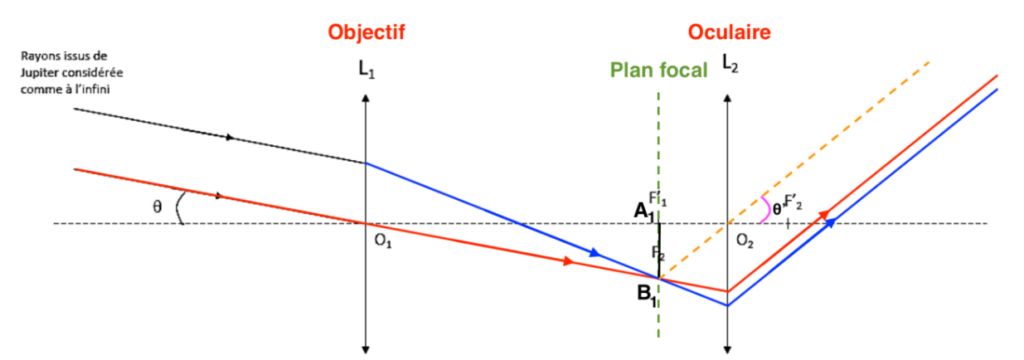
Q4. Placer, sur le schéma du document réponse, l’angle apparent θ’ de l’objet à travers la lunette.
Q5. Donner la définition du grossissement G de la lunette. Montrer que l’expression du grossissement est $G=\frac{f_1}{f_2}$ et vérifier que les grossissements annoncés par le fabricant sont corrects.
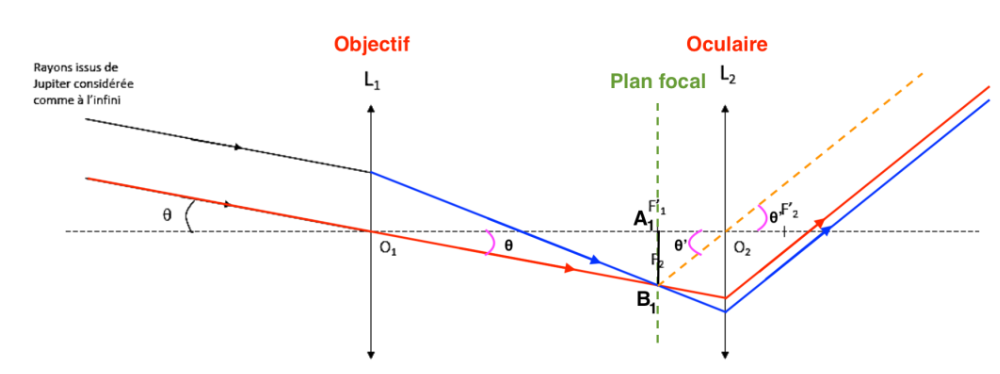
Le grossissement G d’une lunette astronomique est défini par :
$$G=\frac{\theta^\prime}{\theta}$$
$$\tan\left(\theta\right)\approx \theta=\frac{A_1B_1}{f_1^\prime}$$
$$\tan\left(\theta^\prime\right)\approx \theta^\prime=\frac{A_1B_1}{f_2^\prime}$$
$$G=\frac{\theta^\prime}{\theta}=\frac{\frac{A_1B_1}{f_2^\prime}}{\frac{A_1B_1}{f_1^\prime}}=\frac{A_1B_1}{f_2^\prime}\times \frac{f_1^\prime}{A_1B_1}=\frac{f_1^\prime}{f_2^\prime}$$
Vérifions que les grossissements annoncés par le fabricant sont corrects :
Avec l’oculaire de distances focales f’2 = 4 mm
$$G=\frac{f_1^\prime}{f_2^\prime}$$
$$G=\frac{60,0\times {10}^{-2}}{4\times {10}^{-3}}$$
$$G=150$$
Avec l’oculaire de distances focales f’2 = 20 mm
$$G=\frac{f_1^\prime}{f_2^\prime}$$
$$G=\frac{60,0\times {10}^{-2}}{20\times {10}^{-3}}$$
$$G=30$$
Ainsi, les grossissements annoncés par le fabricant ($\times 30$ et $\times 150$) sont corrects.
Visibilité de la grande tache rouge de Jupiter.
La planète Jupiter est une planète gazeuse qui présente à sa surface un système de bandes de nuages clairs et sombres, mais surtout une grande tache rouge, un ouragan gigantesque qui souffle depuis au moins cinq siècles, date de sa première observation.

Figure 1. Jupiter et la grande tache rouge.
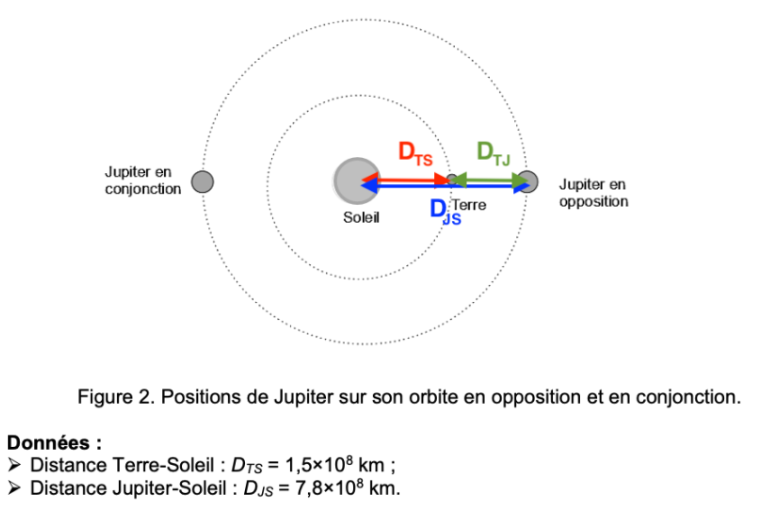
Jupiter peut être en conjonction ou en opposition avec la Terre. Jupiter est en opposition quand elle est située sur son orbite du même côté du Soleil que la Terre. Jupiter est en conjonction quand elle est située de l’autre côté de son orbite. Les positions de Jupiter en opposition et en conjonction sont représentées sur la figure 2.
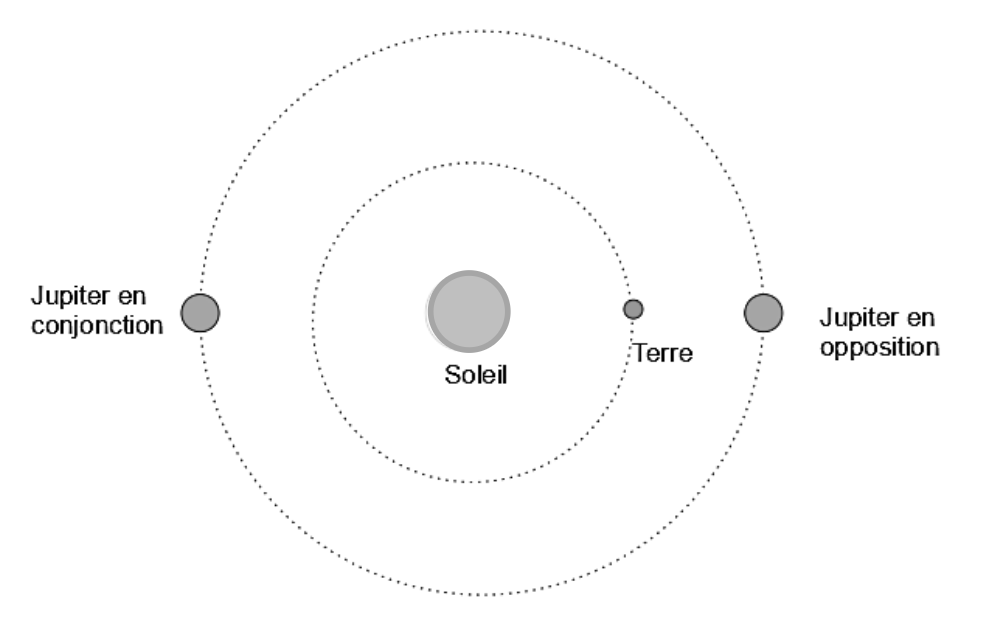
Figure 2. Positions de Jupiter sur son orbite en opposition et en conjonction.
Données :
- Distance Terre-Soleil : DTS = 1,5×108 km ;
- Distance Jupiter-Soleil : DJS = 7,8×108 km.
Q6. Indiquer la meilleure situation pour observer Jupiter. Calculer alors la valeur de la distance Terre-Jupiter DTJ.
La meilleure situation pour observer Jupiter est la position dans laquelle Jupiter est la plus proche : quand elle est en opposition.
$$D_{TJ}=D_{JS}-D_{TS}$$
$$D_{TJ}=7,8\times {10}^8-1,5\times {10}^8$$
$$D_{TJ}=6,3\times {10}^8\ km$$
Donnée :
- La grande tache rouge est devenue quasiment circulaire avec un diamètre D = 1,5×104 km.
Le schéma de la figure 3 représente l’angle apparent θ de la grande tache rouge de Jupiter.
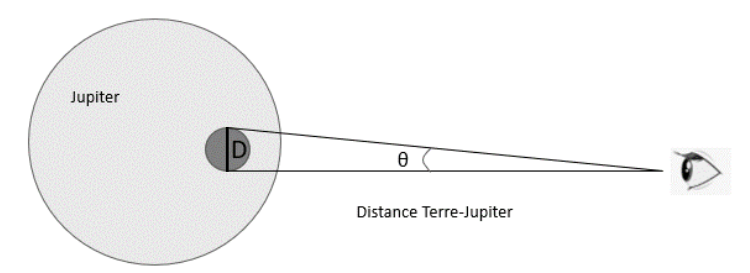
Figure 3. Schéma représentant l’angle apparent de la grande tache rouge.
Q7. Calculer le diamètre apparent θ de la grande tache rouge vue à l’œil nu.
Calculons le diamètre apparent θ de la grande tache rouge vue à l’œil nu.
Pour des angles très petits, exprimés en radian : tan θ ≈ θ
$$\theta\approx \tan\ \theta=\frac{oppos\acute{e}}{adjacent}$$
$$\theta=\frac{D}{D_{TJ}}$$
$$\theta=\frac{1,5\times {10}^4}{6,3\times {10}^8}$$
$$\theta=2,4\times {10}^{-5}\ rad$$
Q8. Calculer la valeur du diamètre apparent θ’ de la grande tache rouge vue à travers la lunette avec le plus petit grossissement de la lunette.
Calculons la valeur du diamètre apparent θ’ de la grande tache rouge vue à travers la lunette avec le plus petit grossissement de la lunette.
$$G=\frac{\theta^\prime}{\theta}$$
$$\frac{\theta^\prime}{\theta}=G$$
$$\theta^\prime=G\times \theta$$
$$\theta^\prime=30\times 2,4\times {10}^{-5}$$
$$\theta^\prime=7,2\times {10}^{-4}\ rad$$
Un œil humain ne peut pas distinguer deux points si l’angle apparent θ’ entre les deux points est inférieur à 2,9×10–4 rad.
Q9. Déterminer si l’élève pourra voir la grande tache rouge avec cette lunette au plus petit grossissement.
Un œil humain ne peut pas distinguer deux points si l’angle apparent θ’ entre les deux points est inférieur à 2,9×10–4 rad.
$$\theta^\prime=7,2\times {10}^{-4}>2,9\times {10}^{-4}\ rad$$ : l’élève pourra voir la grande tache rouge avec cette lunette au plus petit grossissement.
Q10. Citer un phénomène optique susceptible de dégrader la visibilité de la grande tache rouge.
La diffraction est un phénomène optique susceptible de dégrader la visibilité de la grande tache rouge.
DOCUMENT RÉPONSE À RENDRE AVEC LA COPIE EXERCICE 3 – UNE JEUNE ASTRONOME.
Q2, Q3 et Q4