Enseignement scientifique première
Durée 1h – 10 points – Thème « La Terre, un astre singulier »
[latexpage]
Dès l’Antiquité, les Grecs savaient que la Terre était sphérique. Ils ont même mesuré sa circonférence. Cet exercice étudie deux approches historiques liées à la connaissance de la forme de la Terre.
Partie A. La Terre est ronde
Voici un texte d’après Aristote, philosophe et savant grec (384-322 avant JC), dont la pensée a longtemps influencé les sciences.
Document 1.
« Dans les éclipses de Lune, la ligne qui limite l’ombre est toujours une ligne incurvée. Puisque l’éclipse est due à l’interposition de la Terre entre la Lune et le Soleil, c’est la forme de la surface de la Terre, sphérique, qui produit cette ligne courbe. De plus, la manière dont les astres nous apparaissent ne prouve pas seulement que la Terre est ronde, mais aussi que son étendue est assez petite.
En effectuant un déplacement minime vers le Sud ou vers le Nord, nous voyons se modifier le cercle d’horizon; les astres au-dessus de nous changent considérablement et ce ne sont pas les mêmes qui brillent dans le ciel quand on va vers le Nord et quand on va vers le Sud. Certains astres visibles en Égypte ou vers Chypre sont invisibles dans les régions septentrionales. Par ailleurs les astres qui, dans les régions septentrionales, sont visibles à tout instant, connaissent un coucher dans les pays cités plus haut. Tout cela ne montre pas seulement que la Terre est ronde, mais encore qu’elle a la forme d’une sphère de modeste dimension ; autrement, on n’apercevrait pas si vite les effets d’un déplacement si court. »
Du Ciel, Il, 14, Éd. des Belles Lettres, 1965

Le dessin ci-dessus, qui illustre la démonstration d’Aristote, est extrait de la Cosmographie de Petrus Apianus (1581).
1- Extraire du texte deux observations qui permettent à Aristote d’affirmer que la Terre est ronde.
Deux observations extraits du texte qui permettent à Aristote d’affirmer que la Terre est ronde :
- Dans les éclipses de Lune, la ligne qui limite l’ombre est toujours une ligne incurvée.
- Les astres au-dessus de nous changent considérablement et ce ne sont pas les mêmes qui brillent dans le ciel quand on va vers le Nord et quand on va vers le Sud
2- Donner un autre argument qui permet aujourd’hui de dire que la Terre n’est pas plate.
Le soleil ne se lève pas à la même heure dans les régions du monde : sur une terre plate, ce phénomène ne pourrait pas être observé.
Lorsqu’on voyage et qu’on appel un ami, il fait jour dans notre région et nuit dans la sienne.
3- Citer un objet, autre que la sphère, susceptible de projeter une ombre circulaire.
Un disque est un objet susceptible de projeter une ombre circulaire.
Partie B. Mesure de la circonférence de la Terre
Document 2.
Ératosthène (276 – 194 av JC) est célèbre pour sa méthode de mesure de la circonférence de la Terre. Il était connu qu’à Syène (Assouan aujourd’hui), le 21 juin à midi, on pouvait voir l’image du Soleil se refléter au fond d’un puits. Cela signifie que le Soleil est exactement à la verticale du puits le jour du solstice d’été, c’est-à-dire que Syène est sur le tropique du Cancer. Mais le même jour, à la même heure, dans la ville d’Alexandrie située plus au Nord on constate que les rayons du soleil n’atteignent pas le fond des puits. On mesure que les rayons du Soleil font, avec la verticale, un angle d’un cinquantième de tour (soit 7,2°) comme noté dans le schéma ci-dessous.
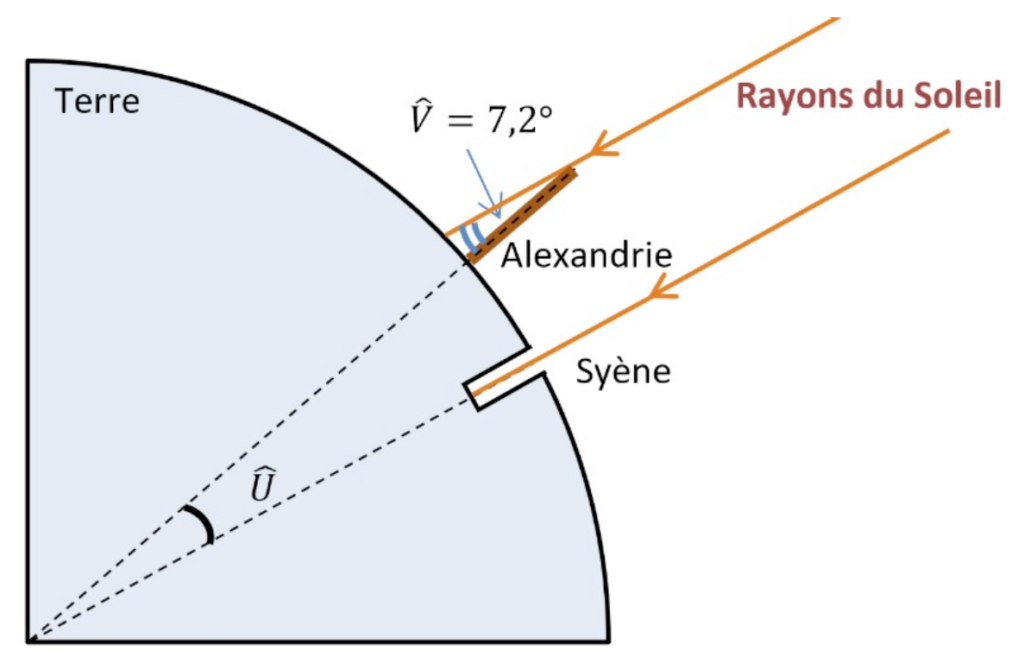
Pour mener son calcul, Ératosthène s’appuie sur plusieurs hypothèses :
- la Terre est sphérique,
- Syène est sur le tropique du Cancer,
- Syène et Alexandrie sont sur le même méridien,
- il faut 50 jours à une caravane de chameaux (qui parcourait une distance quotidienne de 100 stades) pour relier Syène et Alexandrie.
- les rayons du Soleil arrivant sur la Terre sont parallèles entre eux.
Précision : le stade utilisé par Ératosthène est une ancienne unité de longueur valant environ 157 m.
4- En tenant compte de ces hypothèses, déterminer la mesure de l’angle Û au centre de la Terre. Justifier.
Les rayons du soleil sont parallèles entre eux. La droite partant du centre de la Terre vers Alexandrie coupe ces deux droites parallèles. Les angles V ̂ et U ̂ sont alternes internent et sont donc de même valeur. U ̂=V ̂=7,2°
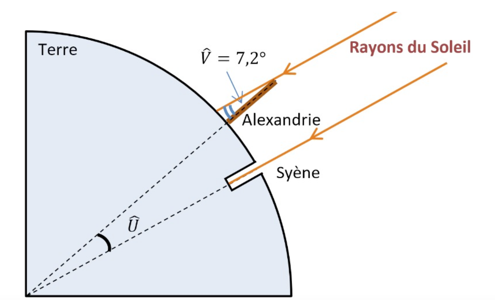
5-a- Déterminer la distance, en kilomètre, entre Syène et Alexandrie.
D’après l’énonce : Il faut 50 jours à une caravane de chameaux (qui parcourait une distance quotidienne de 100 stades) pour relier Syène et Alexandrie.
| 1 stade | 157 m |
| 5 000 stades |
d=(5 000×157)/1
d=785 000 m
d=785 km La distance entre Syène et Alexandrie est 785 km.
5-b- En refaisant les calculs d’Ératosthène, vérifier que son estimation de la circonférence de la Terre est proche de la véritable circonférence de 40 000 km.
Calculons la circonférence de la Terre :
| d=785 km | 7,2° |
| circonférence | 360° |
circonférence=(360×785)/7,2
circonférence=39 250 km
En refaisant les calculs d’Ératosthène on trouve que la circonférence de la Terre est 39 250 km. Son estimation de la circonférence de la Terre est proche de la véritable circonférence de 40 000 km.
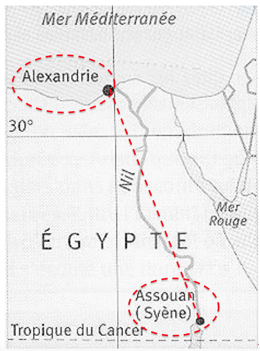
Document 3. Carte actuelle de l’Égypte
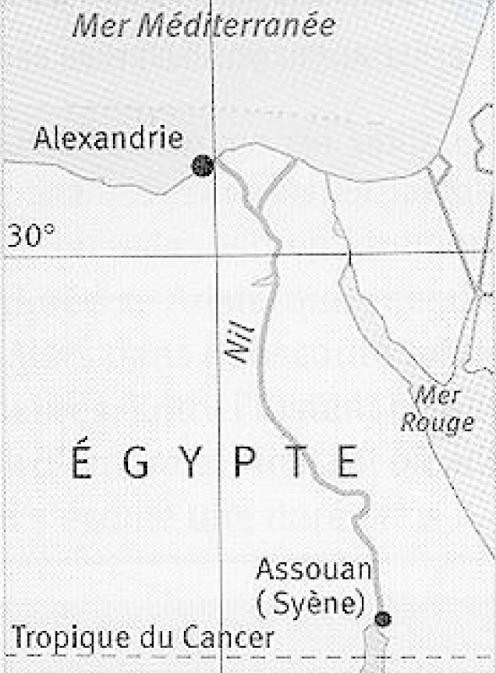
6- En vous aidant de la carte du document 3, quelles hypothèses d’Ératosthène peuvent pourtant être remises en question ?
Hypothèses d’Ératosthène peuvent pourtant être remises en question :
- Syène (Assouan aujourd’hui) est sur le tropique du Cancer. Sur la carte Syène n’est pas exactement sur le tropique du Cancer.
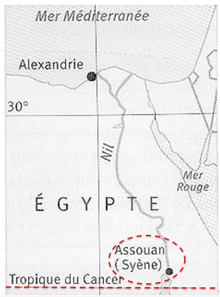
- Syène (Assouan aujourd’hui) et Alexandrie sont sur le même méridien. Sur la carte Syène et Alexandrie ne sont pas exactement sur le même méridien.
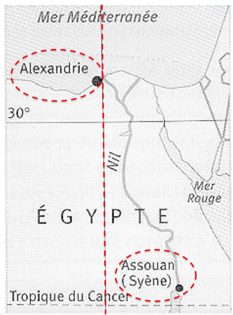
- il faut 50 jours à une caravane de chameaux (qui parcourait une distance quotidienne de 100 stades) pour relier Syène et Alexandrie. sur la carte, nous remarquons qu’un chemin en ligne droite n’est pas possible pour des chameaux car elle coupe le Nil. Ainsi son estimation de la distance entre Syène (Assouan aujourd’hui) et Alexandrie peut être remise en question.