Le street – une pratique olympique

Bac Amérique du nord 2023 Sujet 1

Exercice 1 – (11 points) –  Durée 1h56 – Calculatrice autorisée

Sujet n°23-PYCJ1AN1

EXERCICE 1 : LE STREET – UNE PRATIQUE OLYMPIQUE (11 POINTS)

Image : © Paris 2024

On se propose dans cet exercice d’étudier quelques phases de mouvement simple réalisées par un skateboardeur lors de la pratique du street. Dans tout cet exercice, on appellera skateboardeur le système {skateboard + skateboardeur}. Ce système de masse m est indéformable et modélisé par un point matériel assimilé à son centre de masse G. Les études des différentes phases du mouvement sont effectuées dans le référentiel terrestre considéré galiléen. L’ensemble des phases étudiées est représenté ci-dessous sans souci d’échelle.

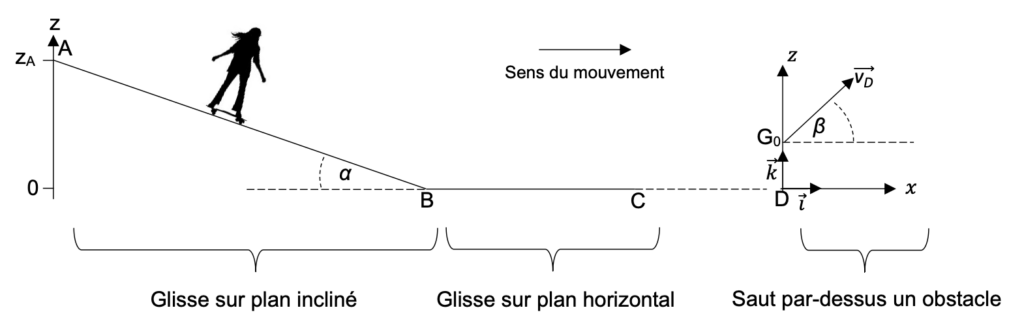
Figure 1. Les différentes phases du mouvement

Données :

• masse du système {skateboardeur + skateboard} : m = 75,0 kg ;
• intensité du champ de pesanteur : g = 9,81 m·s^-2.

A. Glisse sur plan incliné

Le skateboardeur est à l’arrêt au point A en haut d’un module de plan incliné de longueur AB faisant un angle α avec le plan l’horizontal. Le skateboardeur s’élance sans vitesse initiale le long de la pente pour rejoindre le point B. Durant cette phase, on considère que les frottements de l’air sont négligeables et que les frottements des roues sur la piste sont modélisés par une force notée $\overrightarrow{F}$.

Le script en langage de programmation Python ci-dessous permet de tracer les courbes représentatives des énergies du système en fonction du temps, le long du trajet AB.

Script en langage de programmation Python :

1	import matplotlib.pyplot as plt
2
3	#Saisie des valeurs
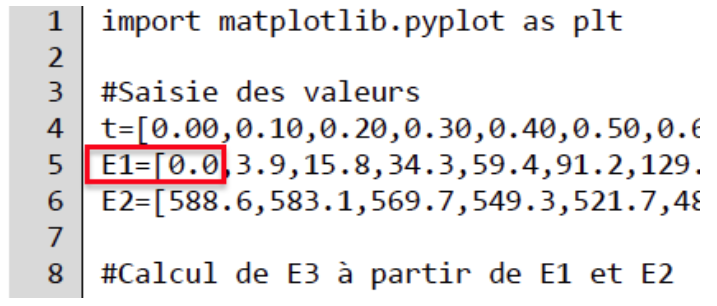
4	t=[0.00,0.10,0.20,0.30,0.40,0.50,0.60,0.70,0.80,0.90,1.00,1.10,1.20,1.30,1.35]
5	E1=[0.0,3.9,15.8,34.3,59.4,91.2,129.6,174.6,226.2,284.5,349.3,420.8,498.9,540.5]
6	E2=[588.6,583.1,569.7,549.3,521.7,487.1,445.4,396.6,340.7,277.8,207.7,130.6,46.4,1.6]
7
8	#Calcul de E3 à partir de E1 et E2
9	E3=[]
10	for i in range(len(t)):
11	Ebis=E1[i]+E2[i]
12	E3.append(Ebis)
13
14	plt.axes()
15	plt.plot(t, E1, 'r+-')
16	plt.plot(t, E2, 'go-')
17	plt.plot(t, E3, 'bv-')
18	plt.xlabel('Temps (s)')
19	plt.ylabel('Énergies (J)')
20	plt.title('Évolution temporelle des énergies du système')
21	plt.grid()
23	plt.show()

Les courbes ci-dessous sont obtenues à partir de l’exécution de ce script. Évolution temporelle des énergies du système :

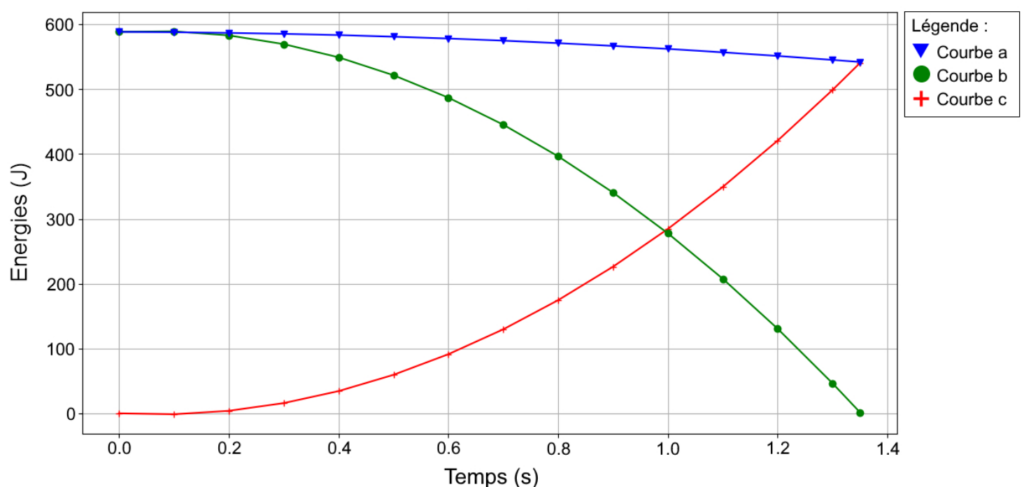
Q.1. À l’aide du script en langage de programmation Python, nommer en justifiant les énergies correspondant à E₁, E₂ et E₃. Attribuer ces énergies aux courbes du graphique ci-dessus (courbes a, b et c).

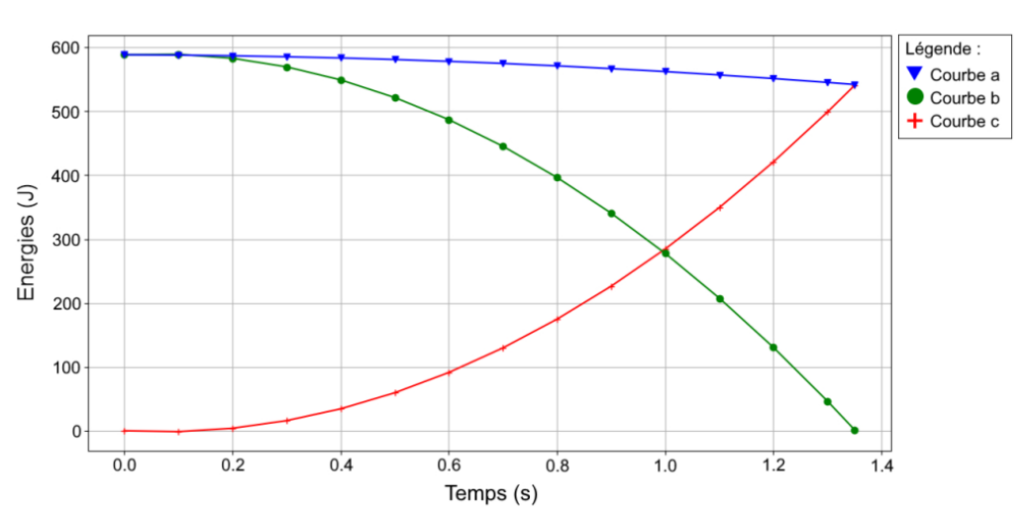
Q.2. Interpréter l’évolution temporelle de l’énergie E₃ représentée sur le graphique ci-dessus.

La diminution de l’énergie mécanique au cours du temps est due aux forces de frottements.

Q.3. Déterminer la valeur de la vitesse atteinte par le skateboardeur au point B.

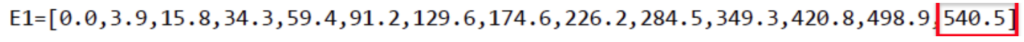
$E_c\left(B\right)=\frac{1}{2}\times m\times v_B^2$
$\frac{1}{2}\times m\times v_B^2=E_c\left(B\right)$
$v_B^2=\frac{2\times E_c\left(B\right)}{m}$
$v_B=\sqrt{\frac{2\times E_c\left(B\right)}{m}}$
$v_B=\sqrt{\frac{2\times540,5}{75,0}}$
$v_B=3,80\ \text{m.s}^{-1}$

B. Phase de mouvement horizontal

Durant la phase de mouvement entre les points B et C, Le skateboardeur glisse jusqu’à s’arrêter au point C. Les forces de frottement liées à l’air sont toujours négligées. Le skateboardeur est notamment soumis à une force de frottement $\overrightarrow{f}$ qui s’oppose au mouvement.

On définit µ_c le coefficient de frottement cinétique tel que :

$\mu_c=\frac{f}{R}$

avec :

• f : norme de la force de frottement ;
• R : norme de la réaction normale au plan.

Données :

• coefficient de frottement cinétique : µ_c = 0,040 ;
• vitesse du skateboardeur au point B : v_B = 3,8 m·s^-1 ;
• théorème de l’énergie cinétique : la variation d’énergie cinétique d’un système entre deux positions A et B est égale à la somme des travaux des forces appliquées à ce système entre les deux positions A et B.

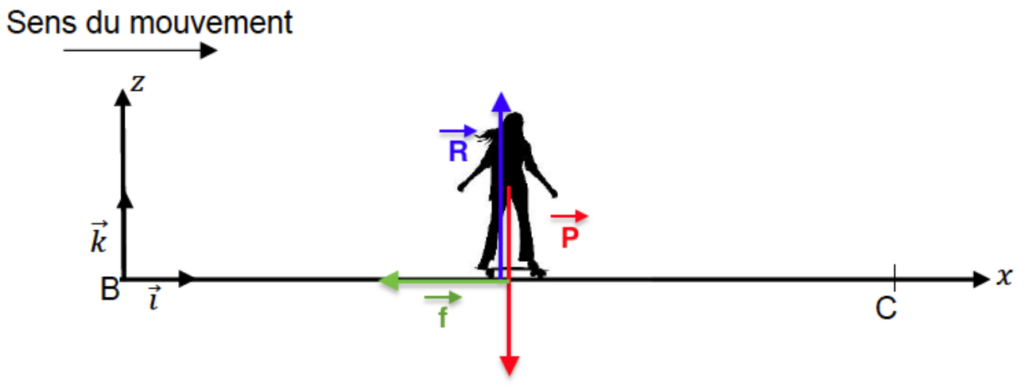
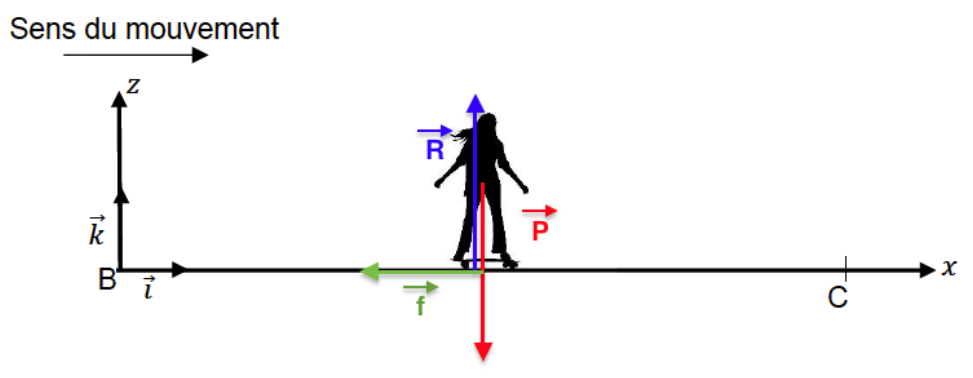
Q.4. Faire l’inventaire des forces extérieures appliquées au skateboardeur et les représenter sans souci d’échelle sur la copie.

Inventaire des forces extérieures appliquées au skateboardeur :
Le poids $\overrightarrow{P}$
La réaction normale du support $\overrightarrow{R}$
La force de frottement $\overrightarrow{f}$

Q.5. À l’aide du théorème de l’énergie cinétique appliqué entre les points B et C, établir la relation entre v_B, m, f et la distance d’arrêt BC.

Théorème de l’énergie cinétique appliqué entre les points B et C :
$\Delta E_C=\Sigma W_{BC}\left(\overrightarrow{F}\right)$
$E_{C\ finale}-E_{C\ initiale}=W_{BC}\left(\overrightarrow{P}\right)+W_{BC}\left(\overrightarrow{R}\right)+W_{BC}\left(\overrightarrow{f}\right)$
$E_C\left(C\right)-E_C\left(B\right)=\overrightarrow{P}\cdot\overrightarrow{BC}+\overrightarrow{R}\cdot\overrightarrow{BC}+\overrightarrow{f}\cdot\overrightarrow{BC}$

Or $\overrightarrow{P}$ est perpendiculaire à $\overrightarrow{BC}$ donc $\overrightarrow{P}\cdot\overrightarrow{BC}=0$
et $\overrightarrow{R}$ est perpendiculaire à $\overrightarrow{BC}$ donc $\overrightarrow{R}\cdot\overrightarrow{BC}=0$
$E_C\left(C\right)-E_C\left(B\right)=\overrightarrow{f}\cdot\overrightarrow{BC}$
$\frac{1}{2}\times m\times v_C^2-\frac{1}{2}\times m\times v_B^2=\overrightarrow{f}\cdot\overrightarrow{BC}$
Or le skateboardeur glisse jusqu’à s’arrêter au point C ainsi $v_C=0\ \text{m.s}^{-1}$
$0-\frac{1}{2}\times m\times v_B^2=\overrightarrow{f}\cdot\overrightarrow{BC}$
$-\frac{1}{2}\times m\times v_B^2=f\times BC\times\cos\left(180\right)$
$-\frac{1}{2}\times m\times v_B^2=-f\times BC$
$\frac{1}{2}\times m\times v_B^2=f\times BC$

Q.6. Montrer que la distance d’arrêt BC s’exprime par la relation :

$$BC=\frac{v_B^2}{2\cdot\mu_c\cdot g}$$

$\frac{1}{2}\times m\times v_B^2=f\times BC$
$f\times BC=\frac{1}{2}\times m\times v_B^2$
Or
$\mu_C=\frac{f}{R}$
$f=\mu_C\times R$

Donc :
$\mu_C\times R\times BC=\frac{1}{2}\times m\times v_B^2$
$BC=\frac{m\times v_B^2}{2\times\mu_C\times R}$

Q.7. Calculer la valeur de la distance d’arrêt.

$BC=\frac{v_B^2}{2\times\mu_C\times g}$
$BC=\frac{{3,8}^2}{2\times0,040\times9,81}$
$BC=18\ \text{m}$

Les roues de skateboard sont réalisées en polyuréthane et sont caractérisées par leur dureté. Plus les roues sont « dures » plus les frottements sont faibles.

Un skateboardeur choisit de remplacer les roues habituelles de son skateboard par des roues moins dures de même géométrie.

Q.8. Indiquer en justifiant comment évolue la distance d’arrêt du skateboard suite à ce changement de roues.

Un skateboardeur choisit de remplacer les roues habituelles de son skateboard par des roues moins dures de même géométrie
Or, d’après l’énoncé : « Plus les roues sont « dures » plus les frottements sont faibles. »
Ainsi, avec des roues moins dures de même géométrie, la force de frottement augmente.

Or
$BC=\frac{v_B^2}{2\times\mu_C\times g}$
$\mu_C=\frac{f}{R}$
$BC=\frac{v_B^2}{2\times\frac{f}{R}\times g}$
$BC=\frac{v_B^2}{2\times g}\times\frac{R}{f}$

La distance d’arrêt du skateboard est inversement proportionnelle à la force de frottement

Lorsque la force de frottement augmente BC diminue.

Ainsi, la distance d’arrêt du skateboard diminue lorsqu’il choisit de remplacer les roues habituelles de son skateboard par des roues moins dures de même géométrie

C. Étude d’un saut et photographie

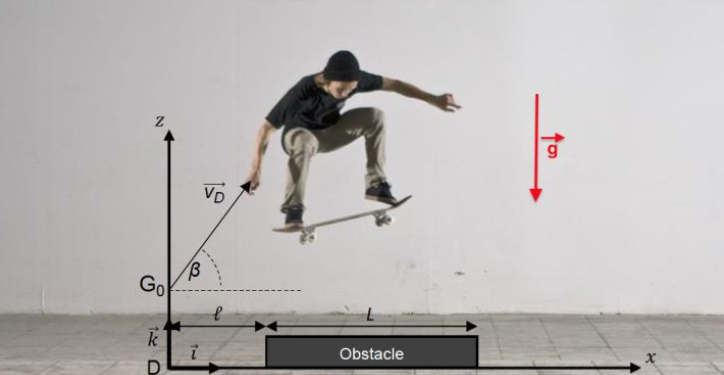
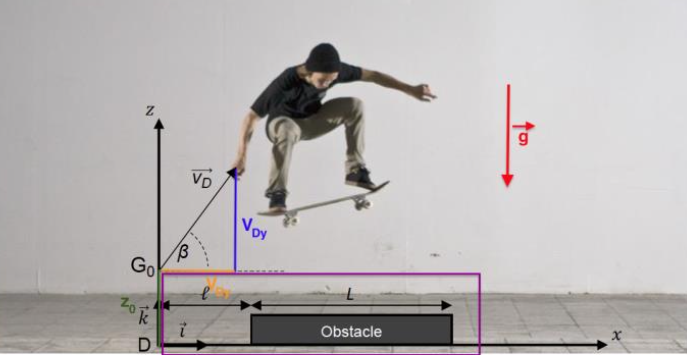
Le skateboardeur arrive à la verticale du point D et déclenche un saut par-dessus un obstacle de longueur L et de faible hauteur. Le centre de masse G0 du skateboardeur a alors pour coordonnées z₀ = 80 cm et x₀ = 0 et sa vitesse est notée $\overrightarrow{v_D}$. Le début de l’obstacle est à une distance ℓ du point D. Durant le saut, l’action exercée par l’air sur le système est considérée comme négligeable.

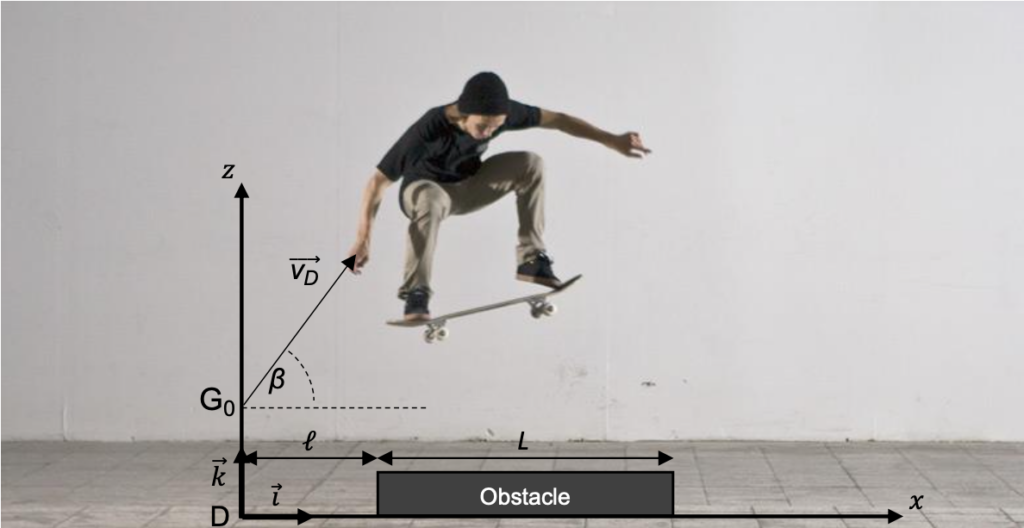
Figure 2. Représentation de la situation sans souci d’échelle

Dans cette partie, on souhaite vérifier si le skateboardeur franchit l’obstacle.

Données : ℓ = 0,70 m et L = 1,0 m.

Q.9. En appliquant la deuxième loi de Newton, établir les équations horaires décrivant la trajectoire du centre de masse G du skateboardeur lors du saut.

Système : skateboardeur
Référentiel terrestre supposé galiléen.

D’après la deuxième loi de Newton :
$\Sigma\overrightarrow{F_{ext}}=m\overrightarrow{a}$
$\overrightarrow{P}=m\overrightarrow{a}$
$m\overrightarrow{g}=m\overrightarrow{a}$
$\overrightarrow{g}=\overrightarrow{a}$

Le vecteur accélération du centre d’inertie du solide est égal au vecteur champ de pesanteur.

$$
\overrightarrow{a}\begin{cases}
a_{x(t)}=0\\
a_{z(t)}=-g
\end{cases}
$$

$\overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}$

On intègre le système d’équation précédent :
$$
\overrightarrow{v}\begin{cases}
v_{x(t)}=C_1\\
v_{z(t)}=-gt+C_2
\end{cases}
$$

d’ou

$$
\overrightarrow{v}\begin{cases}
v_{x(t)}=v_D\cos\beta\\
v_{z(t)}=-gt+v_D\sin\beta
\end{cases}
$$

$\overrightarrow{v}=\frac{d\overrightarrow{OG}}{dt}$

On intègre le système d’équation précédent :
$$
\overrightarrow{OG}(t)\begin{cases}
x(t)=v_D\times\cos\left(\beta\right)\times t+C_3\\
z(t)=-\frac{1}{2}\times g\times t^2+v_D\times\sin\left(\beta\right)\times t+C_4
\end{cases}
$$

d’ou

$$
\overrightarrow{OG}(t)\begin{cases}
x(t)=v_D\times\cos\left(\beta\right)\times t\\
z(t)=-\frac{1}{2}\times g\times t^2+v_D\times\sin\left(\beta\right)\times t+z_0
\end{cases}
$$

Q.10. Montrer que l’équation de la trajectoire du centre de masse G s’écrit sous la forme :

$$z(x)=-\frac{g}{2\cdot v_D^2\cdot\cos^2(\beta)}\cdot x^2+(\tan\beta)\cdot x+z_0$$

On isole $t$ :
$x=v_D\cos\left(\beta\right)\times t$
$t=\frac{x}{v_D\cos\left(\beta\right)}$

On remplace $t$ dans $z$ :
$z(x)=-\frac{g}{2\times v_D^2\cos^2\left(\beta\right)}\times x^2+\tan\left(\beta\right)\times x+z_0$

L’équation de la trajectoire est modélisée par l’équation suivante, x et z étant exprimées en m :

z(x) = – 0,894 x² + 1,22 x + 0,80

Q.11. Calculer la valeur de la coordonnée x du centre de masse lorsque le skateboardeur retrouve l’altitude initiale z = z₀.

$z(x)=-0,894\ x^2+1,22\ x+0,80$

Lorsque le skateboardeur retrouve l’altitude initiale $z=z_0$ :
$0=-0,894\ x^2+1,22\ x$
$x=1,36\ \text{m}$

Q.12. En déduire si le skateboardeur franchira ou pas l’obstacle.

Un photographe amateur souhaite photographier le skateboardeur pendant le saut décrit précédemment. Il est équipé d’un appareil photographique muni d’un flash (voir ci-contre).

Les éléments essentiels d’un flash sont le condensateur et le tube néon émettant un flash lumineux puissant lorsque le condensateur se décharge.

On peut représenter par un schéma électrique simplifié le fonctionnement du flash. L’interrupteur K permet la charge du condensateur de capacité C quand celui-ci est en position 1. Le déclenchement par le photographe bascule l’interrupteur sur la position 2 permettant ainsi la décharge du condensateur dans le tube néon considéré alors comme un conducteur ohmique de résistance R.

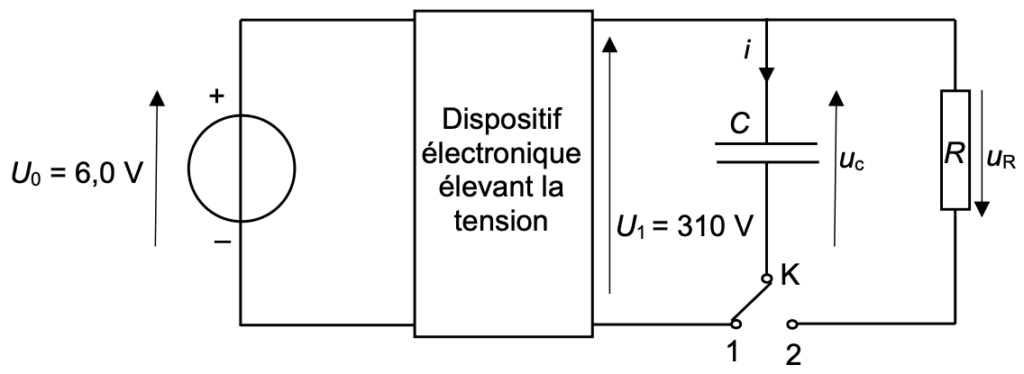
Q.13. Montrer que l’équation différentielle modélisant l’évolution de la tension u_c aux bornes du condensateur lors de sa décharge peut s’écrire :

$$\frac{du_c}{dt}+\frac{1}{\tau}u_c=0$$

où τ est une constante.

Lors de sa décharge, l’interrupteur est sur la position 2
D’après la loi d’additivité des tensions ou loi des mailles :
$U_C\left(t\right)+U_r\left(t\right)=0$
or $U_R(t)=R\times i$
D’ou
$U_C\left(t\right)+R\times i=0$
Or
$i\left(t\right)=\frac{dq_{(t)}}{dt}$

D’ou
$U_C\left(t\right)+R\times\frac{dq_{(t)}}{dt}=0$

Or
$q(t)=C\times U_C(t)$

D’ou
$U_C\left(t\right)+R\times\frac{dC\times U_C(t)}{dt}=0$

$U_C\left(t\right)+R\times C\frac{dU_C(t)}{dt}=0$

$\frac{1}{R\times C}U_C\left(t\right)+\frac{R\times C}{R\times C}\frac{dU_C(t)}{dt}=\frac{0}{R\times C}$
$\frac{1}{R\times C}U_C\left(t\right)+\frac{dU_C(t)}{dt}=0$
$\frac{dU_C(t)}{dt}+\frac{1}{R\times C}U_C\left(t\right)=0$

L’équation différentielle modélisant l’évolution de la tension uc aux bornes du condensateur lors de sa décharge peut s’écrire :
$$\frac{dU_C(t)}{dt}+\frac{1}{\tau}U_C\left(t\right)=0$$

Avec $\tau=R\times C$

Q.14. Vérifier que l’équation différentielle admet une solution de la forme u(t) = A·e-t⁄B. Exprimer les constantes A et B en fonction de paramètres du circuit électrique.

Vérifions que la solution de cette équation différentielle est de la forme :
$U_C\left(t\right)=A\cdot e^{-\frac{t}{B}}$

-Dérivons $U_C\left(t\right)$ :

$\frac{dU_C(t)}{dt}=A\times\left(\frac{-1}{B}\right)\cdot e^{-\frac{t}{B}}$
$\frac{dU_C(t)}{dt}=-\frac{A}{B}\cdot e^{-\frac{t}{B}}$

-Remplaçons $U_C\left(t\right)$ et $\frac{dU_C(t)}{dt}$ dans l’équation :
$\frac{dU_C(t)}{dt}+\frac{1}{\tau}U_C\left(t\right)=0$
$-\frac{A}{B}\cdot e^{-\frac{t}{B}}+\frac{1}{\tau}A\cdot e^{-\frac{t}{B}}=0$
$A\cdot e^{-\frac{t}{B}}\left[-\frac{1}{B}+\frac{1}{\tau}\right]=0$

Un produit de facteur est nul si un de ses facteurs est nul :

$-\frac{1}{B}+\frac{1}{\tau}=0$
$-\frac{1}{B}=-\frac{1}{\tau}$
$B=\tau$

La solution de cette équation différentielle est bien de la forme : $U_C\left(t\right)=A\cdot e^{-\frac{t}{B}}$

Trouvons A avec les conditions initiales :
$U_C\left(t=0\right)=A\cdot e^{-\frac{0}{B}}$
$U_C\left(t=0\right)=A$
$A=U_C(0)$

Soit $U_C\left(t\right)=U_C(0)\cdot e^{-\frac{t}{\tau}}$

Q.15. Montrer que la constante τ est homogène à un temps.

Analyse dimensionnelle :
$\left[\tau\right]=\left[R\right]\left[C\right]$

Avec
$\left[R\right]=\frac{\left[U\right]}{\left[i\right]}$
Et
$\left[C\right]=\frac{\left[q\right]}{\left[U\right]}$

$\left[\tau\right]=\frac{\left[U\right]}{\left[i\right]}\frac{\left[q\right]}{\left[U\right]}$
$\left[\tau\right]=\frac{\left[q\right]}{\left[i\right]}$

Avec $\left[i\right]=\frac{\left[q\right]}{\left[T\right]}$
$\left[\tau\right]=\frac{\left[q\right]}{\frac{\left[q\right]}{\left[T\right]}}$
$\left[\tau\right]=\left[T\right]$
$\left[\tau\right]=s$

La constante τ est homogène à un temps.

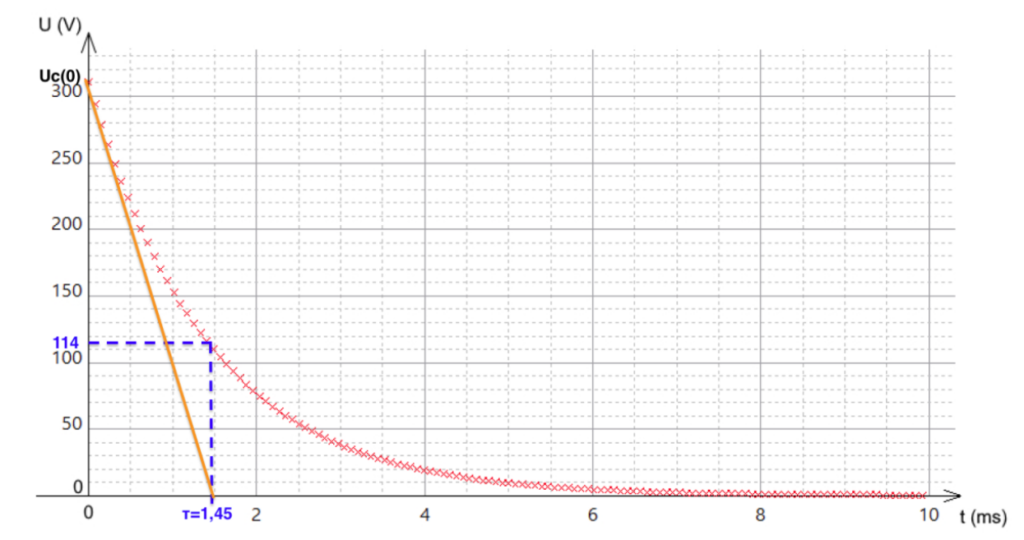
On fournit la courbe de décharge du condensateur.

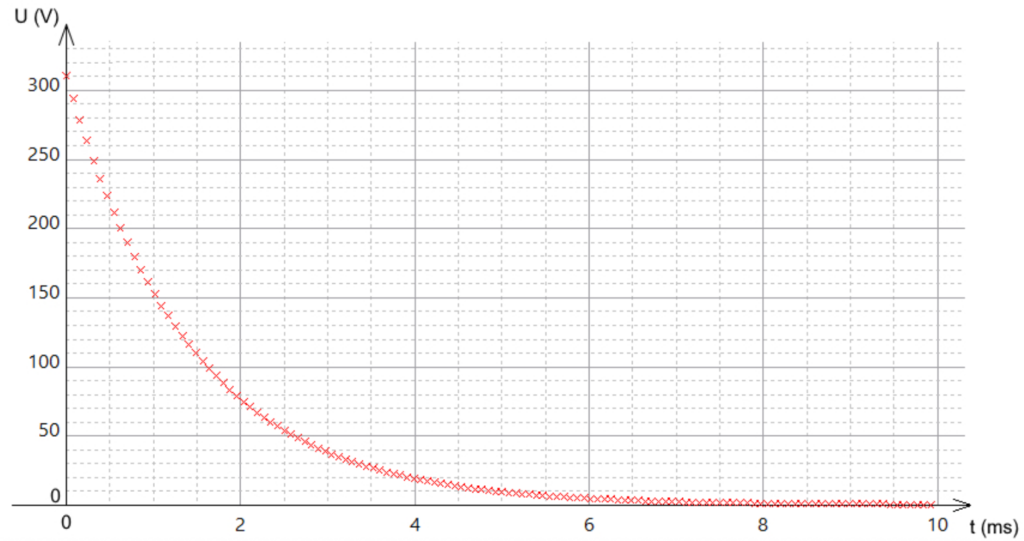
Déterminer la valeur de la constante de temps τ en expliquant la méthode graphique employée.

La durée qui sépare le déclenchement de la photographie et la prise réelle de la photographie est d’environ 5τ , soit 7,5 ms. La photographie est déclenchée lorsque le skateboardeur passe en D. Le saut peut être décomposé en trois étapes : avant l’obstacle, au-dessus de l’obstacle, après l’obstacle. Pour cette étude on prendra : v_D = 3,5 m·s^-1 et β = 50,7°.

Q.17. Déterminer parmi les trois étapes, celle qui est photographiée.

Le candidat est invité à prendre des initiatives et à présenter la démarche suivie même si elle n’a pas abouti.