Bac Amérique du Sud 2022 Sujet 1
Exercice B – (5 points) – Au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n°22-PYCJ1AS1
Sujet et corrigé
EXERCICE B. DÉFIBRILLATEUR CARDIAQUE IMPLANTABLE
Mots-clés : charge et décharge d’un condensateur, temps caractéristique, équation différentielle.
La défibrillation est une méthode utilisée afin de régulariser le rythme cardiaque. Elle consiste à appliquer un « choc électrique » très bref au cœur du patient. Un défibrillateur interne est un petit boitier qui est implanté dans le thorax du patient. Ce boitier comporte trois éléments fondamentaux :
- une pile au lithium permettant l’apport d’énergie nécessaire au fonctionnement du dispositif. Cette pile délivre une tension à vide 𝑈𝑔 = 3,0 V ;
- des circuits électroniques permettant, entre autres choses, d’analyser le rythme cardiaque du patient, de reconnaître des troubles et de déclencher un choc en cas de nécessité ;
- des condensateurs qui permettent de stocker l’énergie qui sera délivrée lors d’un choc ;
- des électrodes qui relient le dispositif au cœur du patient.
Le défibrillateur peut être modélisé par le circuit ci-dessous.
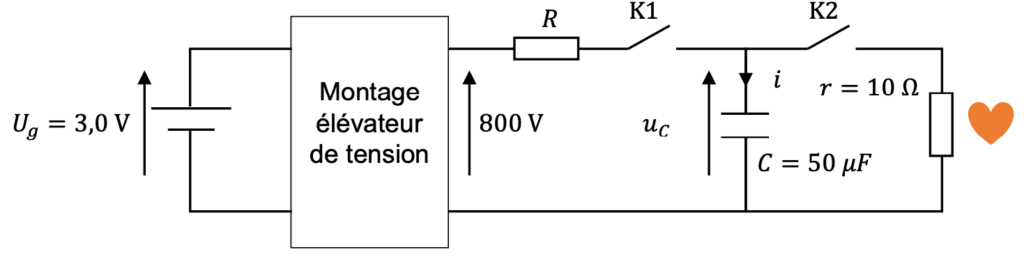
Le fonctionnement du défibrillateur se décompose en deux phases :
- dans la première phase, l’interrupteur K1 est fermé pendant que K2 est ouvert ; au début de cette phase, pris comme origine des temps, le condensateur est déchargé ;
- dans la seconde phase, l’interrupteur K2 est fermé pendant que K1 est ouvert ; c’est dans cette phase que le choc a lieu. La résistance 𝑟 modélise le comportement électrique du cœur.
1. Les quatre graphiques à la page suivante représentent des évolutions possibles de la tension aux bornes du condensateur en fonction du temps. Déterminer celui qui correspond à la première phase de fonctionnement en justifiant la réponse.
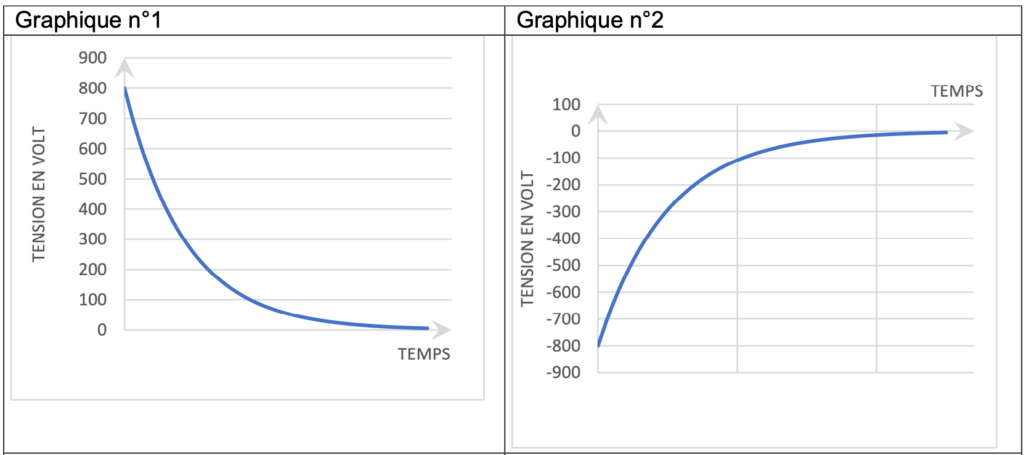
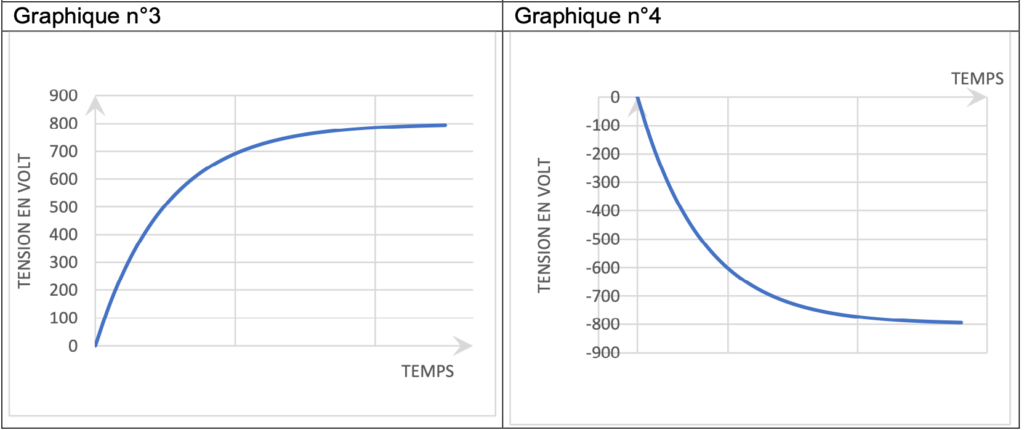
Le condensateur est initialement déchargé. U(0)=0V
On élimine les graphiques 1 et 2.
Le condensateur se charge. la tension augmente au cours du temps.
On élimine le graphiques 4.
Celui qui correspond à la première phase de fonctionnement est le graphique 3.

À l’issue de la première phase, la charge du condensateur étant terminée, on passe à la deuxième phase de fonctionnement.
2. Établir l’équation différentielle vérifiée par la tension 𝑢𝐶(𝑡) lors de cette seconde phase.
« Dans la seconde phase, l’interrupteur K2 est fermé pendant que K1 est ouvert ; c’est dans cette phase que le choc a lieu. La résistance 𝑟 modélise le comportement électrique du cœur »
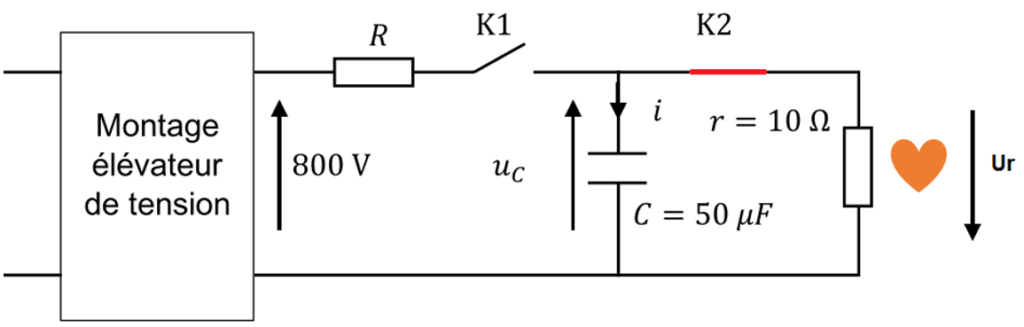
D’après la loi d’additivité des tensions ou loi des mailles :
$U_C\left(t\right)+U_r\left(t\right)=0$
or $U_R(t)=r\times i$
D’ou
$U_C\left(t\right)+r\times i=0$
Or
$i\left(t\right)=\frac{dq_{(t)}}{dt}$
D’ou
$U_C\left(t\right)+r\times\frac{dq_{(t)}}{dt}=0$
Or
$q(t)=C\times U_C(t)$
D’ou
$U_C\left(t\right)+r\times\frac{dC\times U_C(t)}{dt}=0$
$U_C\left(t\right)+r\times C\frac{dU_C(t)}{dt}=0$
3. À la date 𝑡1 l’interrupteur K2 est fermé. Vérifier que la solution de cette équation différentielle peut s’écrire sous la forme :
$$u_C(t)=A\cdot\exp!\left(-\frac{t-t_1}{\tau}\right)$$
Exprimer le temps caractéristique 𝜏 en fonction de 𝑟 et 𝐶 et calculer sa valeur.
Vérifions que la solution de cette équation différentielle peut s’écrire sous la forme :
$U_C\left(t\right)=A\times exp\left(-\frac{\left(t-t_1\right)}{\tau}\right)$
Dérivons Uc(t) :
$\frac{dU_C(t)}{dt}=A\times-\frac{1}{\tau}\times exp\left(-\frac{\left(t-t_1\right)}{\tau}\right)$
Remplaçons les dans l’équation différentielle :
$U_C\left(t\right)+r\times C\frac{dU_C(t)}{dt}=0$
$A\times exp\left(-\frac{\left(t-t_1\right)}{\tau}\right)+r\times C\times A\times-\frac{1}{\tau}\times exp\left(-\frac{\left(t-t_1\right)}{\tau}\right)=0$
$A\times exp\left(-\frac{\left(t-t_1\right)}{\tau}\right)\left[1-\frac{r\times C}{\tau}\right]=0$
Cette équation s’annule à condition que
$1-\frac{r\times C}{\tau}=0$
$-\frac{r\times C}{\tau}=-1$
$r\times C=\tau$
$\tau=r\times C$
$\tau=10\times50{.10}^{-6}$
$\tau=5,0{.10}^{-4}s$
La solution de cette équation différentielle peut s’écrire sous la forme :
$U_C\left(t\right)=A\times exp\left(-\frac{\left(t-t_1\right)}{\tau}\right)$ avec $\tau=r\times C$ .
4. Déterminer la valeur du paramètre 𝐴 sachant qu’à l’instant 𝑡 = 𝑡1, la tension aux bornes du condensateur 𝑢𝐶(𝑡1) vaut 800 V.
A l’instant $t=t_1$ , la tension aux bornes du condensateur $u_C(t_1)$ vaut 800 V.
$U_C\left(t=t_1\right)=800\ V$
$U_C\left(t=t_1\right)=A\times exp\left(-\frac{\left(t_1-t_1\right)}{\tau}\right)$
$U_C\left(t=t_1\right)=A\times exp\left(-\frac{\left(0\right)}{\tau}\right)$
$U_C\left(t=t_1\right)=A$
Donc $A=800\ V$
5. Estimer la durée approximative du « choc électrique ». Commenter.
On considère qu’un condensateur se décharge pour une durée $t_{décharge}=5\tau$ :
$t_{décharge}=5\tau$
$t_{décharge}=5\times5,0.10^{-4}$
$t_{décharge}=2,5.10^{-3}s$
$t_{décharge}=2,5\ ms$
D’après l’énoncé : « Elle consiste à appliquer un « choc électrique » très bref au cœur du patient. »
La durée approximative $t_{décharge}=2,5\ ms$ du « choc électrique » est cohérente avec les données de l’énoncé.
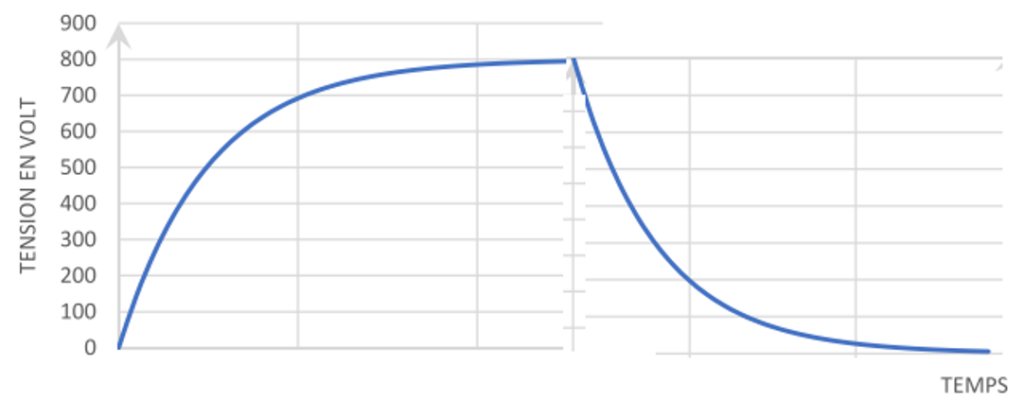
6. Donner l’allure de la tension aux bornes du condensateur en fonction du temps lors d’un cycle complet charge – décharge du condensateur.
Lors d’une charge la tension du condensateur augmente.
Lors d’une décharge la tension du condensateur diminue.
Allure de la tension aux bornes du condensateur en fonction du temps lors d’un cycle complet charge – décharge du condensateur :