Enseignement scientifique première
Durée 1h – 10 points – Thème « La Terre, un astre singulier »
[latexpage]
fascinent les humains. Depuis l’antiquité, les phases de la Lune et ses éclipses ont permis d’en étudier quelques caractéristiques.
Cet exercice s’intéresse aux phases de la Lune ainsi qu’à une méthode géométrique pour déterminer son rayon.
Partie A – Les phases de la Lune
La Lune tourne autour de la Terre sur une orbite quasi-circulaire, avec une période de révolution de 27 jours, 7 h et 43 min. Dans le même temps, la Terre poursuit son mouvement sur une orbite quasi-circulaire autour du Soleil.
Pour un observateur terrestre, la position relative des trois astres engendre un aspect de la lune qui varie au cours du temps et que l’on appelle les « phases de la Lune ». Ce cycle au bout duquel la Lune retrouve son aspect initial, s’appelle la lunaison, et dure 29 jours, 12 h et 44 min.
Document 1. Le schéma ci-dessous représente quelques positions de la Terre et de la Lune lors d’une lunaison. Le Soleil est considéré comme fixe et on en a représenté quelques rayons.
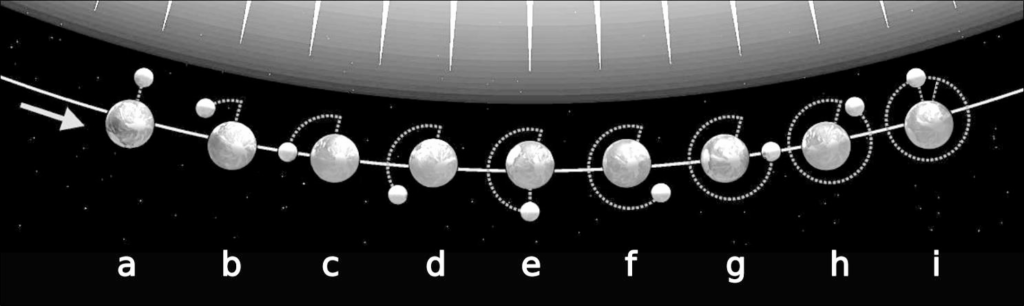
D’après commons.wikimedia.org/wiki/File:Moon_phases_00.jpg
1 – Indiquer à quelles positions de (a) à (i) sur le document 1 correspondent les aspects suivants de la Lune :
| Lune gibbeuse | Premier quartier | Dernier croissant |
|---|---|---|
 |  |  |
| Lune gibbeuse | Premier quartier | Dernier croissant |
|---|---|---|
 |  |  |
| Position f | Position c | Position h |
2 – Les positions (a) et (i), positions extrêmes d’un cycle de lunaison du document 1, correspondent aux situations appelées « nouvelle Lune ». Préciser ce qu’on observe alors depuis la Terre.
Les positions (a) et (i) correspondent aux situations appelées « nouvelle Lune ». On observe alors plus la lune depuis la Terre.
3 – La Lune présente toujours la même face à la Terre. Choisir, parmi les propositions suivantes, la période de rotation de la Lune sur elle-même. On pourra s’aider d’un schéma.
| 365,25 jours | 24 h | 27 jours 7 h et 43 min | 29 jours 12 h et 44 min |
La Lune présente toujours la même face à la Terre. D’après l’énoncé : La Lune tourne autour de la Terre sur une orbite quasi-circulaire, avec une période de révolution de 27 jours, 7 h et 43 min.
Pour présenter la même face à la terre la période de rotation de la Lune sur elle-même est identique à sa période de révolution soit 27 jours 7 h et 43 min.
4 – Parmi les situations de (a) à (i) du document 1, certaines permettent l’observation d’éclipses de Lune. Préciser laquelle ou lesquelles.
Les éclipses de Lune ont lieu au moment de la pleine Lune. La lune est dans le cône d’ombre de la terre.
La situation qui permet l’observation d’éclipses de Lune est la situation e.
Partie B – Dimension de la Lune
Document 2. Éclipse de Lune
Aristarque de Samos (310-230 avant JC) émet l’hypothèse qu’en mesurant la taille de l’ombre de la Terre sur la Lune lors d’une éclipse, on peut calculer le rapport entre le rayon de la Terre et le rayon de la Lune.
Il suppose par ailleurs que l’ombre de la Terre sur la Lune a la même taille que la Terre, ce qui revient à considérer que les rayons du Soleil sont parallèles entre eux.

Éclipse de lune du 19 janvier 2019 à Chambord (G. Souvant – AFP)
Document 3. Construction géométrique du centre d’un cercle
Sur le schéma ci-contre, la Lune est modélisée par le cercle C dont on veut déterminer le centre. Pour cela, on choisit 3 points M, N, P sur ce cercle.
La droite D 1 est la médiatrice du segment [MN].
La droite D 2 est la médiatrice du segment [NP].
Ces deux médiatrices se coupent en un point O.
On rappelle que tout point appartenant à la médiatrice d’un segment est situé à égale distance des extrémités de ce segment.
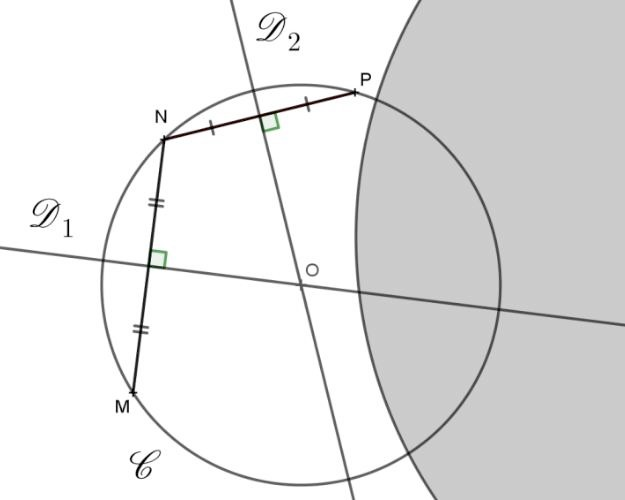
Schéma de la Lune partiellement cachée par l’ombre de la Terre
5 – Démontrer que O est le centre du cercle C .
Tout point appartenant à la médiatrice d’un segment est situé à égale distance des extrémités de ce segment.
O appartient à la médiatrice du segment [MN] il est donc à égale distance de M et N
O appartient à la médiatrice du segment [NP] il est donc à égale distance de N et P.
Le point O est à égale distance des points M, N et P qui sont situés sur le cercle.
Ainsi, O est le centre du cercle C.
6 – Dans le document donné en annexe, à rendre avec la copie, reproduire cette construction géométrique pour déterminer le centre de la Lune sur la photo, puis réaliser une mesure en centimètres de son rayon rL.

Sur la photo, on mesure de son rayon rL=4,0 cm.
7 – Une construction similaire a permis de mesurer le rayon de la Terre sur la photo.
On admet qu’elle a donné rT ≈ 16,5 cm. Sachant que le rayon RT de la Terre vaut 6400 km, déterminer une valeur (en km) du rayon RL de la Lune.
| Photo | Réel | |
| Terre | rT≈ 16,5 cm | RT=6400 km |
| Lune | rL=4,0 cm | RL |
RL=(4,0×6400)/16,5
RL=1551 km
Le rayon RL de la Lune a pour valeur RL=1551 km.
Document réponse à rendre avec la copie
Les phases de la Lune
Question 7

