Enseignement scientifique première
Durée 1h – 10 points – Thème « Une longue histoire de la matière »
[latexpage]
La silice est la forme naturelle du dioxyde de silicium (SiO2) qui entre dans la composition de nombreux minéraux (quartz, etc.). La silice représente 60,6 % de la masse de la croûte terrestre continentale. De nombreuses roches sont constituées de silice (sable, grès, granite, etc.) et l’étude des différentes structures possibles permet d’en savoir plus sur les conditions de formation des roches.
Le verre utilisé dans l’industrie est un solide non cristallin (amorphe), dur, fragile (cassant) et transparent. Sa composition chimique contient une part importante de silice.
Partie A. La silice : une structure amorphe ou cristalline
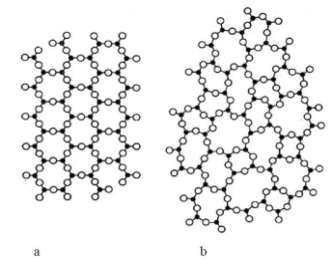
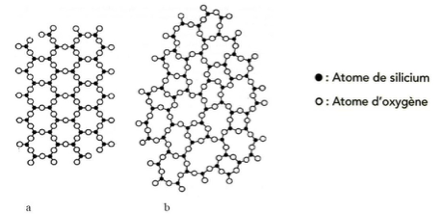
Document 1. Deux structures en coupe de la silice
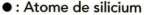
Source : d’après CHAGUETMI, Salem (2010), Élaboration et caractérisation de nouveaux verres de fluorohafnates de strontium et de phosphosulfates. Thèse, Université Mohamed Khider Biskra
1 – La figure du document 1 montre deux structures possibles de la silice. L’une d’elles est dite cristalline, l’autre amorphe (verre). Parmi les représentations a et b, laquelle correspond à une structure cristalline ? Justifier votre choix.
Les cristaux sont des édifices chimiques possédant une structure en trois dimensions parfaitement ordonnée.
La structure cristalline est donc la a.
À partir de deux échantillons identiques de silice liquide, on peut obtenir soit un verre, soit un cristal selon la vitesse de refroidissement.
Document 2. Évolution du volume d’un échantillon de silice lors d’un changement d’état
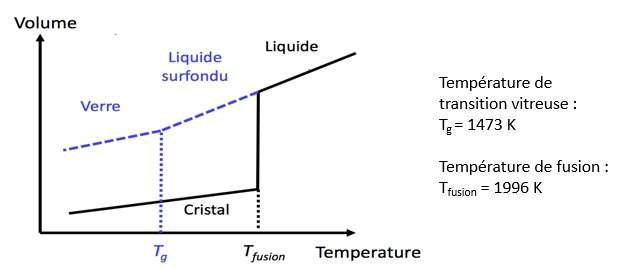
2 – Comparer qualitativement les volumes des deux échantillons obtenus (verre ou cristal) à la température de 1400 K.
A la température de 1400 K le volume du verre est supérieur au volume du cristal.
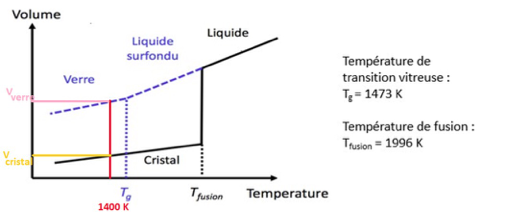
3 – Proposer une explication à cette différence de volume en s’appuyant sur le document 1.
La structure du cristal est ordonnée alors que celle du verre est désordonnée. Cette différence peut expliquer que volume du verre soit supérieur au volume du cristal.
Partie B. Étude de la maille cristalline du silicium
On s’intéresse dans cette partie au silicium pur. On fait l’hypothèse que la structure cristalline du silicium est cubique à faces centrées, avec les caractéristiques suivantes :
Rayon d’un atome de silicium : 𝑟 = 118×10−12 m
Masse d’un atome de silicium : 𝑚 = 4,66×10−26 kg
4 – Le but de cette partie est de déterminer la masse volumique du silicium afin de valider ou d’invalider l’hypothèse formulée sur sa structure (cubique à faces centrées).
Document 3. Coupe d’une maille selon le modèle cubique à faces centrées
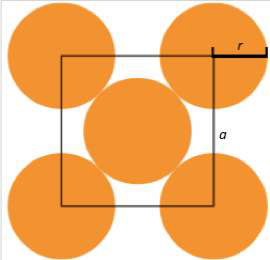
La mesure a correspond au paramètre de la maille et on suppose que les atomes de silicium sont sphériques et tangents. Le rayon d’un atome de silicium est noté r.
4-a- À l’aide de la figure du document 3, démontrer que : a = 2√2𝑟 et calculer sa valeur.
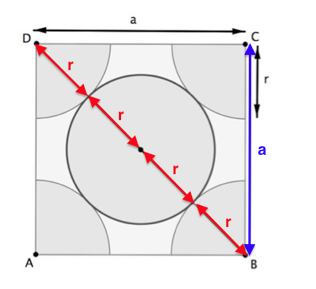
D’après le théorème de Pythagore :
\[\left(4r\right)^2=a^2+a^2\]
\[16r^2=2a^2\]
\[2a^2=16r^2\]
\[a^2=\frac{16r^2}{2}\]
\[a^2=8r^2\]
\[\sqrt{a^2}=\sqrt{8r^2}\]
\[a=\sqrt{8}r\]
\[a=2\sqrt{2}r\]
4-b- Représenter en perspective cavalière la maille cubique à faces centrées.
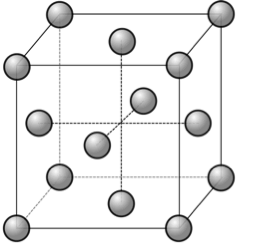
4-c- On rappelle que, dans la structure cubique à faces centrées, une maille contient l’équivalent de 4 atomes de silicium. Calculer la masse volumique d’un cristal de silicium dans cette hypothèse.
\[\rho=\frac{m_{maille}}{V_{maille}} \]
Or
\[m_{maille}=N\times m \]
\[V_{maille}=a^3 \]
Non demandé (Dans une structure cubique face centrée : Il y a 8 atomes sur les sommets qui sont dans 1/8 de la maille. Il y a 6 atomes sur les faces qui sont dans 1/2 de la maille. N=8×1/8+6×1/2=4 Il y a 4 atomes dans une maille.)
\[\rho=\frac{N\times m}{a^3} \]
\[\rho=\frac{4\times m}{(2\sqrt{2}r)^3} \]
\[\rho=\frac{4\times 4,66\times 10{-26}}{(2\sqrt{2} \times 118 \times 10{-12})^3} \]
\[\rho=5014 kg.m^{-3}} \]
4-d- En réalité, la masse volumique du cristal de silicium est 2,33 g.cm-3. L’hypothèse de la structure cristalline cubique à faces centrées peut-elle être validée ?
ρ=5014 kg〖.m〗^(-3)
ρ=5,014.103 kg.m-3
ρ=5,014 g.cm-3
La masse volumique du cristal de silicium est 2,33 g.cm-3: elle est différente de celle calculée si le cristal de silicium possédait une structure cubique à faces centrées.
Le cristal de silicium ne possède pas une structure cubique à faces centrées.
L’hypothèse de la structure cristalline cubique à faces centrées n’est pas être validée.
