Bac Amérique du nord 2023 Sujet 2
Exercice 1 – (11 points) – Durée 1h45 – Calculatrice autorisée
Sujet n°23-PYCJ2AN1
Sujet et corrigé
EXERCICE 1 : BICYCLE MOTO CROSS (11 POINTS)
Le BMX (Bicycle Moto Cross) est une discipline cycliste née aux USA et importée en France dans les années 1980.
La « Race », sport olympique depuis 2008, est une course qui se déroule sur une piste bosselée de longueur comprise entre 270 et 400 m. Huit pilotes partent d’une butte de départ surélevée et doivent terminer le tour le plus rapidement possible en franchissant plusieurs types d’obstacles.

Départ de la finale des J.O de Tokyo (2020)
A. Les signaux associés au départ de la course
Une fois les pilotes bien positionnés sur la grille en haut de la butte, le starter lance la commande automatique de départ, qui comporte une série de 4 bips sonores synchronisés avec des feux (rouge, 1er orange, 2ème orange, vert). Au quatrième bip, qui coïncide avec le feu vert, la grille s’abaisse pour libérer les pilotes.
Lors de cette procédure, le cahier des charges de l’union cycliste internationale impose que le niveau d’intensité sonore soit initialement réglé pour que, malgré l’atténuation acoustique générée par leurs casques, les pilotes puissent tous entendre parfaitement les bips sonores. On considère qu’un son est parfaitement audible par le pilote à partir d’un niveau d’intensité sonore de l’ordre de 60 dB, sans dépasser 85 dB.
Données :
- célérité d’une onde sonore dans l’air à 20 °C : cson = 340 m∙s-1 ;
- célérité d’une onde lumineuse dans l’air : supposée connue ;
- fréquence des bips sonores : f = 632 Hz.
Le haut-parleur délivrant les bips sonores est unique. Il est situé dans le prolongement de la ligne de départ à une distance d = 4,0 m sur la gauche du pilote le plus proche. Le pilote le plus éloigné se trouve alors 7,0 m plus à droite.

Le haut-parleur a été réglé de sorte que le niveau d’intensité sonore du son incident mesuré sur la paroi du casque du premier pilote soit Li1 = 83 dB.
L’atténuation par absorption, correspond à la différence entre le niveau d’intensité sonore Li du son incident sur le casque et le niveau d’intensité sonore Lt du son transmis à l’intérieur de celui-ci. Pour la fréquence 632 Hz et les casques en fibre de carbone utilisés par les pilotes de haut niveau, cette atténuation est de l’ordre de 10 dB.
Q.1. Calculer le niveau d’intensité sonore Lt1 transmis à l’intérieur du casque du premier pilote.
$$L_{T1}=L_{i1}-A$$
$$L_{T1}=83-10$$
$$L_{T1}=73\ dB$$
La relation entre L, le niveau d’intensité sonore à une distance d de la source et L’, le niveau sonore à une distance d’ plus éloignée de cette source, est donnée par : $L’=L+20\cdot\log\left(\frac{d}{d’}\right)$.
Q.2. Calculer le niveau d’intensité sonore Li8 du son incident sur le casque du huitième pilote, puis le niveau d’intensité sonore Lt8 du son transmis correspondant. Commenter ce résultat.
$$L^\prime=L+20\ log\left(\frac{d}{d\prime}\right)$$
$$L_{i8}=L_{i1}+20\ log\left(\frac{d_1}{d_8}\right)$$

$$L_{i8}=83+20\ log\left(\frac{4,0}{11,0}\right)$$
$$L_{i8}=74\ dB$$
En prenant en compte l’atténuation du casque :
$$L_{T8}=L_{i8}-A$$
$$L_{T8}=74-10$$
$$L_{T8}=64\ dB$$
D’après le texte : On considère qu’un son est parfaitement audible par le pilote à partir d’un niveau d’intensité sonore de l’ordre de 60 dB, sans dépasser 85 dB.
Ainsi le son est parfaitement audible par le pilote le plus proche (Q.1.) et le plus éloigné (Q.2.). Les pilotes intermédiaires entendent donc également un son qui est parfaitement audible.
Certaines buttes sont maintenant sonorisées avec deux haut-parleurs, disposés aux extrémités de la ligne de départ.
Q.3. Expliquer qualitativement pourquoi ce dispositif à double haut-parleur est plus équitable.
Calculons le temps mis par le son pour parcourir la distance entre le 1er et le dernier pilote :
$$c_{son}=d\Delta t$$
$$\Delta t=dcson$$
$$\Delta t=7,0340$$
$$\Delta t=2,1\times 10-2s$$
$$\Delta t=21\ ms$$
Le dernier pilote reçoit le son avec 21 ms de retard.
Deux haut-parleurs, disposés aux extrémités de la ligne de départ permettent que le dernier et le 1er pilote reçoivent le son en même temps.
Remarque : Le pilote du milieu recevra le son avec 10 ms de retard (comme dans le cas du système avec un seul haut-parleur).
Ce dispositif à double haut-parleur est donc plus équitable.
Deux rampes de feux lumineux sont installées à mi-pente de la butte de départ de part et d’autre du plan incliné de la descente :

Q.4. Justifier sans calcul l’intérêt pour les pilotes d’être davantage attentifs aux signaux lumineux qu’aux signaux sonores pour prendre le départ.
Les signaux lumineux se déplacent à la vitesse de la lumière. Ainsi, pour cette différence de distance entre les pilotes, le décalage est négligeable.
D’où l’intérêt pour les pilotes d’être davantage attentifs aux signaux lumineux qu’aux signaux sonores pour prendre le départ.
B. Le départ
Lorsque la grille s’abaisse, les pilotes pédalent intensément pour acquérir la plus grande vitesse possible au bas de la butte. Lors d’une séance d’entrainement, filmée pour une chaine sportive, se déroulant sur une piste possédant une butte de départ à 8 m de hauteur, un pilote atteint la vitesse de 61 km∙h-1 au bas de la butte en 2,7 s.
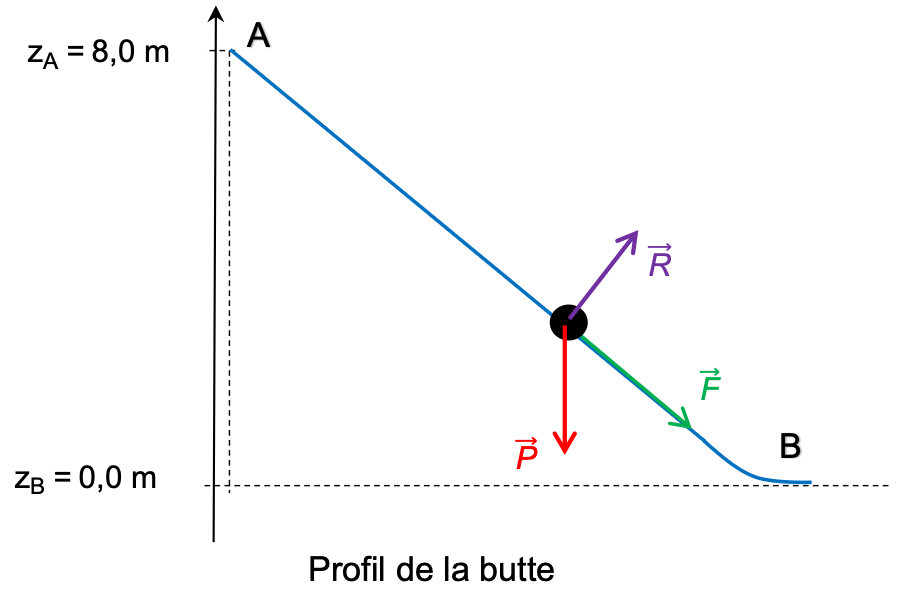
Pendant cette descente, on considère que le système {pilote + bicyclette}, assimilé à un point matériel de masse totale m = 93 kg se déplace de la position A jusqu’à la position B, en n’étant soumis qu’à trois actions mécaniques modélisées par son poids $\overrightarrow{P}$, la réaction $\overrightarrow{R}$ du plan incliné toujours perpendiculaire au plan et la force motrice $\overrightarrow{F}$ de norme supposée constante et parallèle au plan. Le référentiel terrestre est ici considéré comme galiléen.
Données :
- intensité de la pesanteur g = 9,81 m∙s-2 ;
- théorème de l’énergie cinétique : la variation d’énergie cinétique d’un système entre deux positions A et B est égale à la somme des travaux des forces appliquées à ce système entre les deux positions A et B.
Q.5. Appliquer le théorème de l’énergie cinétique au système lors du trajet AB pour exprimer le travail $W_{AB}(\overrightarrow{F})$ de la force motrice liée au pédalage du pilote.
Théorème de l’énergie cinétique : La variation d’énergie cinétique entre deux points A et B est égale a la somme des travaux des forces appliquées à ce système entre les deux positions A et B :
$$\Delta E_C=\Sigma W_{AB}(\overrightarrow{F})$$
$$E_{C\ finale}-E_{C\ initiale}=W_{AB}(\overrightarrow{F})$$
$$E_C\left(B\right)-E_C\left(A\right)=W_{AB}(\overrightarrow{F})+\overrightarrow{P}.\overrightarrow{AB}+\overrightarrow{R}.\overrightarrow{AB}$$
$$\frac{1}{2}\times m\times v_B^2-\frac{1}{2}\times m\times v_A^2=W_{AB}(\overrightarrow{F})+\overrightarrow{P}.\overrightarrow{AB}+R\times AB\times \cos(\theta)$$
Avec :
vA=0 m.s-1
$$\overrightarrow{P}.\overrightarrow{AB}=m\times g\times \left(z_A-z_B\right)$$ le travail du poids
θ=90°: l’angle entre $\overrightarrow{R}$ et $\overrightarrow{AB}$

$$\frac{1}{2}\times m\times v_B^2-\frac{1}{2}\times m\times 0^2=W_{AB}(\overrightarrow{F})+m\times g\times \left(z_A-z_B\right)+R\times AB\times \cos(90)$$
$$\frac{1}{2}\times m\times v_B^2=W_{AB}(\overrightarrow{F})+m\times g\times \left(z_A-z_B\right)+R\times AB\times 0$$
$$\frac{1}{2}\times m\times v_B^2=W_{AB}(\overrightarrow{F})+m\times g\times \left(z_A-z_B\right)$$
$$W_{AB}\left(\overrightarrow{F}\right)+m\times g\times \left(z_A-z_B\right)=\frac{1}{2}\times m\times v_B^2$$
$$W_{AB}\left(\overrightarrow{F}\right)=\frac{1}{2}\times m\times v_B^2-m\times g\times \left(z_A-z_B\right)$$
Q.6. Calculer la valeur de ce travail.
$$W_{AB}\left(\overrightarrow{F}\right)=\frac{1}{2}\times m\times v_B^2-m\times g\times \left(z_A-z_B\right)$$
$$W_{AB}\left(\overrightarrow{F}\right)=\frac{1}{2}\times 93\times \left(\frac{61}{3,6}\right)^2-93\times 9,81\times \left(8,0-0\right)$$
$$W_{AB}\left(\overrightarrow{F}\right)=6,1\times {10}^3J$$
Ce pilote est capable de développer une puissance de pédalage de l’ordre de 2000 à 2500 W lors du trajet AB.
Q.7. Montrer que la valeur du travail calculé à la question Q.6 est en accord avec la puissance de pédalage du pilote, supposée constante.
$$P=\frac{E}{\Delta t}$$
$$P=\frac{W_{AB}\left(\overrightarrow{F}\right)}{\Delta t}$$
$$P=\frac{6,1\times {10}^3}{2,7}$$
$$P=2,3\times {10}^3W$$
La puissance de pédalage est bien comprise entre 2000 à 2500 W. Ainsi, la valeur du travail calculé à la question Q.6 est en accord avec la puissance de pédalage du pilote, supposée constante.
C. Le saut de bosse
Le pilote aborde maintenant une bosse double avec l’objectif de complètement franchir l’obstacle.
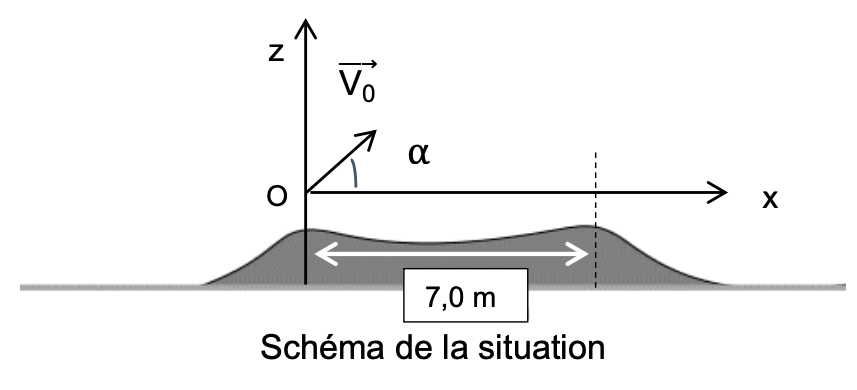
Le vecteur vitesse initiale du système $\overrightarrow{V_0}$ est incliné d’un angle α = 23° par rapport à l’horizontale. Les deux sommets sont situés à la même hauteur et distants de 7,0 m.
À la date t = 0 de son « envol » l’ensemble {pilote + bicyclette}, assimilé à un point matériel noté G, se trouve en O. Sa masse totale vaut m = 93 kg, et la norme de $\overrightarrow{V_0}$ est mesurée à 13,6 m∙s-1.
On néglige l’action de l’air sur l’ensemble {pilote + bicyclette}.
Q.8. En appliquant la deuxième loi de Newton au système, montrer que les équations horaires du mouvement pendant le saut sont :
$$\overrightarrow{OG}\ \begin{cases}
x(t)=(V_0\cdot\cos\alpha)\cdot t\\
z(t)=-\dfrac{1}{2}g\cdot t^2+(V_0\cdot\sin\alpha)\cdot t
\end{cases}$$
Système {pilote + bicyclette}
Référentiel terrestre supposé galiléen
D’après la deuxième loi de newton :
$$\Sigma\overrightarrow{F_{ext}}=m\overrightarrow{a}$$
$$\overrightarrow{P}=m\overrightarrow{a}$$
$$m\overrightarrow{g}=m\overrightarrow{a}$$
$$\overrightarrow{g}=\overrightarrow{a}$$
Or
$$\overrightarrow{g}\left|\begin{matrix}0\\-g\end{matrix}\right.$$
Le vecteur accélération du centre d’inertie du solide est égal au vecteur champ de pesanteur.
$$\overrightarrow{a}\ \left|\begin{matrix}a_{x(t)}=0 \\ {\ a}_{z\left(t\right)}=-g \end{matrix}\right.$$
$$\overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}$$
On intègre le système d’équation précédent :
$$\overrightarrow{v}\ \left|\begin{matrix}v_{x(t)}=C_1 \\ {\ v}_{z\left(t\right)}=-gt+C_2\end{matrix}\right.$$
Pour trouver les constantes, on utilise $$\overrightarrow{v}0$$
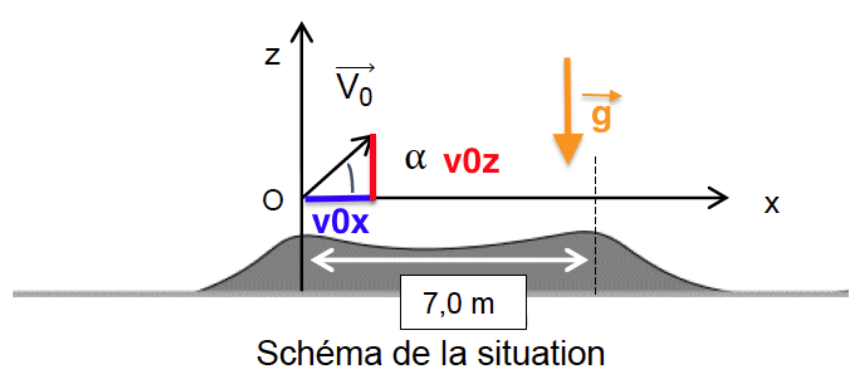
$$\overrightarrow{v}0\ \left|\begin{matrix}v{0x}=v_0\ cos\alpha \\v{0z}=v_0\ sin\ \alpha \end{matrix}\right.$$
d’ou
$$\overrightarrow{v}\ \left|\begin{matrix}v_{x(t)}=v_0\ cos\alpha \\ {\ v}_{z\left(t\right)}=-gt+v_0\ sin\ \alpha \end{matrix}\right.$$
$$\overrightarrow{v}=\frac{d\overrightarrow{OG}}{dt}$$
On intègre le système d’équation précédent :
$$\overrightarrow{OG}\left|\begin{matrix}x\left(t\right)=\ \ v_0\cos(\alpha)\times t\ +C_3 \\ z\left(t\right)=-\frac{1}{2}gt^2+v_0\sin(\alpha)\times t\ +C_4\ \end{matrix}\right.$$
Pour trouver les constantes, on utilise $$\overrightarrow{OG}_0$$
$$\overrightarrow{OG}_0\ \left|\begin{matrix}x_0=0 \\z_0=0\end{matrix}\right.$$
d’ou
$$\overrightarrow{OG}\left|\begin{matrix}x\left(t\right)=\ \ v_0\cos(\alpha)\times t \\ z\left(t\right)=-\frac{1}{2}gt^2+v_0\sin(\alpha)\times t \end{matrix}\right.$$
Le système retrouve le contact avec le sol au bout de 1,0 s.
Q.9. Déterminer si le saut est réussi dans le cadre du modèle utilisé.
Le système retrouve le contact avec le sol au bout de 1,0 s.
$$x\left(t=1,0s\right)=\ \ 13,6\times \cos(23)\times 1,0$$
$$x\left(t=1,0s\right)=\ \ 12,5\ m$$
Les deux sommets sont situés à la même hauteur et distants de 7,0 m. Le pilote atterrie après les deux sommets : le saut est réussi.
En réalité le système entre en contact avec le sol juste après le deuxième sommet, pour une distance horizontale parcourue de l’ordre de 8,0 m.
Q.10. Montrer que le modèle n’est pas adapté à la description du saut et en indiquer une raison possible.
Le modèle prévoit distance horizontale parcourue de 12,5m or en réalité elle est l’ordre de 8,0 m. Ainsi, le modèle n’est pas adapté à la description du saut.
Nous avons négligé néglige l’action de l’air dans ce modèle, c’est une raison qui pourrait expliquer l’écart entre le modèle et la réalité.
D. Une expérience contestée
Après la course, la technique dite du bain froid, est utilisée par des pilotes de BMX pour favoriser la récupération physique. Elle consiste à immerger le pilote de BMX dans un bain d’eau froide à 10 °C, pendant quelques minutes.
Dans cette partie, on cherche à déterminer la température du corps du pilote au bout de la durée d’immersion. Pour cela on s’intéresse à l’évolution de la température T du système {pilote de BMX} placé au contact de l’eau froide du bain dont la température Teau demeure constante et égale à 10 °C.
On note Q l’énergie thermique échangée entre le pilote et l’eau pendant une durée Δt. On note Φ le flux thermique correspondant.
On assimile le pilote à un système incompressible possédant une capacité thermique, C, constante.
Données :
- température initiale du pilote avant son immersion : θ0 = 37 °C ;
- T (K) = θ (°C) + 273 ;
- capacité thermique du système {pilote de BMX} : C = 347 kJ⋅K-1.
Q.11. Citer trois modes de transfert thermique.
Les trois modes de transfert thermique sont :
La conduction
La convection
Le rayonnement
Q.12. En appliquant le premier principe de la thermodynamique, relier la variation d’énergie interne ΔU du système {pilote de BMX} à l’énergie thermique Q.
Premier principe de la thermodynamique :
$$\Delta U=Q+W$$
Ici $$W=0$$
$$\Delta U=Q$$
Q.13. Exprimer le flux thermique Φ en fonction de Q et de Δt. Indiquer les unités du système international des grandeurs intervenant dans cette expression.
flux thermique :
$$\phi=Q\Delta t$$
$$\phi$$ : flux thermique échangé (W)
$$Q$$ : énergie échangée par transfert thermique (J)
$$\Delta t$$ : durée de l’échange (s)
La variation d’énergie interne d’un système incompressible au repos dont la température varie de ΔT est donnée par la relation ΔU = C ∙ ΔT.
Q.14. Exprimer le flux thermique Φ en fonction de la capacité thermique C, de la variation de température ΔT et de la durée Δt.
$$\phi=\frac{Q}{\Delta t}$$
Or
$$Q=\Delta U$$
$$\phi=\frac{\Delta U}{\Delta t}$$
Or
$$\Delta U=C\times \Delta T$$
Donc :
$$\phi=\frac{C\times \Delta T}{\Delta t}$$
La valeur du flux thermique moyen échangé entre le système {pilote de BMX} et l’eau froide est estimée à 4,6 x 103 W.
Q.15. Calculer à l’aide du modèle la température du pilote au bout de 10 min d’immersion dans l’eau froide.
$$\phi=\frac{C\times \Delta T}{\Delta t}$$
$$\frac{C\times \Delta T}{\Delta t}=ϕ$$
$$\Delta T=\frac{ϕ\times \Delta t}{C}$$
$$\Delta T=\frac{4,6\times {10}^3\times 10\times 60}{347\times {10}^3}$$
$$\Delta T=8,0°$$
Température initiale du pilote avant son immersion : θ0 = 37 °C
Température du pilote au bout de 10 min d’immersion dans l’eau froide : 37-8=29°C
Q.16. Indiquer une des raisons expliquant pourquoi ce modèle n’est pas pertinent.
Ce modèle n’est pas pertinent car le corps fournit de l’énergie en burlant des sucres pour maintenir la température du corps proche de 37°C.
