Bac Asie 2023 Sujet 2
Exercice 3 – (5,5 points) – Durée 0h58 – Calculatrice autorisée
Sujet n°23-PYCJ2JA1
Sujet et corrigé
EXERCICE 3 – ETUDE DES AGREGATS D’EAU (5,5 POINTS)
Pour étudier la formation des gouttelettes d’eau dans l’atmosphère, il est possible en laboratoire de reconstituer de très petites gouttelettes contenant quelques dizaines de molécules d’eau, appelées agrégats, et qui peuvent grossir par « collage » de molécules d’eau supplémentaires. La masse de ces agrégats est un paramètre important pour comprendre le mécanisme de formation de la pluie. On cherche donc à mesurer la masse de ces agrégats pour mieux les étudier.

L’objectif de cet exercice est d’illustrer le principe de la détermination de la masse des agrégats par l’utilisation d’un accélérateur linéaire.
Le dispositif expérimental est schématisé figure 1 ci-dessous. On injecte à l’entrée de la zone de collision des agrégats constitués de N = 50 molécules d’eau. Chaque agrégat porte une charge électrique q positive. Les agrégats peuvent subir des collisions avec des molécules d’eau dans cette zone de collision.
On cherche à déterminer la masse des agrégats à la sortie de la zone de collision pour savoir si des molécules d’eau se sont collées aux agrégats. Pour cela, les agrégats passent, après la zone de collision, dans une zone d’accélération constituée de deux armatures métalliques A et B distantes de 10 cm, percées chacune d’un trou en leur centre, et aux bornes desquelles on applique une tension U = 10 kV. À la sortie de la zone d’accélération, les agrégats entrent dans une zone de déplacement libre où règne un vide poussé. On enregistre alors le temps de vol des agrégats, c’est-à-dire la durée pour parcourir la distance D entre la plaque B et le détecteur.
La mesure du temps de vol permet de déterminer la masse m de l’agrégat.
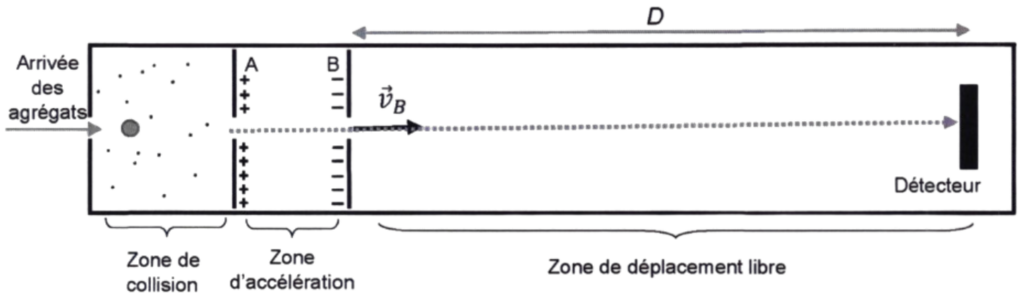
Figure 1 – Dispositif simplifié de l’accélérateur linéaire
Données
- Charge d’un agrégat : q = + 1,60 x 10‒19 C
- Tension entre les plaques A et B : UAB = U = 10,0 kV
- Distance entre les plaques : AB = 10 cm
- Nombre d’Avogadro : NA= 6, 02 x 1023 mol‒1
- Masse molaire de l’eau : M = 18,0 g·mol‒1
- Intensité de la pesanteur : g = 9,81 m·s‒2
Rappel
Pour un condensateur plan présentant une distance AB entre ses armatures, le champ électrique entre les deux armatures est uniforme et est relié à la tension UAB par la relation : $$ E=\frac{\left|U_{AB}\right|}{AB} $$
1. Montrer que la masse m1 d’un agrégat contenant N = 50 molécules d’eau est d’environ 1,50×10-24 kg et expliquer pourquoi il n’est pas possible de déterminer cette masse directement.
$$n=\frac{m_1}{M}$$
$$\frac{m_1}{M}=n$$
$$m_1=n\times M$$
Or
$$n=\frac{N}{N_A}$$
$$m_1=\frac{N}{N_A}\times M$$
$$m_1=\frac{50}{6,02\times {10}^{23}}\times 18,0$$
$$m_1=1,50\times {10}^{-21}\ g$$
$$m_1=1,50\times {10}^{-24}\ kg$$
2. Sur un schéma, représenter le vecteur champ électrique $ \overrightarrow{E} $ dans la zone d’accélération et déterminer sa valeur E.
$\overrightarrow{E}$ :
Direction : perpendiculaire aux plaques
Sens : de la plaque positive vers la plaque négative
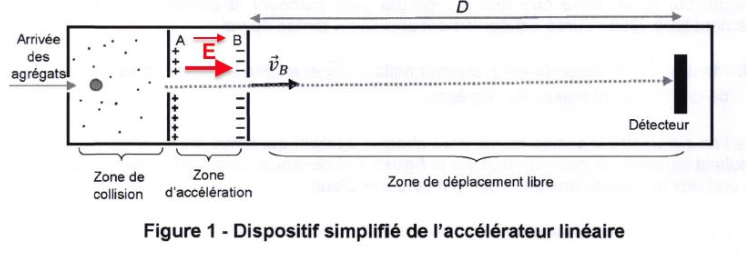
$$E=\frac{\left|U_{AB}\right|}{AB}$$
$$E=\frac{\left|10,0\times 10^3\right|}{10\times {10}^{-2}}$$
$$E=1,0\times {10}^5\ V.m^{-1}$$
3. Donner les caractéristiques (direction, sens, valeur) de la force électrique $ \overrightarrow{F} $ qui s’exerce sur un agrégat dans la zone d’accélération.
$$\overrightarrow{F}=q\overrightarrow{E}$$
Or la charge d’un agrégat est : $q=+1,6\times {10}^{-19}\ C$
Donc $\overrightarrow{F}$ et $\overrightarrow{E}$ ont le même sens et la même direction.
$\overrightarrow{F}$ :
Direction : perpendiculaire aux plaques
Sens : de la plaque positive vers la plaque négative
4. Montrer, en comparant les valeurs P1 du poids d’un agrégat de masse m1 et F de la force électrique, qu’il est possible de négliger l’effet du poids devant celui de la force électrique.
$$F=q\times E$$
$$F=1,60\times {10}^{-19}\times 1,0\times {10}^5$$
$$F=1,60\times {10}^{-14}\ N$$
$$P=m_1\times g$$
$$P=1,50\times {10}^{-24}\times 9,81$$
$$P=1,47\times {10}^{-23}\ N$$
Comparons les deux forces :
$$\frac{F}{P}=\frac{1,60\times {10}^{-14}}{1,47\times {10}^{-23}}=1,09\times {10}^9$$
Ainsi, le poids est négligeable devant la force électrique.
5. Exprimer le travail $ W_{AB}(\overrightarrow{F}) $ de la force électrique dans la zone d’accélération en fonction de q et U.
$$W_{AB}\left(\overrightarrow{F}\right)=\overrightarrow{F}\cdot \overrightarrow{AB}$$
$$W_{AB}\left(\overrightarrow{F}\right)=q\times \overrightarrow{E}\cdot \overrightarrow{AB}$$
$$W_{AB}\left(\overrightarrow{F}\right)=q\times E\times AB\times \cos\left(\alpha\right)$$
$$W_{AB}\left(\overrightarrow{F}\right)=q\times E\times AB\times \cos\left(0\right)$$
$$W_{AB}\left(\overrightarrow{F}\right)=q\times E\times AB\times 1$$
$$W_{AB}\left(\overrightarrow{F}\right)=q\times E\times AB$$
$$W_{AB}\left(\overrightarrow{F}\right)=q\times \frac{U}{AB}\times AB$$
$$W_{AB}\left(\overrightarrow{F}\right)=q\times U$$
La vitesse vA d’un agrégat de masse m entrant dans la zone d’accélération est négligeable devant la vitesse de sortie vB.
6. En utilisant le théorème de l’énergie cinétique, montrer que la vitesse en sortie de zone d’accélération est donnée par $v_B=\sqrt{\frac{2qU}{m}}$.
Théorème de l’énergie cinétique : La variation d’énergie cinétique entre deux points O et S est égale a la somme des travaux des forces :
$$\Delta E_C=\Sigma W_{OS}\left(\overrightarrow{F}\right)$$
$$E_{C\ finale}-E_{C\ initiale}=W_{OS}\left(\overrightarrow{F}\right)$$
$$E_C\left(B\right)-E_C\left(A\right)=q\times U$$
$$\frac{1}{2}\times m\times v_B^2-\frac{1}{2}\times m\times v_A^2=q\times U$$
La vitesse $v_A$ d’un agrégat de masse $m$ entrant dans la zone d’accélération est négligeable devant la vitesse de sortie $v_B$.
$$\frac{1}{2}\times m\times v_B^2=q\times U$$
$$v_B^2=\frac{2\times q\times U}{m}$$
$$v_B=\sqrt{\frac{2\times q\times U}{m}}$$
7. En négligeant le poids de l’agrégat dans la zone de déplacement libre, décrire le mouvement de l’agrégat dans la zone de déplacement libre.
En négligeant le poids de l’agrégat dans la zone de déplacement libre, il n’y a pas de forces qui s’exercent sur l’agrégat dans la zone de déplacement libre.
D’après la première loi de Newton, lorsque $\Sigma\overrightarrow{F}=\overrightarrow{0}$, le mouvement est rectiligne uniforme.
On désigne par ∆t la durée qu’il faut à l’agrégat pour parcourir la distance D dans la zone de déplacement libre. Cette durée est également appelée « temps de vol ».
8. Montrer que la durée ∆t est proportionnelle à $\sqrt{m}$ et en déduire que la mesure de Δt permet de déterminer la masse de l’agrégat.
Lorsque le mouvement est rectiligne uniforme :
$$v=\frac{d}{\Delta t}$$
$$v\times \Delta t=d$$
$$\Delta t=\frac{d}{v}$$
Or $v=v_B$ car le mouvement est uniforme
$$\Delta t=\frac{d}{v_B}$$
Or
$$v_B=\sqrt{\frac{2\times q\times U}{m}}$$
$$\Delta t=d\times \sqrt{\frac{m}{2\times q\times U}}$$
La durée $\Delta t$ est donc proportionnelle à $\sqrt{m}$.
La mesure de $\Delta t$ étant reliée à $\sqrt{m}$, elle permet de déterminer la masse de l’agrégat.
Lorsque l’on enregistre le temps de vol pour chaque agrégat qui arrive sur le détecteur, on obtient des résultats similaires à ceux donnés sur la figure 2 ci-dessous. Le pic principal, dit de référence, correspond aux agrégats constitués de 50 molécules d’eau.
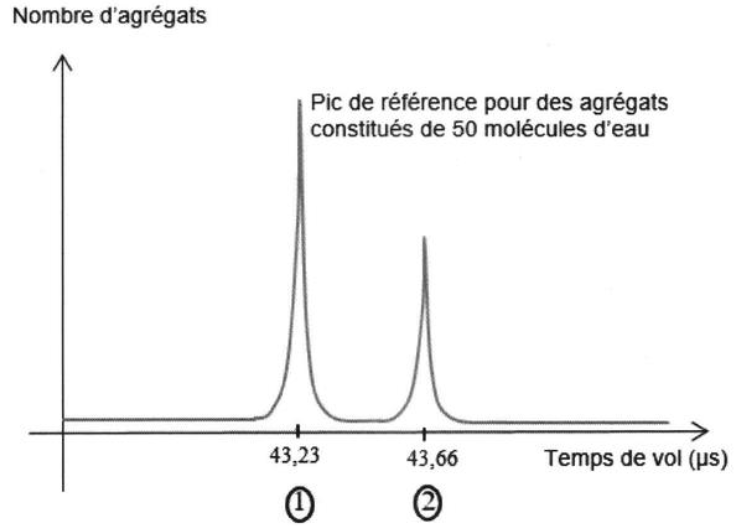
Figure 2 – Temps de vol des agrégats
9. Déterminer le nombre de molécules d’eau qui constituent les agrégats du deuxième pic.
$$\Delta t_1=d\times \sqrt{\frac{m_1}{2\times q\times U}}$$
$$\Delta t_2=d\times \sqrt{\frac{m_2}{2\times q\times U}}$$
Faisons le rapport :
$$\frac{\Delta t_2}{\Delta t_1}=\sqrt{\frac{m_2}{m_1}}$$
Méthode 2 : la question 8. nous indique que La durée $\Delta t$ est donc proportionnelle à $\sqrt{m}$ soit
$$\Delta t=k\times \sqrt{m}$$
$$\frac{\Delta t_2}{\Delta t_1}=\sqrt{\frac{m_2}{m_1}}$$
Isolons $m_2$ :
$$\sqrt{\frac{m_2}{m_1}}=\frac{\Delta t_2}{\Delta t_1}$$
$$\frac{m_2}{m_1}=\left(\frac{\Delta t_2}{\Delta t_1}\right)^2$$
$$m_2=m_1\times \left(\frac{\Delta t_2}{\Delta t_1}\right)^2$$
$$m_2=1,50\times {10}^{-24}\times \left(\frac{43,66}{43,23}\right)^2$$
$$m_2=1,53\times {10}^{-24}\ kg$$
$$m_2=1,53\times {10}^{-21}\ g$$
Méthode 3 : la question 8. nous indique que La durée $\Delta t$ est donc proportionnelle à $\sqrt{m}$ soit
| 43,23 | $\sqrt{1,50\times {10}^{-21}}$ |
| 43,66 | $\sqrt{m_2}$ |
$$\sqrt{m_2}=\frac{43,66\times \sqrt{1,50\times {10}^{-21}}}{43,23}$$
$$m_2=\left(\frac{43,66\times \sqrt{1,50\times {10}^{-21}}}{43,23}\right)^2$$
$$m_2=1,53\times {10}^{-21}\ g$$
Or (question 1)
$$m_2=\frac{N_2}{N_A}\times M$$
$$\frac{N_2}{N_A}\times M=m_2$$
$$N_2=\frac{m_2\times N_A}{M}$$
$$N_2=\frac{1,53\times {10}^{-21}\times 6,02\times {10}^{23}}{18,0}$$
$$N_2=51$$
51 molécules d’eau constituent les agrégats du deuxième pic.
