L’observation de Saturne

Bac Nouvelle Calédonie 2023 Sujet 1

Exercice 2 – (5 points) –  Durée 0h53 – Calculatrice autorisée

Sujet n°23-PYCJ1NC1

Sujet et corrigé

EXERCICE II – L’OBSERVATION DE SATURNE (5 points)

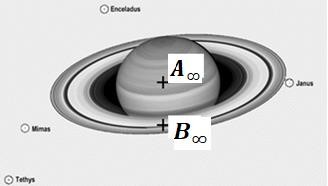
Figure 1: Image de Saturne depuis le télescope spatial Hubble© Nasa, ESA, photo prise le 20 juin 2019, https://hubblesite.org

L’exercice proposé étudie la capacité de l’œil à profiter du « spectacle exceptionnel » que peut offrir l’observation de la planète Saturne à l’aide d’une lunette astronomique.

On repère sur la figure 1 deux points considérés comme infiniment éloignés de la Terre :

• le centre de la planète Saturne, noté A_∞ ;
• un point de l’anneau externe, noté B_∞.

Données :

• Distance 𝐴_∞𝐵_∞ = 1,1 × 10⁸ m.
• La longueur d’onde de la radiation la plus lumineuse diffusée par Saturne est λ = 705 nm.

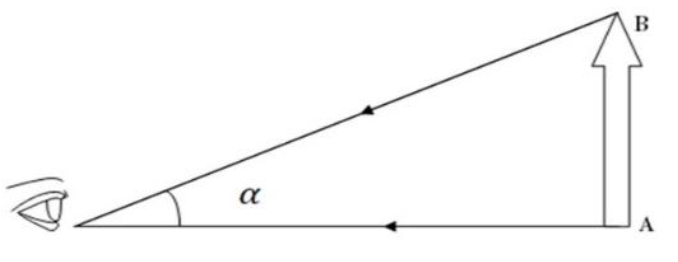
Figure 2

• L’angle apparent sous lequel le système d’anneaux de Saturne est vu depuis la Terre vaut α = 8 × 10⁻⁵ rad quand Saturne est au plus près de la Terre.
• Pour des petits angles exprimés en radians, on peut écrire tan 𝛼 ≈ 𝛼.
• Le pouvoir séparateur d’un instrument d’optique représente sa capacité à séparer deux points objets A et B très proches.

La limite de résolution angulaire d’un instrument d’optique est le plus petit angle apparent 𝛼_lim sous lequel sont observés deux points objets dont la lunette donne des images distinctes.

D’après le critère de Rayleigh, deux points objets sont séparés si 𝛼 (en radians) est supérieur à la limite de résolution 𝛼_lim, c’est-à-dire 𝛼 > 𝛼_lim= 1,22 × 𝜆/D où 𝐷 est le diamètre de l’objectif et l la longueur d’onde de la radiation émise avec le maximum d’intensité par les points objets observés.

Partie A – Limite de résolution d’une lunette astronomique et pouvoir séparateur de l’œil

La lunette astronomique et l’œil sont limités dans leur capacité à discerner deux points objets.

A.1. Déterminer s’il est possible ou non de profiter du « spectacle exceptionnel » que peut offrir l’observation de la planète Saturne avec ses anneaux à l’œil nu.

D’après les données : L’angle apparent sous lequel le système d’anneaux de Saturne est vu depuis la Terre vaut α = 8 × 10⁻⁵ rad quand Saturne est au plus près de la Terre.

Or, toujours d’après les données, On considère qu’un œil normal ne peut pas distinguer deux points objets A et B très proches si l’angle apparent sous lequel ils sont vus est inférieur à 2,9 × 10⁻⁴ rad.

α<2,9 × 10⁻⁴ rad : il n’est pas possible de profiter du « spectacle exceptionnel » que peut offrir l’observation de la planète Saturne avec ses anneaux à l’œil nu.

On observe Saturne avec une lunette astronomique dont un extrait de la notice technique est reproduit figure 3.

Diamètre de l’objectif (en mm)	70
Distance focale de l’objectif (en mm)	900
Mouvement lent	à friction
Monture	azimutale
Ouverture	70
Distances focales des oculaires	20 mm et 10 mm
Grossissement avec équipement livré	45 X et 90 X

Figure 3 : Extrait de la notice d’une lunette astronomique

A.2. À partir du critère de Rayleigh, déterminer la limite de résolution angulaire 𝛼_lim de cette lunette commerciale.

$$\alpha_{lim}=1,22\times\frac{\lambda}{D}$$
D’après les données : La longueur d’onde de la radiation la plus lumineuse diffusée par Saturne est $\lambda = 705\ \mathrm{nm}$.
$$\alpha_{lim}=1,22\times\frac{705\times{10}^{-9}}{70\times{10}^{-3}}$$
$$\alpha_{lim}=1,2\times{10}^{-5}\ \mathrm{rad}$$
La limite de résolution angulaire $\alpha_{lim}$ de cette lunette commerciale à pour valeur :
$$\alpha_{lim}=1,2\times{10}^{-5}\ \mathrm{rad}.$$

A.3. Indiquer si le phénomène ondulatoire limitant la résolution empêche ou pas l’observation de Saturne avec la lunette proposée.

$\alpha>\alpha_{lim}=1,2\times{10}^{-5}\ \mathrm{rad}$ : le phénomène ondulatoire limitant la résolution n’empêche pas l’observation de Saturne avec la lunette proposée.

Partie B – Formation de l’image de Saturne et de ses anneaux

Sur le schéma de l’ANNEXE II À RENDRE AVEC LA COPIE (page 13/13), on modélise la lunette astronomique à l’aide de deux lentilles minces convergentes L₁ et L₂, de centres optiques respectifs O₁ et O₂ et d’axe optique Δ.

La lunette afocale est réglée de façon à procurer les meilleures conditions d’observations. Elle donne d’un objet A_∞B_∞ , situé à l’infini, une image A’_∞B’_∞  située à l’infini, observable sans accommoder pour un œil normal.

La planète Saturne et ses anneaux, supposés à l’infini, sont représentés sans souci d’échelle par A_∞B_∞, le point A_∞ étant sur l’axe optique. Un rayon lumineux issu de B_∞ est également représenté.

B.1.1. Identifier sur le schéma de l’ANNEXE II À RENDRE AVEC LA COPIE (page 13/13), l’objectif L1 et l’oculaire L2.

L₁ : l’objectif car c’est la lentille placée vers l’objet

L₂ : l’oculaire car c’est une lentille convergente possédant une petite distance focale.  C’est la lentille où on place l’œil.

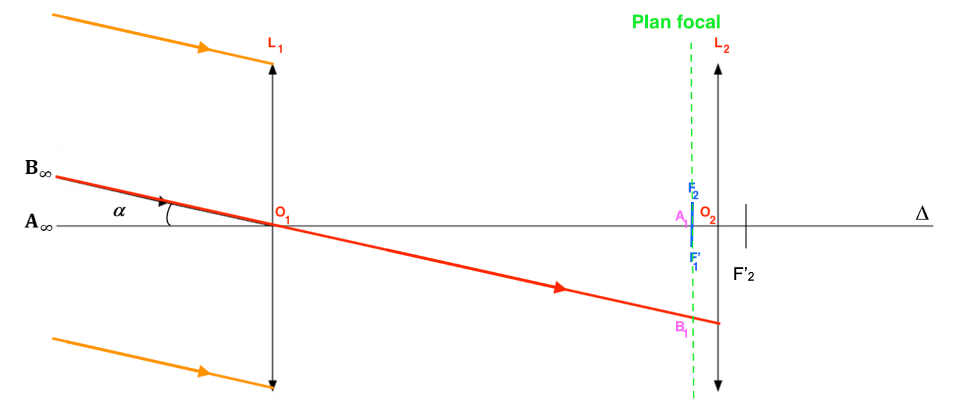
B.1.2. Positionner sur le schéma de l’ANNEXE II À RENDRE AVEC LA COPIE (page 13/13) :

• les centres optiques respectifs O₁ et O₂ ;
• le foyer image F’₁ de L₁ et le foyer objet F₂ de L₂ sans souci d’échelle mais de façon cohérente.

Les centres optiques respectifs O1 et O2 ; sont placés respectivement aux centres des lentilles L₁ et L₂.

Le foyer objet F₂ de L₂ :  O₂F₂= O₂F’₂

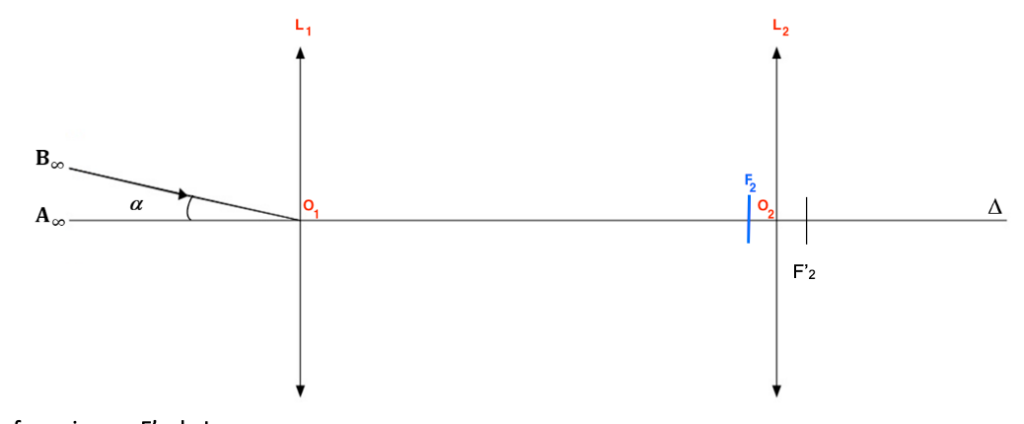
Le foyer image F’₁ de L₁ :

D’après le sujet la lunette est afocale. La lentille L₁, donne de l’objet A_∞B_∞, une image A₁B₁ sur le foyer image F’₁. Pour que L₂ donne une image A’_∞B’_∞, il faut que  soit sur le foyer objet F_2.

Ainsi, les deux foyers  F’₁ et F₂ sont confondus.

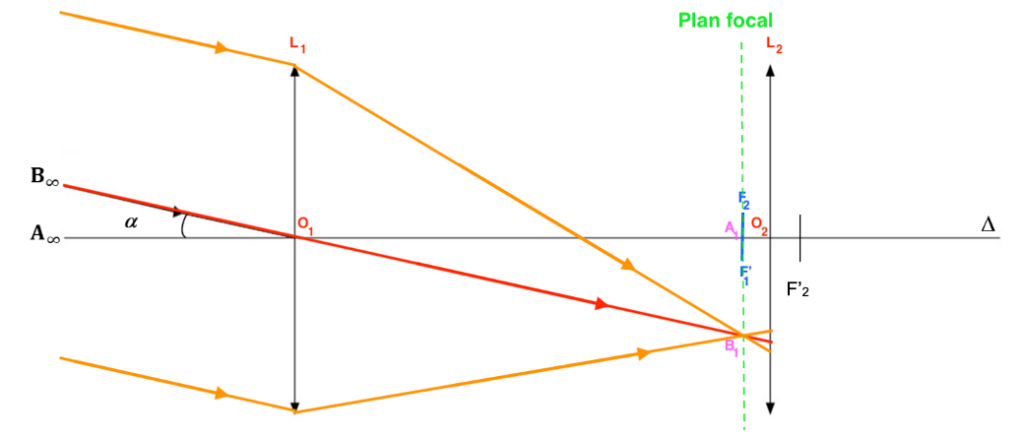
B.2. Représenter sur le schéma de l’ANNEXE II À RENDRE AVEC LA COPIE (page 13/13) :

• l’image intermédiaire A₁B₁ de l’objet A_∞B_∞ donnée par l’objectif L₁ ;
• le faisceau émergent de la lunette issu de B_∞ et passant par les bords de l’objectif.

La lentille L₁, donne de l’objet A_∞B_∞, une image A₁B₁ sur le plan focal.

Le rayon issu de B, passant par O₁ n’est pas dévié.

Le point B₁ est défini par l’intersection de ce rayon et le plan focal.

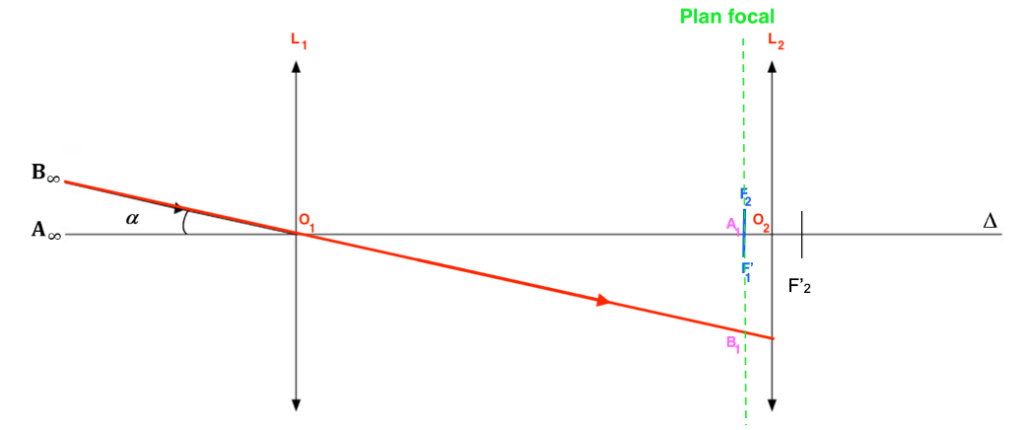
Le faisceau émergent de la lunette issu de B_∞ et passant par les bords de l’objectif :

Tous les rayons issus de B sont parallèles entre eux car ils proviennent de l’infini.

Tous les rayons issus de B se rejoignent au point B₁.

Partie C – Grossissement de la lunette astronomique

Le grossissement de la lunette est donné par l’expression : $G=\frac{\alpha’}{\alpha}$, 𝛼′ étant l’angle sous lequel on voit l’image A’_∞B’_∞ de l’objet A_∞B_∞ à travers l’instrument.

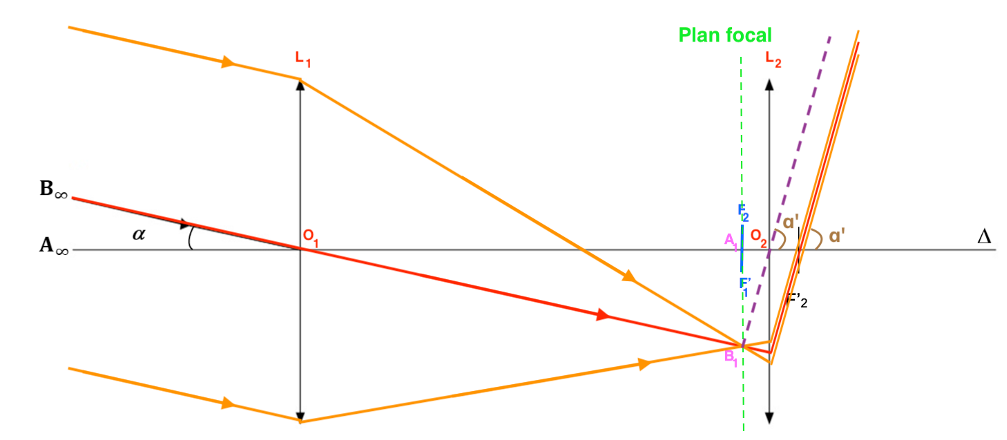
C.1. Repérer 𝛼′ sur le schéma de l’ANNEXE II À RENDRE AVEC LA COPIE (page 13/13).

Un rayon issu de B₁ passant par O₂ n’est pas dévié.

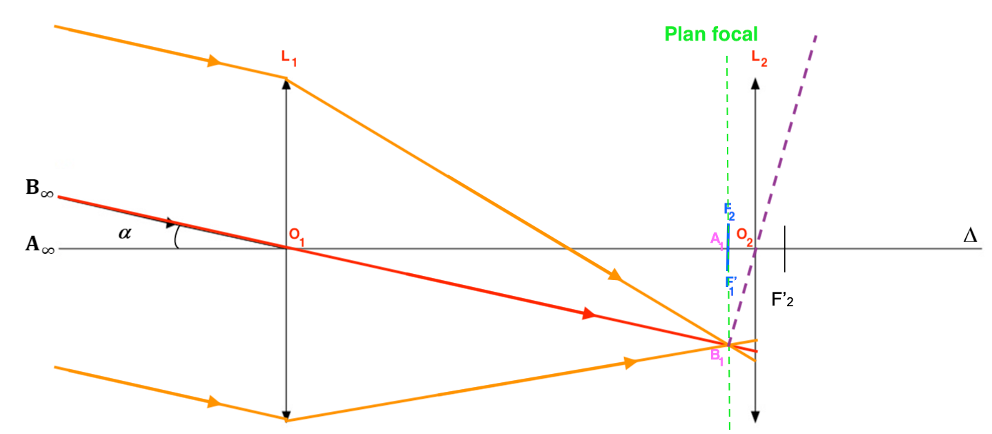
A₁B₁ étant sur le plan focal, il donnera une image à l’infini, tous les rayons issus de B₁, passant par la lentille L₂ seront parallèles.

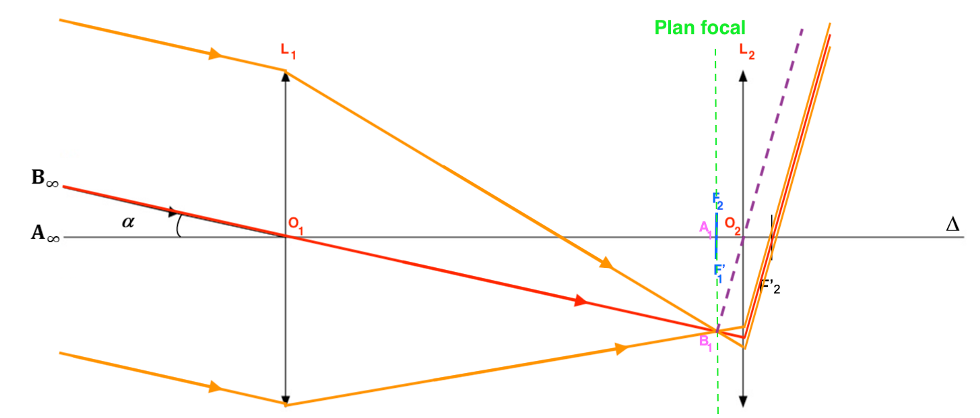
Remarque : L’échelle du schéma ne permet pas de bien voir les rayons au niveau du foyer image. Les rayons ne passent pas par F’₂.

$\alpha’$ est l’angle sous lequel est vue l’image finale en sortie de lunette.

C.2. Établir l’expression du grossissement 𝐺 en fonction des distances focales 𝑓₁^′ de l’objectif et 𝑓₂^′ de l’oculaire.

Le grossissement G est défini par :
$$G=\frac{\alpha’}{\alpha}$$

$$\tan\left(\alpha\right)\approx\alpha=\frac{A_1B_1}{f’_1}$$
$$\tan\left(\alpha’\right)\approx\alpha’=\frac{A_1B_1}{f’_2}$$

$$G=\frac{\alpha’}{\alpha}=\frac{\frac{A_1B_1}{f’_2}}{\frac{A_1B_1}{f’_1}}=\frac{A_1B_1}{f’_2}\times\frac{f’_1}{A_1B_1}=\frac{f’_1}{f’_2}$$

L’observateur utilise l’oculaire de distance focale 20 mm.

C.3. Valider la valeur du grossissement « 45 X » de la lunette commerciale décrite en figure 3.

$$G=\frac{f’_1}{f’_2}$$
$$G=\frac{900\times{10}^{-3}}{20\times{10}^{-3}}$$
$$G=45$$
La valeur du grossissement « 45 X » de la lunette commerciale décrite en figure 3 est validée.

C.4. Déterminer si l’œil peut théoriquement discerner les anneaux de Saturne avec l’aide de cette lunette.

Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée.

$$G=\frac{\alpha’}{\alpha}$$
$$\frac{\alpha’}{\alpha}=G$$
$$\alpha’=G\times\alpha$$
$$\alpha’=45\times8\times{10}^{-5}\ $$
$$\alpha’=3,6\times{10}^{-3}\ \mathrm{rad}\ $$

D’après les données :
D’après les données, On considère qu’un œil normal ne peut pas distinguer deux points objets A et B très proches si l’angle apparent sous lequel ils sont vus est inférieur à $2,9 \times 10^{-4}\ \mathrm{rad}$.
$$\alpha’=3,6\times{10}^{-3}\ \mathrm{rad} > 2,9 \times 10^{-4}\ \mathrm{rad}$$ : l’œil peut théoriquement discerner les anneaux de Saturne avec l’aide de cette lunette.

ANNEXE II À RENDRE AVEC LA COPIE (même non complétée)

EXERCICE II

Modélisation de la lunette astronomique