Enseignement scientifique Terminale
Durée 1h – 10 points – Thème « Une histoire du vivant »
Cet exercice a pour objet l’étude démographique d’une population.
Document 1 : effectifs de la population en Afrique du Sud depuis 1950
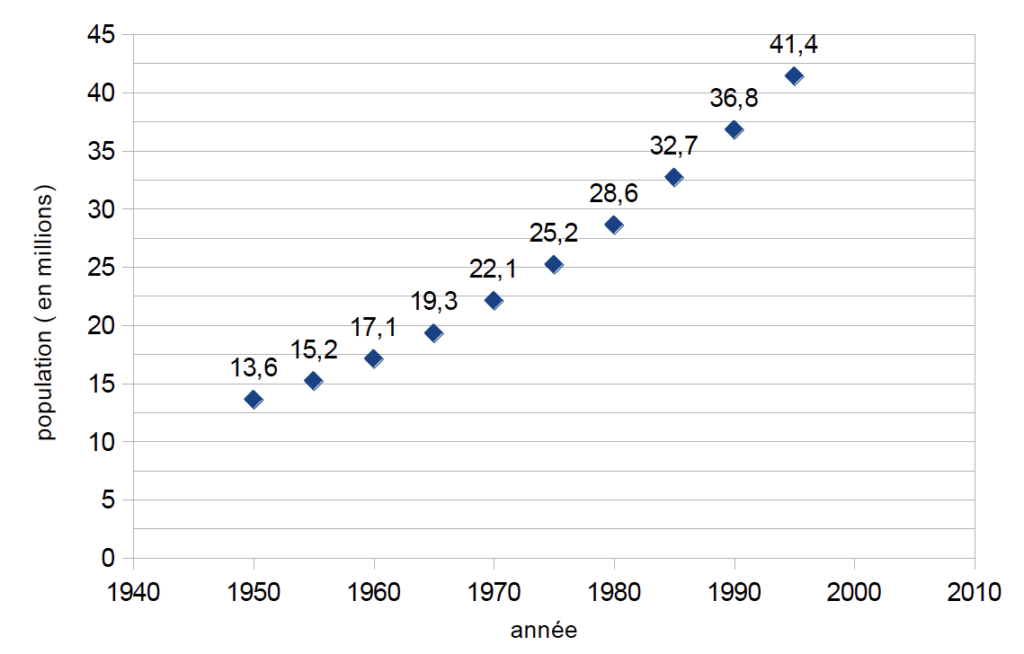
D’après World population prospects
Document 2 : données démographiques d’Afrique du Sud
| Année | Taux de natalité (pour mille) | Taux de mortalité (pour mille) | Taux d’accroissement annuel moyen (pour cent) |
| 1950 | 43,3 | 20,3 | 2,3 |
| 1960 | 41,6 | 16,7 | 2,5 |
| 1970 | 37,1 | 13,1 | 2,4 |
| 1980 | 33,9 | 10,2 | 2,4 |
| 1990 | 28,3 | 8,1 | 2 |
| 2000 | 22,6 | 16,9 | 0,6 |
Document 3 :la démographie dans différents pays d’Afrique sub-saharienne
Depuis 1990, l’Afrique sub-saharienne, globalement, est entrée dans une phase de ralentissement démographique, passant de 2,9 % de croissance par an vers 1985 à 2,3 % en 2000.
Mais ce ralentissement se fait à des rythmes variables, et même divergents entre les pays.À un extrême, on trouve une petite vingtaine de pays, de différentes sous-régions, dont les croissances n’ont pas changé ou même ont légèrement augmenté depuis 1985 (le Niger, le Mali, le Mozambique, la Somalie, etc.) ; à l’autre extrême, les cinq pays d’Afrique australe, le Zimbabwe et la Zambie dont les taux de croissance s’effondrent littéralement à partir de 1995 avec la surmortalité due au SIDA[…]: l’Afrique du Sud et le Botswana par exemple passent respectivement d’une croissance de 2,0 % et 2,8 % en 1990-1994 à 0,6 % et 0,9 % dix ans plus tard. C’est un exemple unique dans l’histoire.
Source : D’après « la démographie de l’Afrique au sud du Sahara des années 1950 aux années 2000 »
Population, 2004, www.cairn-int.info/revue-population-2004-3-page-521.htm
En 1950, l’Afrique du Sud est peuplée de 13,6 millions d’habitants. Entre 1950 et 1990, on a constaté que la population sud-africaine a augmenté en moyenne, d’une année sur l’autre, de 2,5%.
On modélise la population sud-africaine à l’aide d’une suite u. On note u(0) le nombre d’habitants en Afrique du Sud en 1950 et u(n) la population d’Afrique du Sud n années après 1950. Ainsi u(1) est le nombre d’habitants en 1951.
1- Justifier que l’on a la relation : u(n+1) = 1,025×u(n) pour n entier naturel.
D’après le sujet « Entre 1950 et 1990, on a constaté que la population sud-africaine a augmenté en moyenne, d’une année sur l’autre, de 2,5%. »
L’année d’après n+1 : la population u(n+1) est celle de l’année dernière (année n , population u(n)) avec une augmentation de 2,5% :
u(n+1)= u(n)+2,5/100 u(n)
u(n+1)= u(n)+0,025 u(n)
u(n+1)=1,025 u(n)
2- Vérifier qu’à l’aide de ce modèle, la population sud-africaine en 1951 est estimée à environ 13,9 millions d’habitants.
D’après le sujet « En 1950, l’Afrique du Sud est peuplée de 13,6 millions d’habitants »
En utilisant la relation précédente :
u(n+1)=1,025 u(n)
u(1)=1,025 u(0)
u(1)=1,025 ×13,6
u(1)=13,9
Ainsi, à l’aide de ce modèle, la population sud-africaine en 1951 est estimée à environ 13,9 millions d’habitants.
3- À l’aide de ce modèle, estimer le nombre d’habitants en 1995 et comparer avec la valeur donnée sur le document 1. Indiquer si la modélisation de la variation de la population sud-africaine semble satisfaisante et justifier la réponse.
u(n+1)=1,025 u(n) est une suite géométrique de raison q=1,025 et de premier terme u(0).
Mathématiquement, cette suite peut s’écrire sous la forme :
u(n)=u(0)×qn
u(n)=13,6×1,025n
Estimons, à l’aide de ce modèle le nombre d’habitants en 1995.
Tout d’abord, trouvons n :
n=1995-1950=45
u(45)=13,6×1,02545
u(45)=41,3
à l’aide de ce modèle le nombre d’habitants en 1995 est estimé à 41,3 millions.
La valeur donnée sur le document 1 est 41,4 millions d’habitants en 1995.
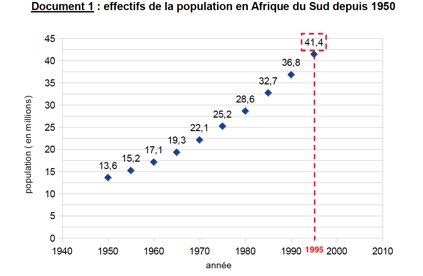
Ces deux valeurs sont très proches, la modélisation de la variation de la population sud-africaine semble donc satisfaisante.
4- Selon ce modèle, indiquer à partir de quelle année la population d’Afrique du sud dépassera 50 millions d’habitants.
Evaluons, selon ce modèle, à partir de quelle année la population d’Afrique du sud dépassera 50 millions d’habitants :
u(n)=13,6×1,025n
13,6×1,025n=u(n)
1,025n=u(n)/13,6
![\[ln(1,025^n)=ln(\frac{u(n)}{13,6}) \]](https://physik.fr/wp-content/ql-cache/quicklatex.com-75626595c92cd06c01674497c386f369_l3.png "Rendered by QuickLaTeX.com")
![\[n \times ln(1,025)=ln(\frac{u(n)}{13,6}) \]](https://physik.fr/wp-content/ql-cache/quicklatex.com-744ba04df32cd914cb60b250f06180ee_l3.png "Rendered by QuickLaTeX.com")
![\[n =\frac{ln(\frac{u(n)}{13,6})}{ln(1,025)} \]](https://physik.fr/wp-content/ql-cache/quicklatex.com-313a3cf9da6e2eb5ecff853ff744aa54_l3.png "Rendered by QuickLaTeX.com")
![\[n =\frac{ln(\frac{50}{13,6})}{ln(1,025)} \]](https://physik.fr/wp-content/ql-cache/quicklatex.com-ec393365d0265be1f19932a0026232c4_l3.png "Rendered by QuickLaTeX.com")
n=52,7
Or n est un nombre entier et nous cherchons quand cette population dépassera : n=53
n=année-1950
année-1950=n
année=n+1950
année=53+1950
année=2003
Selon ce modèle, la population d’Afrique du sud dépassera 50 millions d’habitants en 2003.
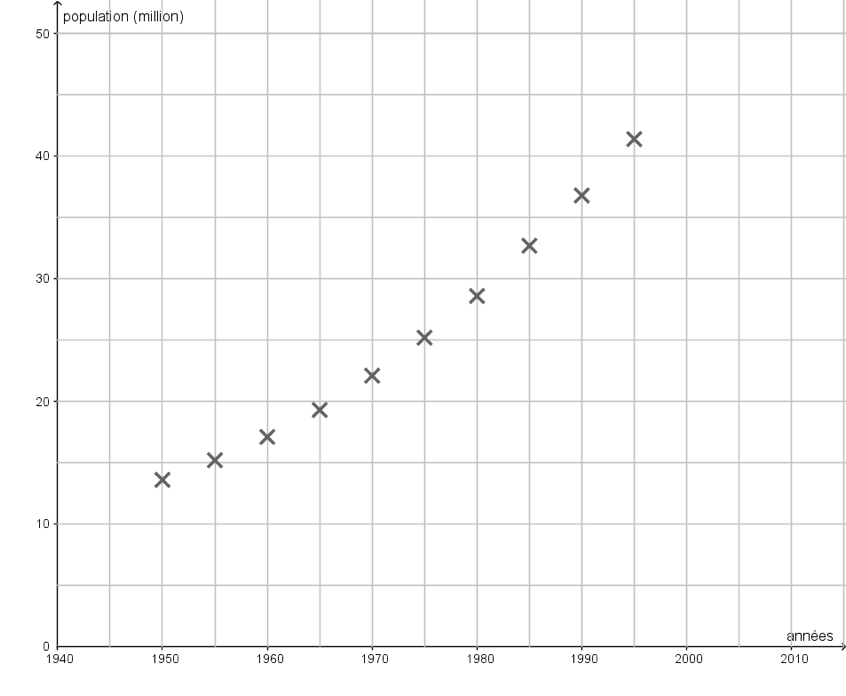
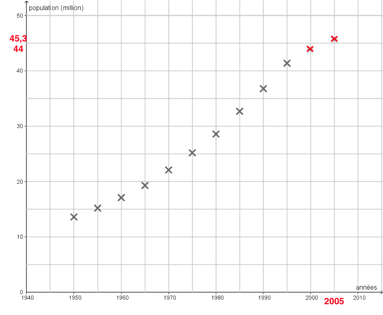
5- La population d’Afrique du Sud comptait respectivement 44 millions d’habitants en 2000 et 45,3 millions en 2005. Compléter avec ces données le graphique fourni en annexe (à rendre avec la copie). Indiquer si ces données sont conformes au modèle proposé. Justifier la réponse.
Estimons, à l’aide de ce modèle le nombre d’habitants en 2000.
Tout d’abord, trouvons n :
n=2000-1950=50
u(50)=13,6×1,02550
u(50)=46,7
à l’aide de ce modèle le nombre d’habitants en 2000 est estimé à 46,7 millions.
La valeur réelle 44 millions et la valeur du modèle 46,7 millions ne sont pas proches, la modélisation de la variation de la population sud-africaine n’est pas satisfaisante.
Estimons, à l’aide de ce modèle le nombre d’habitants en 2005.
Tout d’abord, trouvons n :
n=2005-1950=55
u(55)=13,6×1,02555
u(55)=52,9
à l’aide de ce modèle le nombre d’habitants en 2000 est estimé à 52,9 millions.
La valeur réelle 45,3 millions et la valeur du modèle 52,9 millions ne sont pas proches, la modélisation de la variation de la population sud-africaine n’est pas satisfaisante.
Ainsi, ces données ne sont pas conformes au modèle proposé.
6- En utilisant le document 2, justifier que le taux d’accroissement annuel moyen en 1970 est de 2,4 %.
Le taux d’accroissement annuel moyen est la différence entre le taux de natalité et le taux de mortalité :
| Année | Taux de natalité (pour mille) | Taux de mortalité (pour mille) | Taux d’accroissement annuel moyen (pour cent) |
| 1950 | 43,3 | 20,3 | 2,3 |
| 1960 | 41,6 | 16,7 | 2,5 |
| 1970 | 37,1 | 13,1 | 2,4 |
| 1980 | 33,9 | 10,2 | 2,4 |
| 1990 | 28,3 | 8,1 | 2 |
| 2000 | 22,6 | 16,9 | 0,6 |
Calculons le taux d’accroissement annuel moyen en 1970 :
taux d’accroissement annuel =Taux de natalité-Taux de mortalité
taux d’accroissement annuel =37,1-13,1
taux d’accroissement annuel =24 pour mille
taux d’accroissement annuel =2,4 pour cent
Le taux d’accroissement annuel moyen en 1970 est de 2,4 %.
7- Au regard du document 2, on émet l’hypothèse qu’à partir de 1950, le taux de mortalité de la population diminue de 3 points sur mille tous les 10 ans. Calculer les taux de mortalité attendus en 1990 et 2000. Les comparer aux valeurs réelles.
| Année | Taux de natalité (pour mille) | Taux de mortalité (pour mille) | Taux d’accroissement annuel moyen (pour cent) |
| 1950 | 43,3 | 20,3 | 2,3 |
| 1960 | 41,6 | 16,7 | 2,5 |
| 1970 | 37,1 | 13,1 | 2,4 |
| 1980 | 33,9 | 10,2 | 2,4 |
| 1990 | 28,3 | 8,1 | 2 |
| 2000 | 22,6 | 16,9 | 0,6 |
On émet l’hypothèse qu’à partir de 1950, le taux de mortalité de la population diminue de 3 points sur mille tous les 10 ans.
Prenons n le nombre de dizaine d’année :
Taux de mortalité (1950+n)=Taux de mortalité (1950)-3n
Calculons les taux de mortalité attendus en 1990 :
Taux de mortalité (1990)=Taux de mortalité (1950)-3×4
Taux de mortalité (1990)=20,3-3×4
Taux de mortalité (1990)=8,3
La valeur donnée sur le document 2 est un taux de mortalité de 8,1. Ces deux valeurs sont très proches, la modélisation semble donc satisfaisante.
Calculons les taux de mortalité attendus en 2000 :
Taux de mortalité (2000)=Taux de mortalité (1950)-3×5
Taux de mortalité (2000)=20,3-3×5 T
aux de mortalité (2000)=5,3
La valeur donnée sur le document 2 est un taux de mortalité de 16,9. Ces deux valeurs ne sont pas proches, la modélisation n’est donc pas satisfaisante.
8- À partir de 1995, la population sud-africaine n’a plus suivi la variation prévue par ce dernier modèle. À l’aide des documents 2 et 3, donner des arguments permettant d’expliquer ce phénomène.
Arguments permettant d’expliquer ce phénomène :
- Le taux de mortalité a augmenté très fortement en 2000. Ainsi, la variation de la population sud-africaine n’a plus suivi la variation prévue par ce dernier modèle.
- Les taux de croissance s’effondrent littéralement à partir de 1995 avec la surmortalité due au SIDA
Annexe
Document réponse à rendre avec la copie
Réponse à la question 5
