E3C2 – 10 points – Durée 1h – calculatrice autorisée
Sujet n°G1SPHCH02788, n°G1SPHCH02791, n°G1SPHCH02802 et n°G1SPHCH02809
Télécharger l’exercice en PDF :
Le Soleil est la principale source du rayonnement électromagnétique reçu par la Terre. Une partie de ce rayonnement est constituée de radiations ultraviolettes (UV). Une exposition prolongée aux rayons ultraviolets peut provoquer des dommages au niveau des yeux ou de la peau, tels que brûlures, vieillissement prématuré ou cancers. Il est donc nécessaire de prendre certaines précautions pour s’en protéger.
1. Les différents types de rayons ultraviolets
Il existe trois catégories de rayonnements ultraviolets, classés par domaines de longueur d’onde selon leurs effets biologiques et leur pouvoir de pénétration dans la peau :
- les UV-A : 320 nm < λ < 400 nm ;
- les UV-B : 280 nm < λ < 320 nm ;
- les UV-C : 100 nm < λ < 280 nm ;
Plus l’énergie d’un rayonnement UV est élevée, plus celui-ci sera dangereux pour la peau.
Données :
- constante de Planck : h = 6,63×10–34 J.s ;
- la valeur de la célérité de la lumière c dans le vide est supposée connue du candidat ;
- 1 eV = 1,60×10–19 J.
1.1. Calculer, en eV, la valeur de l’énergie E d’un photon de longueur d’onde λ = 280 nm dans le vide.
$$E=h\times \nu=\ h\times \frac{c}{\lambda}$$
$$E=\ 6,63{.10}^{-34}\times \frac{3,00{.10}^8}{280{.10}^{-9}}$$
$$E=7,10{.10}^{-19}\ J$$
$$E=\frac{7,10{.10}^{-19}\ }{1,60{.10}^{-19}\ }=4,44\ ev$$
1.2. Classer, en justifiant, les différents types d’UV par nocivité croissante.
Plus l’énergie d’un rayonnement UV est élevée, plus celui-ci sera dangereux pour la peau.
Or l’énergie est inversement proportionnelle à la longueur d’onde :
$$E=\ h\times \frac{c}{\lambda}$$
$$\lambda_{UV-C\ }<\lambda_{UV-B\ }<\lambda_{UV-A\ }$$
Donc
$$E_{UV-A\ }<E_{UV-B\ }<E_{UV-C}$$
Classement des différents types d’UV par nocivité croissante : UV-A, UV-B et UV-C.
2. L’ozone, l’écran solaire de la Terre
Avant d’atteindre la surface de la Terre, le rayonnement solaire subit des phénomènes d’absorption et de diffusion dans les couches de l’atmosphère, notamment en raison de la présence de dioxygène et d’ozone (O3).
L’ozone est particulièrement présent dans la stratosphère, couche située entre dix et cinquante kilomètres d’altitude.
La couche d’ozone atmosphérique absorbe totalement les rayonnements ultraviolets de fréquence comprise entre 11×1014 Hz et 30×1014 Hz.
2.1. Déterminer quelle catégorie d’ultraviolets ne parvient pas jusqu’à la surface terrestre.
« La couche d’ozone atmosphérique absorbe totalement les rayonnements ultraviolets de fréquence comprise entre 11×1014 Hz et 30×1014 Hz. »
${11.10}^{14}Hz<\nu<{30.10}^{14}Hz$
Or
$$\lambda=\ \frac{c}{\nu}$$
$$\lambda_1=\ \frac{3,00{.10}^8}{{11.10}^{14}}=2,72{.10}^{-7}=272\ nm$$
$$\lambda_2=\ \frac{3,00{.10}^8}{{30.10}^{14}}=1,00{.10}^{-7}=100\ nm$$
D’ou
$$100\ nm<\lambda<272\ nm$$
La couche d’ozone atmosphérique absorbe totalement les rayonnements ultraviolets de longueur d’onde comprise entre 100nm et 272 nm ce qui correspond aux UV-C.
Lorsque le rayonnement UV traverse la stratosphère, certains photons incidents possèdent une énergie suffisante pour être absorbés par l’ozone. La transformation (dissociation) qui en résulte est modélisée par la réaction (1) :
O3 + photon → O2 + O* (1)
La notation O* signifie que l’atome d’oxygène formé est dans un état excité.
2.2. Le diagramme énergétique simplifié ci-dessous présente les niveaux d’énergie mis en jeu avant et après dissociation de l’ozone modélisée par la réaction (1).
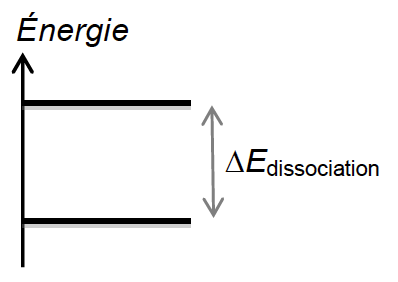
2.2.1. Recopier ce diagramme sur la copie et représenter par une flèche la transition correspondant au phénomène d’absorption des photons incidents par l’ozone.
Absorption= gain d’énergie. L’atome gagne de l’énergie, la flèche est dirigée vers le haut.
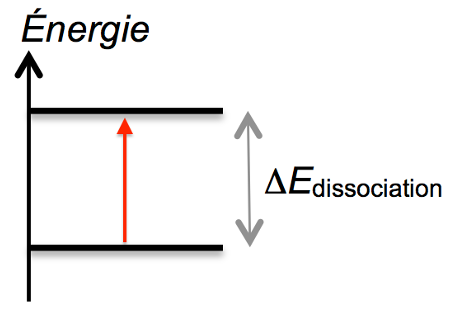
2.2.2. L’énergie de dissociation de l’ozone ΔEdissociation est égale à 4,97 eV. Montrer que cette valeur est en accord avec la réponse donnée à la question 2.1.
Calculons la longueur d’onde correspondant à ΔEdissociation
∆E=h×ν= h×c/λ
$$\lambda=\frac{h\times c}{\Delta E}$$
$$\lambda=6,63{.10}^{-34}\times \frac{3,00{.10}^8}{4,97\times 1,60{.10}^{-19}}$$
$$\lambda=2,50{.10}^{-7}m=250\ nm$$
Question 2.1 : « La couche d’ozone atmosphérique absorbe totalement les rayonnements ultraviolets de longueur d’onde comprise entre 100 nm et 272 nm ce qui correspond aux UV-C. »
Cette valeur est donc en accord avec la réponse donnée à la question 2.1. car comprise dans l’intervalle.
3. Le Soleil… sans coup de soleil
Pour limiter les effets des rayonnements UV sur la peau, il est recommandé par les dermatologues de porter des vêtements et accessoires protecteurs, et d’utiliser une crème solaire. Il existe deux grandes catégories de protection solaire offerte par les cosmétiques selon la nature des filtres et leur mode d’action ; tous doivent être expressément autorisés par la réglementation :
- les filtres organiques qui agissent par absorption des rayonnements UV ;
- les filtres minéraux, à savoir le dioxyde de titane (TiO2) et l’oxyde de zinc (ZnO), qui agissent par réflexion des rayons UV : ceux-ci ne pénètrent pas dans l’épiderme.
Ces différents filtres, chimiques ou minéraux […] peuvent être combinés entre eux par les fabricants […].
D’après https://www.economie.gouv.fr/dgccrf/Publications/Vie-pratique/Fiches-pratiques/Protection-solaire
Données :
- Spectre d’absorption de deux filtres minéraux, TiO2 et ZnO :
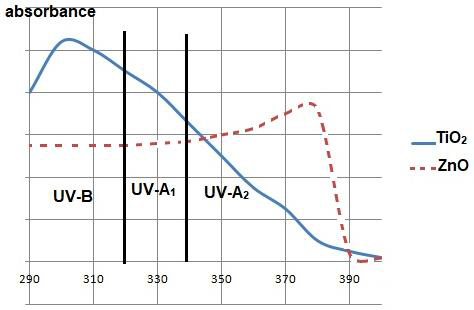
http://www.chimix.com/an19/bts/chim180.html
- L’avobenzone est un filtre organique dont la masse molaire M est égale à 310,4 g.mol-1.
- Spectre d’absorption de l’avobenzone :
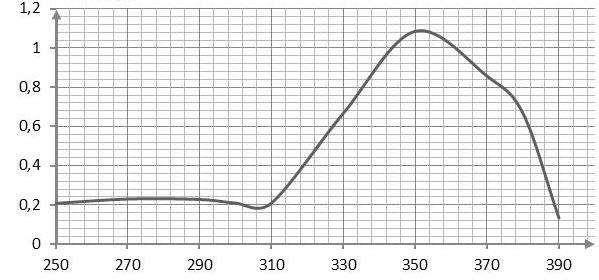
3.1. Expliquer l’intérêt pour un fabricant de crème solaire de combiner un filtre organique tel que l’avobenzone avec un filtre minéral tel que TiO2.
L’avobenzone est un filtre organique qui absorbe les rayonnements de longueur d’onde comprissent entre 325 nm et 380 nm.
Le filtre minéral TiO2 absorbe les rayonnements de longueur d’onde comprissent entre 290 nm et 340 nm.
Ainsi en combinant les 2 ont obtient une protection pour des rayonnements de longueur d’onde comprissent entre 290 nm et 380 nm.
Une crème solaire, dont le seul principe actif est l’avobenzone, est étudiée au laboratoire afin de vérifier son efficacité dans le temps.
Sa formulation est à 3 %, ce qui signifie que le pourcentage en masse de principe actif est de 3,0 g d’avobenzone pour 100 g de crème.
On considère que la crème solaire reste efficace et peut être conservée tant que le pourcentage en masse du principe actif est supérieur à 2,5 %.La période de conservation maximale après ouverture d’un produit cosmétique est indiquée par un symbole représentant un pot ouvert sur lequel la durée est précisée : 6 M pour 6 mois, 12 M pour 12 mois, 24 M pour 24 mois, etc.
Exemple de logo figurant sur un produit
Pour vérifier l’efficacité dans le temps de la crème solaire, on réalise la mesure de l’absorbance A, pour un rayonnement de longueur d’onde égale à 360 nm, de différentes solutions de concentration en quantité de matière c connue d’avobenzone dans du méthanol. Les résultats obtenus permettent le tracé de la courbe ci-après.
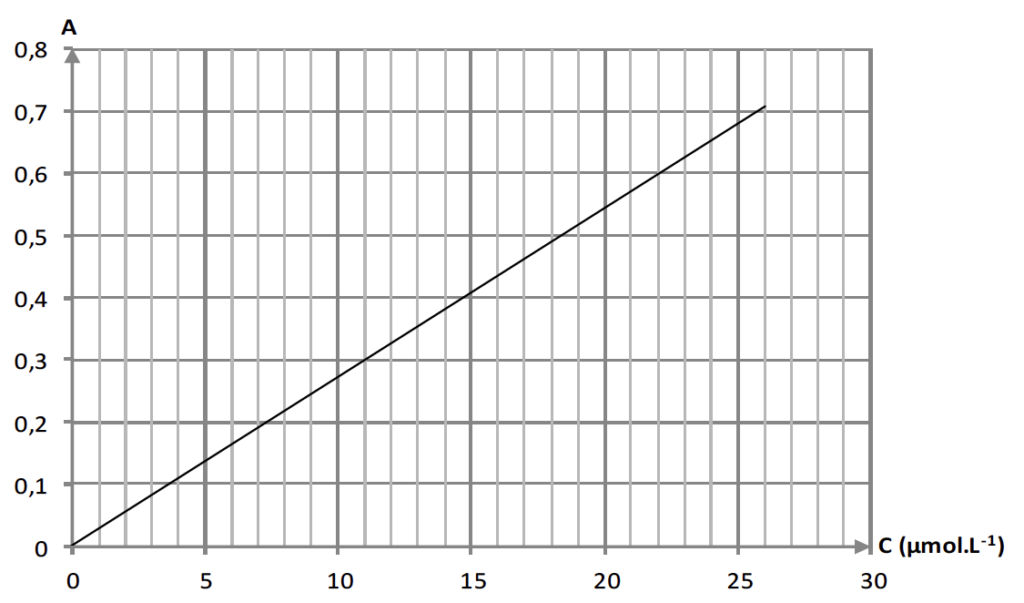
Tous les trois mois, on prépare une solution en introduisant 200 mg de crème solaire issue du même tube dans du méthanol pour obtenir un litre de solution dont on mesure l’absorbance.
Les résultats obtenus sont rassemblés dans le tableau suivant :
| Nombre de mois écoulés depuis l’ouverture du tube | 0 | 3 | 6 | 9 | 12 | 15 |
| Absorbance | 0,52 | 0,52 | 0,51 | 0,43 | 0,35 | 0,25 |
On considère que l’absorption des UV par des espèces chimiques autres que l’avobenzone est négligeable.
3.2. Justifier le choix de la longueur d’onde de travail.
« On réalise la mesure de l’absorbance A, pour un rayonnement de longueur d’onde égale à 360 nm »
On remarque, sur le graphe, que λ=360 nm est très proche de λmax, c’est pourquoi cette valeur est adaptée aux mesures.
3.3. Formulation de la crème solaire.
3.3.1. Déterminer la concentration en quantité de matière c0 de la solution réalisée à l’ouverture du tube de crème solaire.
A l’ouverture, A0=0,52.

Nous avons une droite passant par l’origine. La loi de Beer-Lambert est vérifiée.
La lecture graphique n’étant pas évidente, trouvons le coefficient directeur :
$$k=\frac{A_B-A_A}{C_B-C_B}$$
$$k=\frac{0,60-0}{22{.10}^{-6}-0}=2,7{.10}^4L{.mol}^{-1}$$
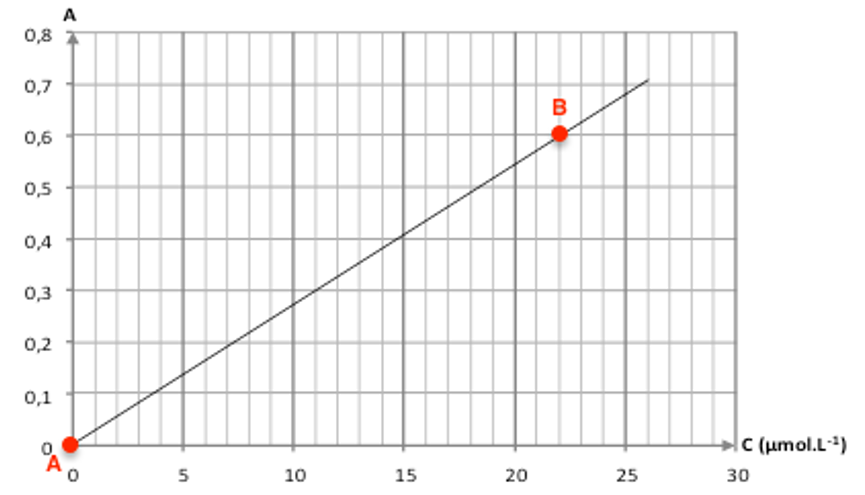
Calculons $C_0$ :
$$A=K\times C$$
$$A=2,7{.10}^4\times C$$
$$C=\frac{A}{2,7{.10}^4}$$
$$C_0=\frac{0,52\ }{2,7{.10}^4}=1,9{.10}^{-5}mol{.L}^{-1}$$
3.3.2. La formulation de la crème solaire est-elle bien celle attendue ?
« Sa formulation est à 3 %, ce qui signifie que le pourcentage en masse de principe actif est de 3,0 g d’avobenzone pour 100 g de crème »
Calculons la masse d’avobenzone contenu dans ce litre de solution qui provient de 200 mg de crème solaire :
$$n=\frac{m}{M}$$
$$m=n\times M$$
Or $$C=\frac{n}{V}$$
$$n=C\times V$$
D’ou
$$m=C\times V\times M$$
$$m=1,9{.10}^{-5}\times 1,0\times 310,4\ $$
$$m=5,9{.10}^{-3}\ g$$
Calculons le pourcentage en masse de principe actif :
$$P=\frac{m_{principe\ actif}}{m_{creme}}\times 100$$
$$P=\frac{5,9{.10}^{-3}\ }{200{.10}^{-3}\ }\times 100$$
$$P=3,0%$$
3.4. Évolution de la formulation de la crème solaire au cours du temps.
3.4.1. Indiquer, en justifiant, comment évolue la concentration en avobenzone au cours du temps.
| Nombre de mois écoulés depuis l’ouverture du tube | 0 | 3 | 6 | 9 | 12 | 15 |
| Absorbance | 0,52 | 0,52 | 0,51 | 0,43 | 0,35 | 0,25 |
Au cours du temps l’absorbance diminue. Or l’absorbance est proportionnelle à la concentration. Ainsi, la concentration en avobenzone diminue au cours du temps.
3.4.2. La mention «12 M » peut-elle être inscrite sur le logo figurant sur le tube de crème solaire ?
Le candidat est évalué sur ses capacités à concevoir et à mettre en œuvre une démarche de résolution, ainsi que sur la qualité de sa rédaction.
Toutes les prises d’initiative et toutes les tentatives de résolution, même partielles, seront valorisées.
« On considère que la crème solaire reste efficace et peut être conservée tant que le pourcentage en masse du principe actif est supérieur à 2,5 %. »
Calculons le pourcentage en masse du principe actif à 12 mois.
Pour cela déterminons la concentration (formule de la question 3.3.1) :
A=2,7{.10}^4\times C
$$C=\frac{A}{2,7{.10}^4}$$
$$C=\frac{0,35}{2,7{.10}^4}=1,3{.10}^{-5}mol{.L}^{-1}$$
Déterminons la masse d’avobenzone contenu dans ce litre de solution qui provient de 200 mg de crème solaire (formule de la question 3.3.2) :
$$m=C\times V\times M$$
$$m=1,3{.10}^{-5}\times 1,0\times 310,4\ $$
$$m=4,0{.10}^{-3}\ g$$
Calculons le pourcentage en masse de principe actif (formule de la question 3.3.2):
$$P=\frac{m_{principe\ actif}}{m_{crème}}\times 100$$
$$P=\frac{4,0{.10}^{-3}\ }{200{.10}^{-3}\ }\times 100$$
$$P=2,0%$$
Le pourcentage en masse du principe actif est inferieur à 2,5 %. Ainsi, la mention «12 M » ne peut pas être inscrite sur le logo figurant sur le tube de crème solaire.
