E3C2 – 10 points – Durée 1h – calculatrice autorisée
Sujet n°G1SPHCH02728 , n°G1SPHCH02736 et n°G1SPHCH02747
Télécharger l’exercice en PDF :

Données :
- masse du système {Alan Eustace et son équipement} : m = 120 kg ;
- intensité de la pesanteur à la surface de la Terre : g = 9,8 N/kg ;
- on considère que le champ de pesanteur est uniforme entre 30 km et 42 km d’altitude, de norme : gA= 9,7 N/kg.
L’étude du saut d’Alan Eustace est conduite dans le référentiel terrestre. Alan Eustace et son équipement sont modélisés par un point matériel de masse m. La position d’Alan Eustace est repérée par son altitude z sur un axe vertical orienté vers le haut, l’origine étant au sol.Alan Eustace s’est laissé tomber à une date choisie comme origine des temps (t = 0 s) à partir d’un point A d’altitude zA = 41 148 m par rapport au sol.

1. Énergie potentielle de pesanteur du système
1.1. Champ de pesanteur au cours de la chute.
1.1.1. Quelle est l’origine de la variation observée entre les valeurs de g et gA ?
L’intensité de pesanteur est inversement proportionnelle au carré de la distance au centre de la terre.
zA> z0 c’est pourquoi gA< g.
1.1.2. Calculer l’écart relatif donné par $ \frac{g-g_A}{g} $ et exprimé en %. Conclure.
$$\frac{g-g_A}{g}=\frac{9,8\ -9,7\ }{9,8\ }=0,01=1%$$
L’écart entre gA et g est négligeable. On peut considérer que g ne varie pas entre le sol et le point A.
1.2. Travail du poids au cours du saut.
1.2.1. En considérant que le poids du système {Alan Eustace et son équipement} est constant, établir l’expression du travail du poids du système lors du déplacement d’Alan Eustace de A jusqu’au sol en fonction de m, g, et zA.
Le travail du poids entre A et B est :
$$W_{AB}(\vec{P})=\vec{P}\cdot\vec{AB}=P\times AB\times\cos(\alpha)$$
L’angle entre $\vec{P}$ et $\vec{AB}$ est $\alpha=0$, donc $\cos(\alpha)=1$.
$P=mg$
$AB=z_A-z_B=z_A$ car $z_B=0$
Donc :
$$W_{AB}(\vec{P})=mgz_A$$
1.2.2. Calculer la valeur de ce travail.
$$W_{AB}(\vec{P})=120\times9,8\times41148$$
$$W_{AB}(\vec{P})=4,8.10^7\ J$$
1.3. Énergie potentielle de pesanteur.
1.3.1. « Le poids est une force conservative » ; expliquer cette expression.
Une force est dite conservative si son travail entre deux points A et B ne dépend pas de la trajectoire suivie entre ces deux points.
Ainsi, le travail du poids ne dépend pas du chemin parcouru.
1.3.2. Définir l’énergie potentielle de pesanteur Ep du système et montrer que son expression est Ep = mgz si on choisit une altitude de référence à préciser.
On définit la variation d’énergie potentielle de pesanteur par l’opposé du travail de la force du poids :
$$\Delta E_{pp}=E_{pp}(B)-E_{pp}(A)=-W_{AB}(\vec{P})$$
$$E_{pp}(B)-E_{pp}(A)=-mg(z_A-z_B)$$
L’énergie potentielle de pesanteur d’un solide est : Epp=mgz+C
L’énergie potentielle est définie à une constance prés. Elle dépend de l’origine de l’axe z choisi. Cependant sa variation ne dépend pas de l’origine choisie.
En choisissant l’énergie potentielle nulle au niveau du sol on obtient : Epp=mgz
2. Modélisation de la première phase du mouvement par une chute libre
Alan Eustace atteint un point B, d’altitude zB, après 50 s de chute.
Durant cette phase du mouvement, l’hypothèse est faite que la seule force s’exerçant sur le système {Alan Eustace et son équipement} est le poids.
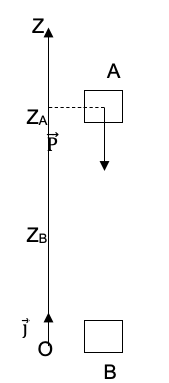
Dans ce cas, on peut montrer que la chute est verticale. Un logiciel de simulation permet d’obtenir la courbe donnant la valeur de la vitesse v d’Alan Eustace en fonction du temps t.
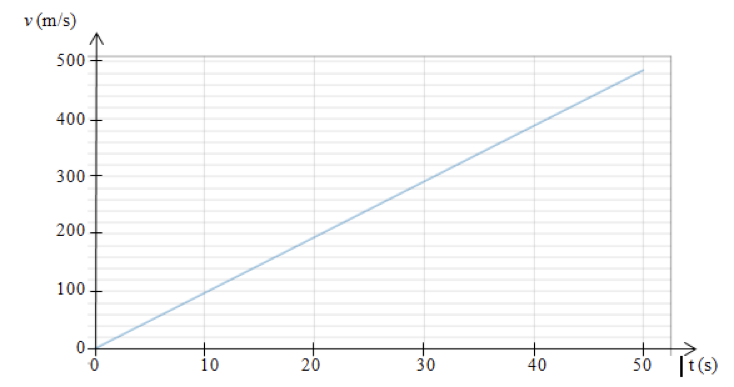
2.1. Montrer que ce modèle n’est pas compatible avec la donnée du texte introductif relative à la vitesse maximale atteinte.
D’après le texte :
« Après 50 s de chute, l’américain a atteint une vitesse maximale de 1322 km/h »
$$\frac{1322}{3,6}=367\ m.s^{-1}$$
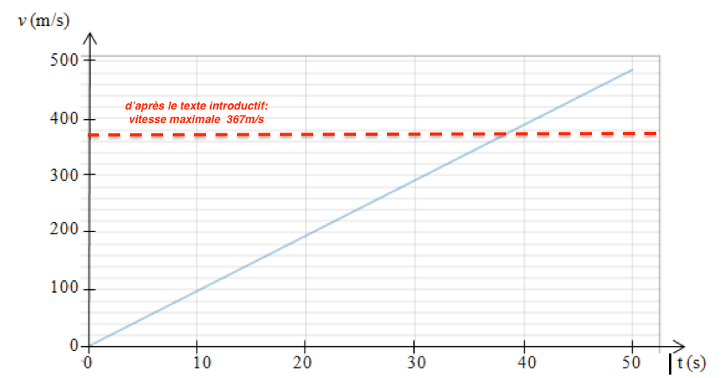
Le modèle n’est pas compatible avec la donnée expérimentale car il prévoit des vitesses supérieures.
2.2. Proposer une hypothèse expliquant l’écart entre valeur calculée et valeur expérimentale.
Avec ce modèle, au bout de 50 s :
$$v=485\ m.s^{-1}$$
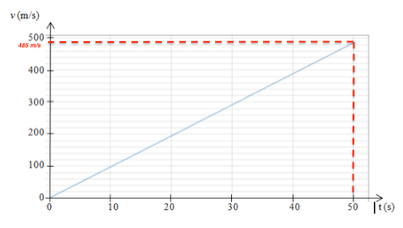
Le modèle considère une chute libre sans frottements, ce qui explique l’écart avec la valeur réelle.
3. Étude énergétique de la première phase du mouvement
On considère que la chute d’Alan Eustace durant les cinquante premières secondes est verticale.
L’action mécanique exercée par l’air sur Alan Eustace et son équipement est modélisée par une force de frottement fluide supposée constante.
L’altitude zB d’Alan Eustace après 50 s de chute est égale à 30 375 m.
3.1. Calcul de la valeur de la force de frottement fluide f dans le cadre de ce modèle.
3.1.1. Énoncer le théorème de l’énergie cinétique. Calculer la valeur de l’énergie cinétique à la fin de cette première phase.
Théorème de l’énergie cinétique :
$$\Delta E_c=\sum W_{AB}(\vec{F})$$
Énergie cinétique au point B :
$$E_c(B)=\frac{1}{2}mv_B^2$$
$$E_c(B)=\frac{1}{2}\times120\times367^2$$
$$E_c(B)=8,08.10^6\ J$$
3.1.2. Exploiter ce théorème et montrer que la valeur de la force de frottement est de l’ordre de 4.102 N.
$$E_c(B)-E_c(A)=W_{AB}(\vec{P})+W_{AB}(\vec{f})$$
$E_c(A)=0$
Le travail de la force de frottement :
$$W_{AB}(\vec{f})=f\times AB\times\cos(180)=-f(z_A-z_B)$$
Le travail du poids :
$$W_{AB}(\vec{P})=mg(z_A-z_B)$$
Donc :
$$E_c(B)=mg(z_A-z_B)-f(z_A-z_B)$$
$$f=\frac{E_c(B)-mg(z_A-z_B)}{-(z_A-z_B)}$$
$$f=\frac{8,08.10^6-120\times9,8\times(41148-30375)}{-(41148-30375)}$$
$$f=425\ N$$
La force de frottement est de l’ordre de $4.10^2\ N$.
3.1.3. Comparer la valeur obtenue au poids du système et conclure quant à la pertinence du modèle de la chute libre.
$$\frac{f}{P}=\frac{425}{120\times9,8}=0,36=36%$$
La force de frottement représente environ 35 % du poids : elle n’est pas négligeable. Le modèle de la chute libre n’est pas pertinent.
3.1.4. Discuter également de la pertinence de la modélisation de l’action de l’air par une force de frottement constante. On pourra s’interroger sur le lien entre la valeur de cette force et celle de la valeur de la vitesse d’Alan Eustace.
La force de frottement dépend de la vitesse. Lors de la chute, la vitesse n’est pas constante. Ainsi, contrairement à la modélisation, nous ne pouvons considérer que la force de frottement est constante.
3.2. L’extrait de programme donné ci-dessous et rédigé en langage Python, permet de visualiser les énergies cinétique, potentielle et mécanique du système {Alan Eustace + son équipement} durant la première phase du mouvement.
05. to, dt, tmax = 0, 1, 50
06. vo = 0
07. zo = 0 # ordonnée à t = 0 s, axe vertical orienté vers le haut
08.
09. z=zo
10. t=to
11. Eco=0 #énergie cinétique à to
12. Eppo=0 #énergie potentielle de pesanteur à to
13. Emo=0 #énergie mécanique à to
14.
15. g=9,7 #intensité de pesanteur en N/kg
16. m=120 #masse en kg
17.
18. ########## Création des listes ###########
19. tps=[0]
20. zlist= [z]
21. v=[0]
22. Eclist=[Eco]
23. Epplist=[Eppo]
24. Emlist=[Emo]
25.
26. while t<tmax :
27. t = t + dt
28. tps.append(t)
29.
30. v1 = vo + (-0.000044*vo*vo+9,7)*dt
31. vo=v1
32.
33. ########## Calculs de ###########
34. z=z-vo*dt #ordonnée à la date t
35. Ec=0.5*m*vo**2 #énergie cinétique à la date t
36. Epp=mgz #énergie potentielle de pesanteur à la date t
37. #Epp = 0 à t = 0 s
38. Em=Ec+Epp #énergie mécanique à la date t
3.2.1. À quelle ligne peut-on lire le choix de l’origine de l’axe vertical ici utilisée ?
À quelle position d’Alan Eustace correspond cette origine ?
Ligne 07. zo = 0 # ordonnée à t = 0 s, axe vertical orienté vers le haut
Cette origine correspond à la position initiale d’Alan Eustace.
3.2.2. En déduire que l’ordonnée d’Alan Eustace au cours du saut est négative pour ce choix d’origine.
Cet axe est orienté vers le haut. Au point de départ, zo = 0 . Alan Eustace chute donc z diminue. L’ordonnée d’Alan Eustace au cours du saut est donc négative pour ce choix d’origine.
3.2.3. Montrer que l’expression donnée à la ligne 36 est cohérente avec le commentaire de la ligne 37. Comment varie l’énergie potentielle de pesanteur au cours du saut ? Quel est son signe ?
En considérant le point de départ, zo = 0 , Epp(0)=mgzo = 0. c’est cohérent avec le commentaire de la ligne 37 (#Epp = 0 à t = 0 s).
Comme z décroit au cours de la chute Epp décroit car il est proportionnel à z.
Comme z est négatif au cours de la chute Epp est négatif car il est proportionnel à z.
