E3C2 – 10 points – Durée 1h – calculatrice autorisée
Sujet n°G1SPHCH02738
Télécharger l’exercice en PDF :
Le monde de la photographie évolue sans cesse. Après les appareils argentiques, utilisant des pellicules au format 24×36 mm, les appareils numériques ont fait leur apparition. Les dimensions du capteur utilisé dans ces appareils dépendent de la gamme de l’appareil.
Pour des appareils compacts, le format du capteur n’excède pas 6×8 mm. Pour les appareils dits « réflex », il peut aller jusqu’à 24×36 mm.
Principe de l’appareil réflex et modélisation de l’objectif
L’objectif de l’appareil, composé de plusieurs lentilles, est caractérisé par sa distance focale. Un miroir pivotant situé dans le boitier de l’appareil permet au photographe d’observer dans le viseur le sujet qu’il photographie. Le miroir pivotant se lève au moment de prendre le cliché : la lumière, après avoir traversé l’objectif, arrive alors directement sur le capteur.
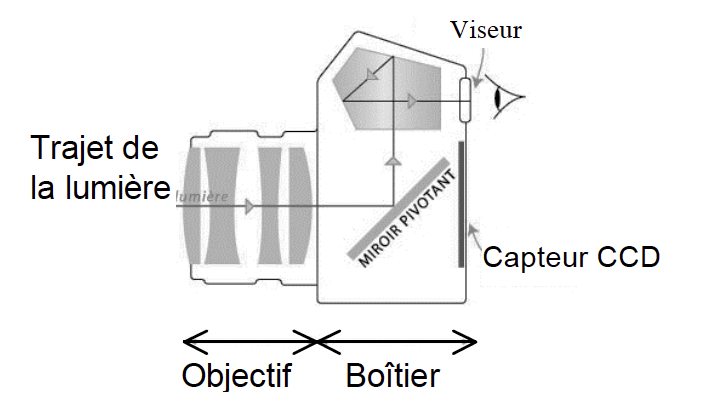
Pour simplifier, l’objectif peut être modélisé par une lentille mince convergente unique, dont la distance focale est égale à celle de l’objectif. Les distances sont donc exprimées par rapport au centre optique de cette lentille.
Quelques standards de capteurs pour appareils photographiques réflex
| Standard | Diagonale | Dimensions |
| Système micro 4/3 | 21,6 mm | 13×17,3 mm |
| APS-C | 24,8 mm | 15,8×23,6 mm |
| Plein format | 43,3 mm | 24×36 mm |
Données :
- relation de conjugaison :
$\frac{1}{\overline{OA’}}-\frac{1}{\overline{OA}}=\frac{1}{\overline{OF’}} $ ;
- grandissement : $\gamma=\frac{\overline{OA’}}{\overline{OA}}=\frac{\overline{A’B’}}{\overline{AB}} $ où O est le centre optique de la lentille, OF’ (ou f’) la distance focale de la lentille, AB l’objet et A’B’ l’image de cet objet obtenu avec la lentille mince.
1. Gros plan sur un martin pêcheur.
Un photographe dit avoir pris la photographie ci-contre, en milieu naturel, avec un objectif dont la distance focale peut varier de 28 mm à 100 mm. Il ne précise pas la distance focale utilisée pour cette image. L’oiseau était situé à 45 cm du centre optique de l’objectif et le capteur à 63 mm de ce centre optique.
La taille d’un martin pêcheur adulte est de l’ordre de 16 cm.

1.1. Distance focale de l’objectif.
1.1.1. Réaliser sur l’annexe à rendre avec la copie une construction graphique, à l’échelle ¼, pour déterminer la valeur de la distance focale de l’objectif lors de la prise de cette photo.
| Position oiseau (OA) | Position capteur (OA’) | Taille d’un martin pêcheur (AB) | |
| Dimensions réelles | 45 cm | 63 mm | 16 cm |
| échelle ¼ | 11,3 cm | 16 mm = 1,6cm | 4 cm |
Méthode :
- On place AB et A’B’
- On trace un rayon partant de B et passant par O, il n’est pas dévié
- On trace un rayon partant de B parallèle à l’axe optique, il est dévié et passe par B’
Or le rayon partant de B parallèle à l’axe optique est dévié en passant par F’. L’intersection entre ce rayon et l’axe optique est F’
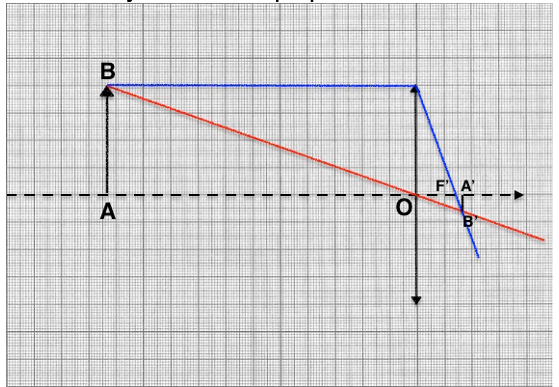
Sur le schéma, OF’ est situé à 1,4 cm soit 5,6 cm en dimensions réelles.
1.1.2. Retrouver cette valeur par un calcul.
$$\frac{1}{\overline{OA’}}=\frac{1}{\overline{OA}}+\frac{1}{\overline{OF’}}$$
$$\frac{1}{\overline{OF’}}=\frac{1}{\overline{OA’}}-\frac{1}{\overline{OA}}$$
$$\overline{OF’}=\frac{1}{\frac{1}{\overline{OA’}}-\frac{1}{\overline{OA}}}$$
$$\overline{OF’}=\frac{1}{\frac{1}{63.10^{-3}}-\frac{1}{-45.10^{-2}}}=5,5.10^{-2}\ m=5,5\ cm$$
1.2. Format du capteur.
1.2.1. Calculer le grandissement ɣ, puis la taille de l’image sur le capteur. Commenter les résultats obtenus et vérifier leur cohérence avec le schéma réalisé.
Grandissement :
$$\gamma=\frac{\overline{OA’}}{\overline{OA}}$$
$$\gamma=\frac{63.10^{-3}}{-45.10^{-2}}=-0,14$$
Taille de l’image sur le capteur :
$$\gamma=\frac{\overline{A’B’}}{\overline{AB}}$$
$$\overline{A’B’}=\gamma\times\overline{AB}$$
$$\overline{A’B’}=-0,14\times16.10^{-2}=-2,2.10^{-2}\ m$$
A’B’=2,2 cm
L’image est renversée (grandeur algébrique négative)
1.2.2. Quel(s) type(s) de capteur(s) le photographe a-t-il pu utiliser ? Justifier.
Capteurs disponibles :
| Standard | Diagonale | Dimensions |
| Système micro 4/3 | 21,6 mm | 13×17,3 mm |
| APS-C | 24,8 mm | 15,8×23,6 mm |
| Plein format | 43,3 mm | 24×36 mm |
A’B’=2,2 cm = 22 mm
Le photographe a pu utiliser seulement les capteurs APS-C ou Plein format compatibles avec la taille de l’image car de dimensions supérieures.
1.3. Exercer un regard critique sur les valeurs des distances précisées par le photographe dans cette situation.
Les valeurs des distances précisées par le photographe dans cette situation sont cohérentes avec les valeurs trouvées.
2. Restitution des couleurs.
L’écran d’un appareil photographique numérique permet d’observer la photographie obtenue. Les pixels de l’écran sont de trois types selon qu’ils émettent une lumière rouge (R), une lumière verte (V) ou une lumière bleue (B).
2.1. La couleur du plumage du ventre de l’oiseau ci-dessus peut être assimilée à du rouge.
2.1.1. Comment qualifie-t-on la lumière qui éclaire l’oiseau en milieu naturel ?
La lumière (blanche) qui éclaire l’oiseau en milieu naturel est polychromatique.
2.1.2. En utilisant le vocabulaire scientifique adapté, formuler une hypothèse expliquant pourquoi le plumage du ventre de l’oiseau apparaît rouge.
La lumière blanche est composée de rouge, vert et bleu.
Le plumage du ventre rouge absorbe le bleu et le vert et diffuse le rouge. Ainsi Le plumage du ventre apparait rouge.
2.2. Restitution des couleurs sur l’écran.
2.2.1. Comment nomme-t-on la synthèse des couleurs en jeu dans la restitution des couleurs sur l’écran de l’appareil photographique ?
La synthèse des couleurs en jeu dans la restitution des couleurs sur l’écran de l’appareil photographique est la synthèse additive.
2.2.2. Quel(s) est(sont) le(s) pixel(s) activé(s) dans la zone de l’image correspondant :
- au plumage des ailes, de couleur cyan ;
- à la pointe du bec qui est noire ;
- à la zone du cou qui est blanche.
| Zones | pixel(s) activé(s) |
| au plumage des ailes, de couleur cyan | Vert et bleu |
| à la pointe du bec qui est noire | Aucun |
| à la zone du cou qui est blanche | Rouge, vert et bleu |
3. Règle des tiers.
La photo ci-dessous a été prise avec un appareil muni d’un objectif de distance focale f’ égale à 50 mm. Elle respecte la règle des tiers, règle académique permettant de réussir nombre de cadrages. Cette règle consiste à placer les éléments forts de l’image sur les lignes horizontales et verticales placées au tiers de l’image, et aux points d’intersection entre ces lignes.

Données :
- Extrait des caractéristiques de l’appareil réflex numérique utilisé :
| Type | |
| Type | Appareil photo numérique de type réflex |
| Monture d’objectif | Monture à baïonnette avec couplage AF et contacts AF |
| Angle de champ | Équivalent à l’angle de la focale de l’objectif (1,5 fois lorsque le format DX est sélectionné) |
| Pixels effectifs | |
| Pixels effectifs | 12,1 millions |
| Capteur d’image | |
| Capteur d’image | Capteur CMOS ; 23,9 x 36 mm |
| Nombre total de pixels | 12,87 millions |
- Largeur de la main de l’adulte entre l’index et l’annulaire : 8,5 cm
3.1. À quel standard de capteur appartient le capteur de l’appareil utilisé ?
Selon l’extrait des caractéristiques de l’appareil réflex numérique utilisé : Capteur CMOS ; 23,9×36 mm
Cela correspond au format standard (voir tableau des standards de capteurs) Plein format (24×36 mm)
3.2. Déterminer à quelle distance des mains l’objectif doit être placé pour que l’image obtenue respecte la règle des tiers, c’est-à-dire pour que l’image de la main de l’adulte soit située entre les deux lignes des horizontales dites « des tiers ».
Le candidat est évalué sur ses capacités à concevoir et à mettre en œuvre une démarche de résolution, ainsi que sur la qualité de sa rédaction.
Toutes les prises d’initiative et toutes les tentatives de résolution, même partielles, seront valorisées.
Distance des mains l’objectif doit être placé : on cherche OA
Largeur de la main de l’adulte entre l’index et l’annulaire : 8,5 cm. Le capteur mesure 23,9 × 36 mm. Pour que l’image de la main de l’adulte soit située entre les deux lignes des horizontales dites « des tiers » on prend 1/3 de la hauteur du capteur :
$$A’B’=\frac{1}{3}\times23,9=7,97\ mm$$
On en déduit
$$\gamma=\frac{\overline{A’B’}}{\overline{AB}}=\frac{-7,97.10^{-3}}{8,5.10^{-2}}=-0,094$$
Or
$$\gamma=\frac{\overline{OA’}}{\overline{OA}}$$
Donc
$$\overline{OA’}=\gamma\ \overline{OA}$$
$$\overline{OA’}=-0,094\times\overline{OA}$$
Formule de conjugaison :
$$\frac{1}{\overline{OA’}}=\frac{1}{\overline{OA}}+\frac{1}{\overline{OF’}}$$
$$\frac{1}{\overline{OA’}}-\frac{1}{\overline{OA}}=\frac{1}{\overline{OF’}}$$
$$\frac{1}{-0,094\ \overline{OA}}-\frac{1}{\overline{OA}}=\frac{1}{\overline{OF’}}$$
$$\frac{1}{\overline{OA}}\left(\frac{1}{-0,094}-1\right)=\frac{1}{\overline{OF’}}$$
$$\frac{1}{\overline{OA}}\times-11,6=\frac{1}{\overline{OF’}}$$
$$\overline{OA}\times\frac{1}{-11,6}=\overline{OF’}$$
$$\overline{OA}=-11,6\times\overline{OF’}$$
$$\overline{OA}=-11,6\times50.10^{-3}=-0,58\ m$$
$$OA=0,58\ m=58\ cm$$
Pour que l’image obtenue respecte la règle des tiers, l’objectif doit être placé à 58 cm des mains.
Annexe à rendre avec la copie
Question 1.1.1.

