La plongée sous-marine en fosse

E3C2 – 10 points – Durée 1h – calculatrice autorisée

Sujet n°G1SPHCH02688 , n°G1SPHCH02696 , n°G1SPHCH02766 et n°G1SPHCH02769

Télécharger l’exercice en PDF :

Pour finaliser sa formation de niveau 1, un plongeur descend progressivement au fond de la fosse de plongée située à La Teste-De-Buch. La profondeur est le principal critère qui distingue une fosse de plongée d’une simple piscine. Cette fosse est composée d’une colonne d’eau de 20 mètres hors-sol et de 6 m de diamètre. Cette fosse permet aux plongeurs de s’entraîner dans une eau à 28 °C tout au long de l’année, et ce quelle que soit la météo.  

La plongée sous-marine

 […] Toute personne qui a déjà plongé le sait : la pression ambiante augmente à mesure que l’on s’enfonce sous l’eau […]. À 20 mètres de profondeur, elle est ainsi le triple de la pression atmosphérique (c’est-à-dire la pression qui règne à la surface de l’eau plus la pression due à la couche d’eau). Les tissus mous de notre organisme sont peu compressibles et ne changent quasiment pas de volume au cours d’une plongée.

En revanche, le comportement de l’air contenu dans le système respiratoire est tout autre. Les gaz sont beaucoup plus compressibles que les liquides. Dès le milieu du xvii^e siècle, l’Irlandais R. Boyle et le Français E. Mariotte énoncèrent une loi pour décrire leur compressibilité […]

Roland Lehoucq et Jean-Michel Courty  01 septembre 2001  POUR LA SCIENCE N° 287

Données :

• pression atmosphérique : 1,013 bar ; 1,0 bar = 1,0 x 10⁵ Pa ;
• masse volumique de l’eau : ρ = 1,0 x 10³ kg.m^-3 ;  
• intensité du champ de pesanteur : g = 9,81 N.kg^-1.

1. Pression à une profondeur donnée

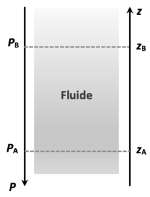
On s’intéresse dans cette partie à la loi fondamentale de la statique des fluides pour modéliser l’évolution de la pression atmosphérique en fonction de l’altitude. Cette loi précise que pour un fluide au repos incompressible de masse volumique ρ, la différence de pression entre deux points, A et B, s’exprime par la relation : P_A-P_B=ρ×g×(Z_A-Z_B)

Dans cette relation :

• la masse volumique ρ s’exprime en kg×m^-3 ;
• l’intensité de pesanteur g s’exprime en  N×kg^–1 ;
• les altitudes z_A et z_B s’expriment en m et sont repérées sur un axe vertical  ascendant  Oz.

1.1. Décrire qualitativement comment la pression dans l’eau évolue lors de la descente du plongeur dans la fosse.

D’après la loi fondamentale de la statique des fluides :
$P_B-P_A=\rho\times g\times(z_A-z_B)$
$-P_A=\rho\times g\times(z_A-z_B)-P_B$
$P_A=-\rho\times g\times(z_A-z_B)+P_B$

Or $z_A<z_B$
d’ou $(z_A-z_B)<0$
$\rho\times g\times(z_A-z_B)<0$
$-\rho\times g\times(z_A-z_B)>0$

d’ou $P_A>P_B$

La pression augmente lorsque le plongeur descend dans la fosse de plongée

1.2. Justifier, à l’aide de la relation de la statique des fluides, la phrase : « À 20 mètres de profondeur, elle est ainsi le triple de la pression atmosphérique (c’est-à-dire la pression qui règne à la surface de l’eau plus la pression due à la couche d’eau). »

$P_B-P_A=\rho\times g\times(z_A-z_B)$
$P_A=-\rho\times g\times(z_A-z_B)+P_B$
$P_A=-1,0.10^3\times9,81\times(0-20)+1,0.10^5$
$P_A=3,0.10^5\ Pa$

Or $P_B=1,0.10^5\ Pa$ donc $P_A=3P_B$

Il est possible de vérifier la loi fondamentale de la statique des fluides au laboratoire.

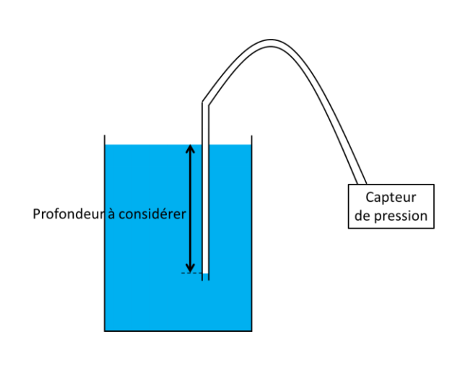
Pour cela, on réalise une série de mesures de la pression P au sein d’un liquide en fonction de la profondeur h à l’aide du dispositif ci-contre.

Le protocole expérimental est le suivant :

• déplacer verticalement, dans une éprouvette contenant un liquide, un tube de verre relié à un tuyau souple branché à un capteur de pression lui-même relié à une interface d’acquisition. Ce capteur mesure la pression en kPa ;
• faire une première mesure de pression à la surface ;
• relever ensuite les valeurs de pression pour des profondeurs croissantes en descendant progressivement le tube en verre dans l’éprouvette ;
• les valeurs mesurées permettent de représenter le graphe P en fonction de h à l’aide d’un tableur. On obtient alors une droite modélisée par le tableur par l’équation mathématique suivante :

P = 9,771 x 10³ x h + 101,3 x 10³ ; P est exprimée en Pa et h en m.

1.3. Que représente la valeur de la pression P₀ à la profondeur h = 0 m ?

$P=9,771\times10^3\times h+101,3\times10^3$
$P_0=P_{(h=0)}=9,771\times10^3\times0+101,3\times10^3$
$P_0=101,3\times10^3=1,013.10^5Pa$
$P_0$ représente la pression atmosphérique

1.4. Expliquer pourquoi les mesures expérimentales sont compatibles avec la loi fondamentale de la statique des fluides.

$P=9,771\times10^3\times h+101,3\times10^3$
$P=9,771\times10^3\times h+P_0$
$P-P_0=9,771\times10^3\times h$

Loi fondamentale de la statique des fluides :
$P_B-P_A=\rho\times g\times(z_A-z_B)$
$P_B-P_A=\rho\times g\times h$

L’équation mathématique obtenue est compatible avec la loi fondamentale de la statique des fluides

1.5. Citer des sources d’erreurs possibles dans ce protocole expérimental.

2. Autonomie d’un plongeur

Lors de la plongée en bouteille le détendeur permet au plongeur de respirer de l’air à la même pression que la pression à la profondeur où il se trouve. Mais toute plongée en bouteille s’effectue avec une quantité limitée d’air. Il est donc indispensable de savoir contrôler la consommation de cette quantité d’air au cours de la plongée afin de pouvoir effectuer une remontée et d’éventuels paliers. Cela passe par l’évaluation de son autonomie en air en fonction de la profondeur. Il existe différentes méthodes de calcul de l’autonomie, la plus simple consiste à calculer le volume d’air disponible à la profondeur donnée et de tenir compte de l’air consommé par minutes.

D’après www.cdp-plongee.com 

2.1. On note V₁ le volume d’air disponible dans la bouteille de plongée lorsqu’elle est mise sous pression à la pression P₁ et V₂ celui d’air disponible pour le plongeur lorsque qu’il est à la pression P₂. Les températures sont supposées identiques dans les deux situations.

En utilisant la loi de Mariotte, écrire la relation liant V₁, P₁,V₂ et P₂.

Loi de Mariotte : $P\times V=Constante$
$P_1\times V_1=P_2\times V_2$

2.2. En supposant que la consommation en volume d’air du plongeur reste toujours la même au cours de la plongée, expliquer sans calcul comment l’autonomie en air du plongeur évolue avec la profondeur.

Lorsque la profondeur augmente, la pression augmente (voir question 1.1)

$V_2=\frac{P_1\times V_1}{P_2}$

$V_2$ est inversement proportionnel à $P_2$. Ainsi lorsque la pression augmente le volume $V_2$ diminue.

On en déduit que l’autonomie du plongeur diminue avec la profondeur.

2.3. Le plongeur dispose d’une bouteille de plongée d’une capacité de 12 litres mise sous pression à la pression initiale de 200 bars. 

Soit :
$P_1$ la pression dans la bouteille : $P_1=200\ bar$
$V_1$ le volume de la bouteille : $V_1=12\ L$
$P_2$ la pression à 20m de profondeur : $P_2=3,0.10^5\ Pa$ (voir question 1.2)

$P_1\times V_1=P_2\times V_2$
$V_2=\frac{P_1\times V_1}{P_2}$
$V_2=\frac{200\times1,0.10^5\times12}{3,0.10^5}=800\ L$

Or il consomme $15L$ par minutes. Il dispose de :
$t=\frac{800}{15}=53\ min$

En utilisant la loi de Mariotte, calculer la durée durant laquelle le plongeur peut rester dans la fosse à 20 m de profondeur sachant qu’il consomme 15 litres d’air par minute.

En réalité le plongeur doit toujours calculer son autonomie en tenant compte d’une marge de sécurité. Pour remonter en surface en ayant conservé une pression de 50 bars dans sa bouteille : c’est ce qu’on appelle communément « la réserve ».

2.4. La prise en compte de cette réserve réduit-elle ou augmente-t-elle la durée de la plongée ? Justifier sans calcul.

Le temps de plongée est proportionnel au volume disponible. La prise en compte de la « réserve » diminue le volume disponible.
Ainsi, la prise en compte de cette réserve diminue la durée de la plongée.

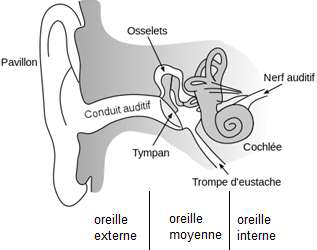
3. La manœuvre de Valsalva

En plongée, la différence de pression de part et d’autre du tympan peut provoquer une vive douleur. La manœuvre de Vasalva consiste à souffler par le nez, bouche fermée et nez pincé afin de faire pénétrer de l’air dans l’oreille moyenne. L’air extérieur passe par la trompe d’Eustache.   https://fr.wikibooks.org

3.1. Rappeler la relation entre la pression P, la norme F de la force pressante et l’aire S de la surface sur laquelle elle s’exerce.

$F=P\times S$

3.2. Évaluer la valeur de la norme de la force pressante F₁ exercée par l’air emprisonné dans l’oreille moyenne à la pression de 1,0 bar sur la paroi interne du tympan dont la surface est de 70 mm².

$F=P\times S$
$F=1,0.10^5\times70\times(10^{-3})^2$
$F=7,0\ N$

3.3. La valeur de la norme de la force pressante F₂ exercée par l’eau sur la paroi externe du tympan pour un plongeur situé à 20 m de profondeur est de 21 N.

Pas de question dans le sujet !!!

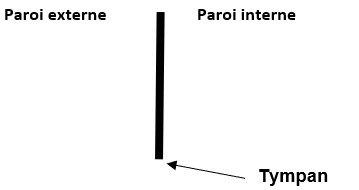
3.4. Reproduire sur la copie et compléter le schéma ci-dessous, en représentant les forces pressantes exercées sur le tympan :

• $\overrightarrow{F_1}$ la force pressante exercée par l’air emprisonné dans l’oreille moyenne ;
• $\overrightarrow{F_2}$ la force pressante exercée par l’eau sur la paroi externe du tympan.

Échelle :   1 cm pour 7 N.

En déduire pourquoi le plongeur ressent une vive douleur lors de la descente.

Échelle : $1\ cm$ pour $7\ N$.
Pour $\overrightarrow{F_1}$ , on représente la force par un vecteur de $1\ cm$
Pour $\overrightarrow{F_2}$ , on représente la force par un vecteur de $3\ cm$

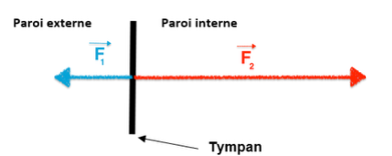
Les forces exercées sur la paroi du tympan ne s’annulent pas.
C’est pourquoi le plongeur ressent une vive douleur lors de la descente.

3.5. Expliquer pourquoi la manœuvre de Vasalva permet de compenser la pression de l’eau introduite dans le conduit auditif.

« La manœuvre de Vasalva consiste à souffler par le nez, bouche fermée et nez pincé afin de faire pénétrer de l’air dans l’oreille moyenne. »

Cette manœuvre permet d’augmenter le nombre de molécule d’air pour un même volume et donc augmente la pression intérieure :  augmente.

La différence de force exercée sur la paroi diminue.

Ainsi, la manœuvre de Vasalva permet de compenser la pression de l’eau introduite dans le conduit auditif.

Télécharger l’exercice en PDF :