E3C2 – 10 points – Durée 1h – calculatrice autorisée
Sujet n°G1SPHCH02773, n°G1SPHCH02730 et n°G1SPHCH02720
Télécharger l’exercice en PDF :
Le dernier record du monde de vitesse sur rail du TGV (Train à Grande Vitesse) a été homologué le 3 avril 2007. Une rame expérimentale a atteint à 13h14 la vitesse de 574,8 km·h−1 sur la toute nouvelle ligne Est européenne.
Le mur de la caténaire
L’alimentation des moteurs électriques du TGV est réalisée à l’aide de la caténaire et du pantographe.
La caténaire (voir figure ci-contre) est le câble électrique tendu au-dessus des voies. Le pantographe (voir figure ci-contre)est le dispositif articulé fixé sur le toit de la locomotive, permettant une liaison électrique par frottement sur la caténaire.

Le pantographe appuie sur le câble et le soulève, créant une déformation en forme de V inversé. Lorsque le train se déplace, une onde mécanique progressive se propage dans la caténaire devant la locomotive. Si le train rattrape l’onde, le contact entre le pantographe et la caténaire est rompu et la puissance électrique transmise aux moteurs diminue. La célérité de l’onde dans la caténaire est une contrainte qui limite la vitesse du train, on parle d’un « mur de la caténaire » par analogie avec le mur du son.
1. L’onde qui se propage dans la caténaire est progressive et mécanique. Rappeler la définition d’une onde progressive puis indiquer ce qui permet de la qualifier de mécanique.
Une onde progressive mécanique est la propagation d’une perturbation dans un milieu matériel sans transport de matière et avec transport d’énergie.
Cette onde est qualifiée de mécanique car elle se déplace dans un milieu matériel (le câble) et ne se propage pas dans le vide.
Un système de poulies et de contrepoids permet de tendre plus ou moins la caténaire. Pour étudier l’influence de cette tension mécanique T (en Newton), on utilise un logiciel de simulation mis en ligne par l’université du Colorado. Dans cette simulation la caténaire du train est modélisée par la corde sur laquelle se propage une perturbation. Deux captures d’écran de ce logiciel sont données ci-dessous.
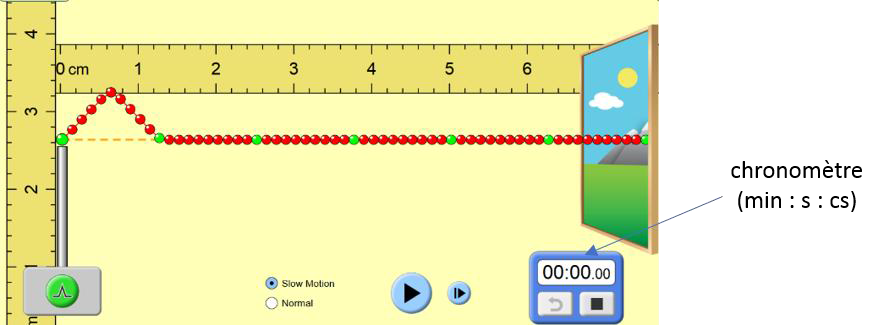
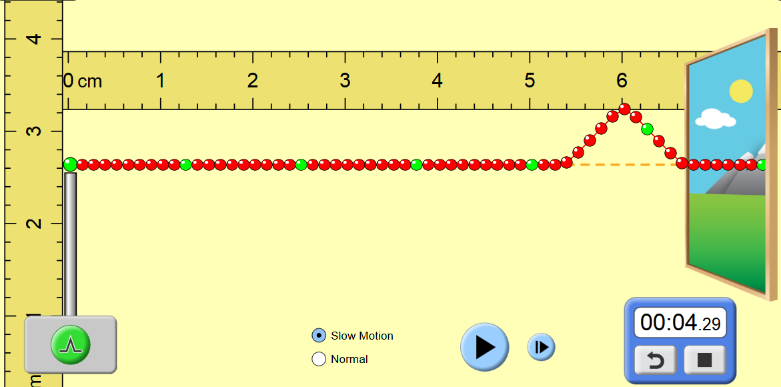
2. Déterminer, à l’aide des deux captures ci-dessus la valeur de la vitesse de propagation de l’onde dans la simulation.
$v=\frac{d}{t}$
$v=\frac{5,4.10^{-2}}{4,29}=1,3.10^{-2}\ m.s^{-1}$
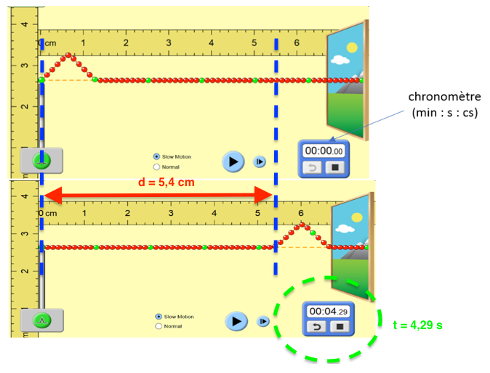
3. Une deuxième simulation avec une valeur de tension plus élevée du câble donne une célérité de 6,3×10-2 m·s-1. Indiquer l’influence du paramètre tension sur la célérité de l’onde.
Avec une tension plus élevée, on obtient une célérité plus grande. On en déduit donc que lorsque la tension augmente la célérité augmente.
L’expression littérale de la célérité de l’onde mécanique qui se propage dans la caténaire est :
$c=\sqrt{\frac{T}{\rho \times S}}$ (1)
avec :
- c la célérité de l’onde en mètres par seconde (m·s-1) ;
- T la tension exercée sur la caténaire en Newton (N) ;
- S la section de la caténaire (m2) ;
- ρ la masse volumique du matériau constitutif du câble (kg·m−3).
La SNCF a spécifié que pour des trajets commerciaux, la vitesse de ses TGV ne devait pas dépasser 70 % de la vitesse de propagation des ondes dans la caténaire.
Nous disposons des informations suivantes sur les caténaires utilisées :
| Tension T (N) | Section S (mm2) | Masse volumique ρ du cuivre (kg·m−3) |
| 2,6×104 | 150 | 8920 |
4. Vérifier la cohérence de cette relation avec les résultats obtenus lors de la simulation.
$c=\sqrt{\frac{T}{\rho.S}}$
c est proportionnel à racine de T : lorsque la tension augmente la célérité augmente.
Ainsi la formule est cohérente avec les résultats obtenus lors de la simulation.
5. Déterminer, en m·s−1 puis en km·h−1, la valeur de la vitesse théorique maximale que ne doit pas dépasser un TGV en exploitation commerciale.
$c=\sqrt{\frac{T}{\rho.S}}$
$c=\sqrt{\frac{2,6.10^4}{8920\times150.10^{-6}}}=139\ m.s^{-1}=500\ Km.h^{-1}$
La SNCF a spécifié que pour des trajets commerciaux, la vitesse de ses TGV ne devait pas dépasser 70 % de la vitesse de propagation des ondes dans la caténaire.
Soit
$v=\frac{70}{100}\times c=\frac{70}{100}\times139=97\ m.s^{-1}=349\ Km.h^{-1}$ (On multiplie par 3,6 pour passer en Km.h-1)
La valeur de la vitesse théorique maximale que ne doit pas dépasser un TGV en exploitation commerciale est de 349 Km.h−1.
6. Proposer une argumentation d’une dizaine de lignes en indiquant sur quels paramètres les ingénieurs ont pu agir pour repousser le mur de la caténaire et ainsi faire franchir au TGV la barre symbolique des 500 km·h−1.
On précisera dans le raisonnement les paramètres modifiés, le sens d’évolution de leurs valeurs (plus élevée ou plus faible) ainsi que le choix le plus approprié et le plus économique.
Pour augmenter la vitesse du TGV, il faut augmenter c.
Or
$c=\sqrt{\frac{T}{\rho.S}}$
On peut :
Augmenter T car proportionnel à c
Diminuer $\rho$ en choisissant un matériau conducteur ayant une masse volumique plus faible car inversement proportionnel à c
Diminuer S car inversement proportionnel à c
Les ingénieurs doivent penser également au cout des matériaux et aux propriétés mécaniques.
Changer de matériau est difficilement envisageable car le cuivre est un bon conducteur et il est le meilleur rapport qualité prix.
Diminuer S risque de rentre le câble trop fragile.
Le choix le plus approprié est donc d’augmenter la tension du câble.
Freinage d’urgence et distance de freinage
Un TGV commercial de masse M = 425 t roulant à la vitesse v0 = 320 km·h−1 sur une voie que l’on supposera rectiligne et horizontale doit effectuer un arrêt d’urgence. La valeur de la distance nécessaire pour que le TGV s’immobilise (distance d’arrêt) est de 3,2 km.
Au cours d’un essai dans la phase de préparation du record, un incident a déclenché le freinage d’urgence et la rame expérimentale (de masse M’ = 270 t roulant à la vitesse v1 = 501,6 km·h−1) s’est immobilisée au bout de 15 km.
7. À l’aide d’une approche énergétique, justifier le sens de l’évolution de cette distance d’arrêt.
$E_c=\frac{1}{2}m.v^2$
$E_{c(0)}=\frac{1}{2}M\times v_0^2=\frac{1}{2}\times425.10^3\times(\frac{320}{3,6})^2=1,67.10^9J$
$E_{c(1)}=\frac{1}{2}M’\times v_1^2=\frac{1}{2}\times270.10^3\times(\frac{501,6}{3,6})^2=2,62.10^9J$
$E_{c(1)}>E_{c(0)}$
La distance d’arrêt dépend de l’énergie cinétique , c’est pourquoi $d_1>d_0$
Alimentation électrique des moteurs
Pour fournir plus de puissance aux moteurs électriques de la rame, la tension électrique de la caténaire a été portée à 31 kV contre 25 kV en temps normal. Lors des essais, la valeur de l’intensité du courant traversant le pantographe est en moyenne égale à 800 A.
8. Calculer la valeur de la puissance électrique fournie par la caténaire aux moteurs électriques.
$P=U\times I$
$P=31.10^3\times800=2,5.10^7W$
La puissance restituée par l’ensemble des moteurs a été estimée à 19 600 kW (soit plus du double de celle d’une rame de TGV classique).
9. Recopier et compléter le schéma suivant qui représente le bilan de puissance des moteurs de la rame.


10. Exprimer et calculer le rendement de l’ensemble des moteurs de la rame expérimentale. Expliquer pourquoi il ne peut être supérieur à 1.
$\eta=\frac{P_{mécanique}}{P_{electrique}}=\frac{19600.10^3}{2,5.10^7}=0,78=78%$
Le rendement est le rapport de la puissance reçue par la puissance utile. Ainsi au maximum le rendement vaut 1 (s’il n’y a aucune perte énergétique).
