E3C2 – 10 points – Durée 1h – calculatrice autorisée
Sujet n°G1SPHCH02751
Télécharger l’exercice en PDF :
Partie 1 : fabriquer des vagues artificielles lors des JO de 2024
Les jeux olympiques représentent un évènement sportif majeur, qui a lieu tous les quatre ans. Paris accueillera les jeux olympiques en 2024, tandis que ceux de 2020 auront lieu à Tokyo.
De nouveaux sports, tels que le surf, ont été ajoutés aux quarante disciplines existantes, ce qui contraint les pays d’accueil à disposer de nouveaux équipements.
Ainsi, un projet de piscine à vague sur la Ville de Sevran, en Île-de-France, est à l’étude et devrait voir le jour en 2023. Il s’agit ici, de construire un parc de loisir, notamment aquatique ; dans lequel viendrait s’intégrer les plans d’eaux olympiques. Concernant la piscine dédiée à la pratique du surf, une technologie inédite permettra d’obtenir 1 000 vagues par heure alors que les technologies des piscines actuelles sont en dessous de cette performance.

1. Définir d’une onde mécanique.
On appel onde mécanique, le phénomène de propagation d’une perturbation dans un milieu matériel sans transport de matière, mais avec transport d’énergie.
2. À partir des informations contenues dans l’énoncé, déterminer la valeur de la fréquence des vagues formées, puis en déduire la périodicité temporelle.
La fréquence d’un phénomène périodique correspond au nombre de fois où le phénomène se répète par seconde.
$f=\frac{1000}{3600}=0,28\ Hz$
Or
$f=\frac{1}{T}$ , $T=\frac{1}{f}$
$T=\frac{1}{0,28}=3,6\ s$
3. En exploitant le document ci-dessus, déterminer la période spatiale des vagues formées.
Echelle : 1cm ⟺ 10,5 m
sur le schéma on mesure 7,6cm soit $7,6\times10,5=79,8\ m$
$5\lambda=79,8\ $
$\lambda=\frac{79,8\ }{5}=16,0\ m$

4. En déduire la vitesse de propagation de cette onde.
$v=\frac{\lambda}{T}$
$v=\frac{16,0}{3,6}=4,4\ m.s^{-1}$
Partie 2 : les tsunamis aux vagues destructrices
Les tsunamis se forment généralement à la suite de divers phénomènes tels que les éruptions volcaniques sous-marines, les glissements de terrains, les chutes d’astéroïdes dans les océans. Le cas le plus fréquent reste celui des séismes dont l’épicentre se trouve sous l’océan.
En 2011 un séisme de magnitude 9,0 a eu lieu au large du Japon. L’épicentre était localisé sous l’océan Pacifique, à 370 km du Nord-Est du Japon. Les études montrent que l’onde sismique, générée par le mouvement de subduction des deux plaques tectoniques avoisinantes, a atteint la côte japonaise 150 secondes après sa formation. Le séisme a été ressentie à 14 h 46 min 00 s heure locale soit à 5 h 46 min 00 s dans l’échelle de temps universel.
Ce séisme sous-marin a été à l’origine d’un énorme tsunami qui traversa tout l’océan pacifique. De nombreux pays ont été touchés par la houle. C’est le cas d’une des îles de l’archipel des marquises. En effet, l’île de Nihu ku Hiva a été touchée à 17 h 49 min 00 s dans l’échelle de temps universel. Cette île se trouve à 9 900 km de l’épicentre du séisme.
Temps universel : il s’agit de l’heure de référence internationale.
1. Déterminer l’heure à laquelle s’est formé le tsunami au large du Japon.
« l’onde sismique … a atteint la côte japonaise 150 secondes après sa formation. Le séisme a été ressentie à 14 h 46 min 00 s heure locale »
14 h 46 min 00 s-150s = 14 h 46 min 00 s – 2 min 30 s =14 h 43 min 30 s
2. En déduire la valeur de la vitesse moyenne de propagation v1 de l’onde sismique, l’exprimer en m.s-1.
L’épicentre était localisé sous l’océan Pacifique, à 370 km du Nord-Est du Japon.
$v=\frac{d}{\Delta t}$
$v=\frac{370.10^3}{150}=2,47.10^3\ m.s^{-1}$
3. Déterminer la valeur de la vitesse moyenne v2 de propagation du tsunami en m.s-1.
« Ce séisme sous-marin a été à l’origine d’un énorme tsunami … Nihu ku Hiva a été touchée à 17 h 49 min 00 s dans l’échelle de temps universel. Cette île se trouve à 9 900 km de l’épicentre du séisme. »
Le tsunami a été créé par l’onde sismique à 14 h 43 min 30 s heure locale (voir question 1), soit 5 h 43 min 30 s
$\Delta t=17\ h\ 49\ min\ 00\ s-5\ h\ 43\ min\ 30\ s$
$\Delta t=12\ h\ 5\ min\ 30\ s$
$v=\frac{d}{\Delta t}$
$v=\frac{9900.10^3}{12\times3600+\ 5\times60+\ 30}=227\ m.s^{-1}$
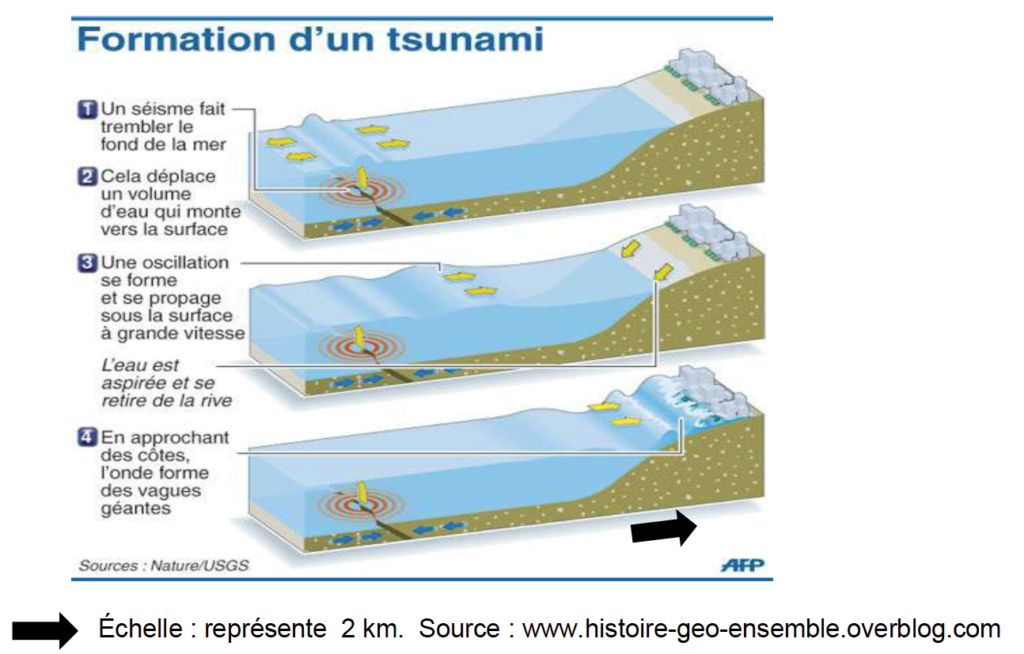
On considère que le document précédant représente le cas du tsunami de Nihu ku Hiva. En supposant la valeur de la vitesse moyenne v2 de propagation des vagues à la surface de l’eau constante, déterminer la durée dont dispose un habitant au bord de mer pour se mettre à l’abri dès lors que la mer se retire.
Echelle : 1cm ⟺ 2 km
sur le schéma on mesure 2,2 cm soit $2,2\times2=4,4\ km$
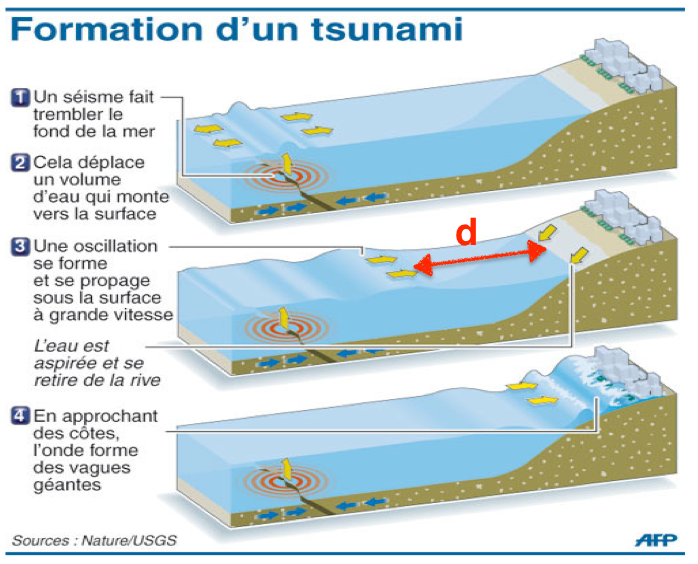
$v=\frac{d}{\Delta t}$
$\Delta t=\frac{d}{v}$
$\Delta t=\frac{4,4.10^3}{227}=19\ s$
Un habitant au bord de mer dispose de 19s pour se mettre à l’abri dès lors que la mer se retire.
