Performances d’un cycliste

E3C2 – 10 points – Durée 1h – calculatrice autorisée

Sujet n°G1SPHCH02724 n°G1SPHCH02740 , n°G1SPHCH02745 et n°G1SPHCH02780

Télécharger l’exercice en PDF :

Les performances des champions du cyclisme sur route, mises en avant tous les ans à l’occasion du Tour de France par exemple, ont de quoi impressionner. Leurs performances permettent de parcourir des centaines de kilomètres à vélo en atteignant des vitesses moyennes de l’ordre de 40 km/h.

Les performances d’un cycliste professionnel

[… ] La vitesse moyenne du dernier vainqueur, Christopher Froome, sur la longueur des 21 étapes du Tour de France 2016, s’élève à 39,571 km/h. C’est beaucoup moins que Lance Armstrong (41,654 km/h) en 2005, mais à peine moins que Marco Pantani (39,983 km/h) en 1998. […] Dans cet ordre d’idée, le même Froome, en 2015, a grimpé la longue (20 km) et difficile (4,3°) d’inclinaison moyenne par rapport à l’horizontale) montée du Mont Ventoux en un temps exceptionnel de 57 minutes et 30 secondes, pour une vitesse moyenne de 20,869 km/h.
                                                                      D’après www.lci.fr/cyclisme/video-tour-de-france-2017

Puissance de pédalage d’un cycliste

Un moyen de comparer les coureurs est le rapport puissance/masse. […]. Lorsqu’on cherche à progresser, on optimise le rapport puissance/masse. Voici quelques exemples de ce rapport puissance/masse (en W/kg) en fonction du niveau :

sur une heure :

• environ 5,7 W/kg : professionnel de très haut niveau ;
• environ 4,7 W/kg : amateur de très bon niveau ;
• environ 3,5 W/kg : amateur moyen ;
• environ 2,5 W/kg : cycliste occasionnel.
                         D’après www.velochannel.com/cest-quoi-la-puissance-en-cyclisme-32808

Données :

• intensité de la pesanteur g = 9,8 m.s^-2 ;
• masse de Christopher Froome : m₁ = 68 kg (d’après Wikipédia) ;
• masse de son vélo : m₂ = 7,0 kg ;
• dénivelé vertical parcouru lors de la montée du Mont Ventoux : H = 1,5 km.

1. Étude mécanique du système S : {Vélo + cycliste}

On commence par s’intéresser à une portion de route rectiligne d’inclinaison constante : dans la réalité, on peut estimer que la route est une succession de portions de route de ce type.
De plus, pour passer de la réalité de la course à un modèle physique simple, on choisit les hypothèses simplificatrices suivantes :

• on néglige les frottements avec l’air et le contact sol-roue avant ;
• on considère que la valeur de la vitesse de Froome reste constante sur cette portion rectiligne d’inclinaison constante ;
• on néglige la contribution de la rotation des roues à l’énergie cinétique totale.

1.1. Définir le référentiel adapté à l’étude du mouvement du système S.

Le référentiel le plus adapté est le référentiel terrestre, supposé galiléen.

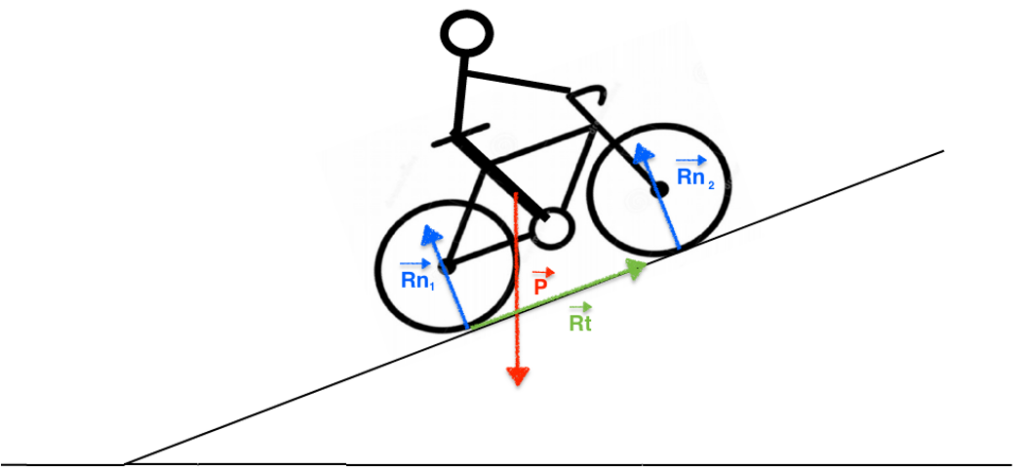
1.2. Représenter les forces extérieures agissant sur ce système.

1.3. Compte tenu de la nature du mouvement de l’ensemble {Vélo + cycliste}, que peut-on en déduire sur la résultante des forces ? Écrire la relation correspondante entre vecteurs.

« On considère que la valeur de la vitesse de Froome reste constante sur cette portion rectiligne d’inclinaison constante »

Le mouvement est rectiligne uniforme. D’après la 1ere loi de Newton (principe d’inertie) : $\sum \overrightarrow{F}=\overrightarrow{0}$

1.4. En projetant sur un axe défini par la piste, en déduire que c’est la réaction tangentielle du sol sur la roue arrière qui « empêche le système de ralentir ».

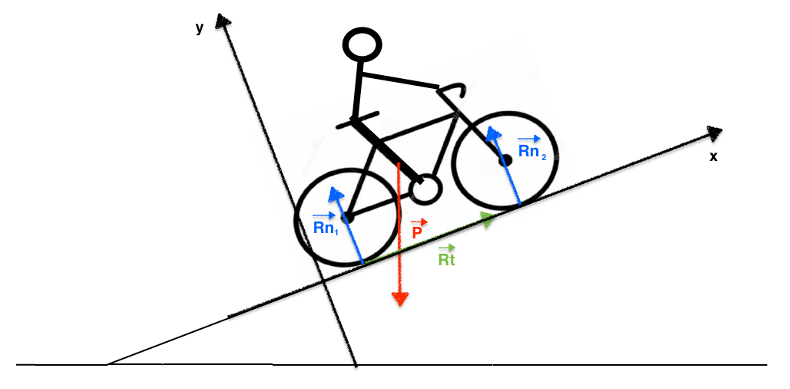
C’est donc la réaction tangentielle du sol sur la roue arrière qui « empêche le système de ralentir ».

2. Étude énergétique du système {Vélo + cycliste} et simulation numérique

L’objectif est d’estimer avec nos hypothèses simplificatrices la valeur de la vitesse du cycliste.

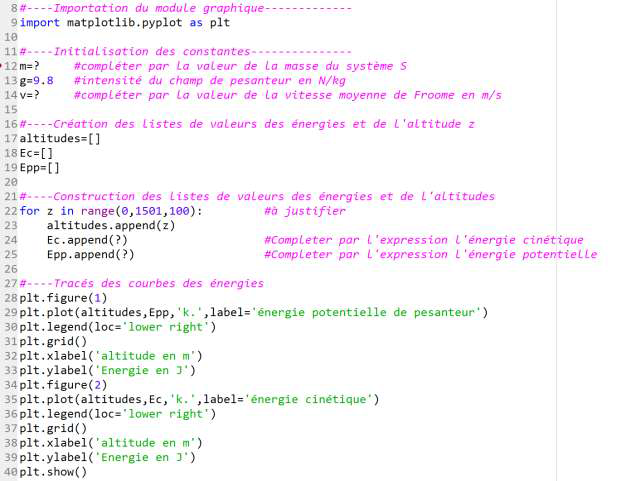
Une simulation écrite en langage Python pour analyser l’évolution des énergies est présentée dans l’annexe à rendre avec la copie.

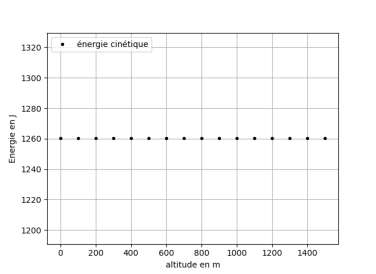
Voici les résultats obtenus :

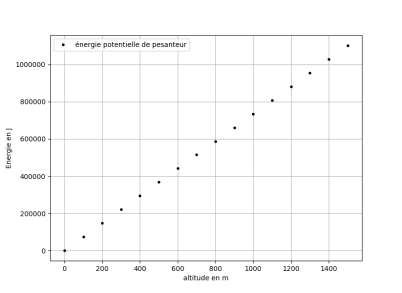
Le code du programme est incomplet.

2.1. Répondre aux questions écrites sur l’annexe à rendre avec la copie en respectant les contraintes suivantes :

• l’origine des altitudes correspond au point A : point de départ de la course ;
• la piste est rectiligne et d’inclinaison constante jusqu’au point d’arrivée B de la course ;
• l’origine de l’énergie potentielle de pesanteur est aussi le point A ;
• on veut construire un graphique composé d’un point tous les 100 mètres.

Rappel : +, – ,* , /, ** désignent respectivement l’addition, la soustraction, la multiplication, la division et l’exponentiation des nombres (flottants ici).

Numéro de la ligne du code python	le symbole « ? » est remplacé par :	Justification (non demandée)
12	75	m= m1+ m2=68+7=75Kg
14	5.797	$v=\sqrt{\frac{2E_c}{m}}=\sqrt{\frac{2\times1260}{75}}=5,797\ m.s^{-1}$
24	0.5*m*v**2	$E_C=\frac{1}{2}\times m\times v^2$
25	m*g*z	$E_{pp}=m\times g\times z$

Ligne 22 :                  Pourquoi écrit-on : range (0,1501,100) ?
Réponse : « –           on veut construire un graphique composé d’un point tous les 100 mètres. »

range (0,1501,100) : 0 pour la valeur de l’altitude de départ, 1501pour la valeur de l’altitude finale, 100 pour le pas de 100m.

Ainsi, les valeurs des altitudes seront : 0 ;100 ;200 ;300 ;400 ;… ;1500

2.2. Le programme en Python permet d’obtenir les deux graphiques ci-dessus. Justifier l’évolution observée de l’énergie cinétique.

La vitesse du cycliste est constante donc son énergie cinétique est constante.
$E_C=\frac{1}{2}\times m\times v^2$

2.3. Donner l’expression de la variation d’énergie potentielle de pesanteur sur cette portion de piste en fonction notamment de la longueur AB de la piste et de son inclinaison caractérisée par l’angle α que la piste fait avec la ligne horizontale.

$\Delta E_{pp}=m\times g\times(z_B-z_A)$

Or
$\sin(\alpha)=\frac{(z_B-z_A)}{AB}$
$(z_B-z_A)=AB\times\sin(\alpha)$

d’ou
$\Delta E_{pp}=m\times g\times AB\times\sin(\alpha)$

On admet qu’en l’absence de glissement des roues du vélo sur la route, la réaction $\overrightarrow{R}$ du sol sur les roues ne travaille pas : $ W_{AB}(\overrightarrow{R})=0$ . On prend en compte la puissance musculaire fournie au système par Christopher Froome par l’intermédiaire du pédalage : P_musculaire.

2.4. Faire un bilan d’énergie mécanique pour le système et en déduire la relation suivante :
P_musculaire.Δt = (m₁ + m₂).g. AB.sin(α).

La variation d’énergie mécanique du système est due à l’énergie apporté par le cycliste en pédalant (on néglige ici les forces de frottements).
$\Delta E_m=E_{cycliste}$
$\Delta E_{pp}+\Delta E_C=P_{musculaire}\times\Delta t$
$m\times g\times AB\times\sin(\alpha)=P_{musculaire}\times\Delta t$
$P_{musculaire}\times\Delta t=m\times g\times AB\times\sin(\alpha)$

2.5. Estimer la vitesse moyenne de Christopher Froome dans le cadre de ce modèle, en utilisant la relation établie à la question 2.4. et en utilisant les documents fournis en introduction.

La vitesse moyenne est définie par :
$v=\frac{d}{\Delta t}$
$v=\frac{AB}{\Delta t}$

Or d’après la question 2.4 :
$P_{musculaire}\times\Delta t=m\times g\times AB\times\sin(\alpha)$
$\Delta t=\frac{m\times g\times AB\times\sin(\alpha)}{P_{musculaire}}$

d’ou
$v=\frac{AB}{\frac{m\times g\times AB\times\sin(\alpha)}{P_{musculaire}}}$
$v=AB\times\frac{P_{musculaire}}{m\times g\times AB\times\sin(\alpha)}$
$v=\frac{P_{musculaire}}{m\times g\times\sin(\alpha)}$
$v=\frac{5,7\times68}{75\times9,8\times\sin(4,3)}$
$v=7,0\ m.s^{-1}$

2.6. Comparer à la valeur de la vitesse moyenne de Froome donnée par l’énoncé en proposant une critique du modèle adopté.

Pour trouver la vitesse en km.h$^{-1}$, on multiplie par 3,6
$v=7,0\times3,6=25\ km.h^{-1}$

D’après le texte : « pour une vitesse moyenne de 20,869 km/h. »
Cet écart s’explique car nous n’avons pas pris en compte les forces de frottements.

Annexe à rendre avec la copie

Partie 2, question 2.1.

Numéro de la ligne du code python	le symbole « ? » est remplacé par :
12
14
24
25

Télécharger l’exercice en PDF :