E3C2 – 10 points – Durée 1h – calculatrice autorisée
Sujet n°G1SPHCH02746 et n°G1SPHCH02771
Télécharger l’exercice en PDF :
Les feuilles de certaines plantes comme celles des vignes, des rosiers, des pêchers peuvent parfois jaunir tout en gardant des nervures bien vertes. C’est le signe que ces plantes souffrent de chlorose ferrique. Le fer, comme le magnésium, le manganèse ou le zinc sont essentiels à la synthèse de la chlorophylle, et les plantes les puisent dans le sol. Lorsque ces éléments manquent, la chlorophylle n’est plus synthétisée et les feuilles perdent leur couleur verte.
Il est possible de lutter contre la chlorose ferrique grâce à des moyens biologiques ; l’utilisation d’un purin d’ortie peut y contribuer par exemple.
Il est aussi possible d’utiliser des produits phytosanitaires commerciaux. La teneur en fer d’un produit phytosanitaire anti-chlorose est indiquée sur son emballage : 6,0 % en masse.
L’objectif de cet exercice est d’envisager un titrage par spectrophotométrie adapté au contrôle de qualité de ce produit.
Données :
Masse molaire atomique du fer : MFe = 56,0 g.mol-1
Couples oxydant/réducteur :MnO4–/Mn2+ (incolore) ; S2O82-/SO42-(incolore) ;
Fe3+(orange pâle)/Fe2+(vert pâle)
Spectre d’absorption d’une solution de permanganate de potassium de
concentration 2,5×10-4 mol.L-1.
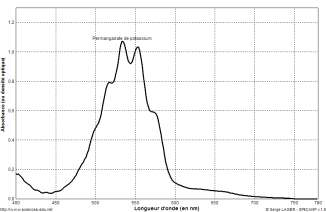
Spectre d’absorption d’une solution de peroxodisulfate de potassium de concentration 2,5×10-4 mol.L-1
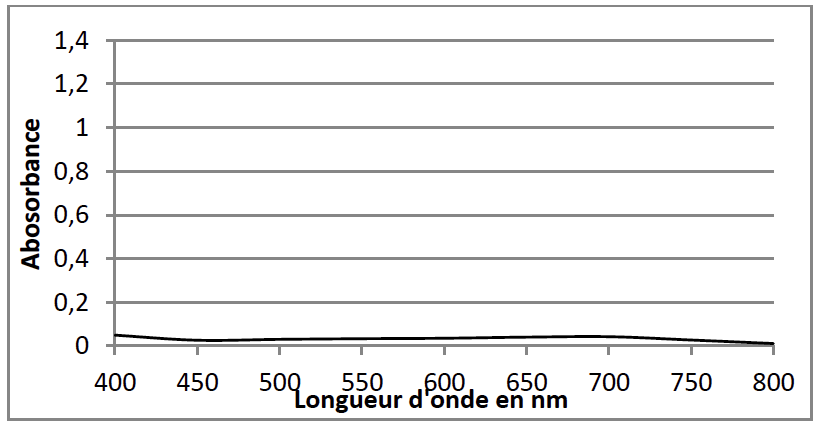
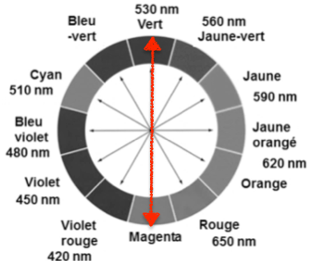
- Cercle chromatique
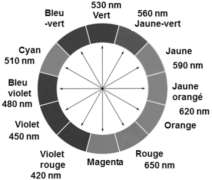
- Tests caractéristiques des ions Fe2+ et Fe3+ avec une solution aqueuse d’hydroxyde de sodium
| ions | couleur | Ajout de quelques gouttes de solution d’hydroxyde de sodium |
| Fe2+ | Vert à peine perceptible | Précipité vert d’hydroxyde de fer II |
| Fe3+ | Rouille à peine perceptible | Précipité rouille d’hydroxyde de fer III |
1. Choix du réactif titrant.
Pour réaliser le titrage des ions ferreux, Fe2+, contenus dans un produit phytosanitaire destiné à lutter contre la chlorose ferrique, on dispose de deux solutions titrantes possibles :
- Une solution de peroxodisulfate de potassium acidifiée (K+(aq)+S2O82-(aq)) de concentration 0,10 mol.L-1
- Une solution de permanganate de potassium acidifiée (K+(aq)+MnO4–(aq)) de concentration molaire 0,10 mol.L-1.
Les ions peroxodisulfate comme les ions permanganate réagissent en solution aqueuse avec les ions Fe2+. Un test avec une solution aqueuse d’hydroxyde de sodium, après réaction entre les ions Fe2+ et les ions S2O82- ou MnO4–, conduit au même précipité rouille d’hydroxyde de fer III.
1.1. Préciser la nature de la transformation chimique qui se produit quand on mélange des ions Fe2+ et des ions peroxodisulfate S2O82- d’une part ou permanganate MnO4– d’autre part, que le test avec une solution aqueuse d’hydroxyde de sodium met en évidence.
Fe2+ est un réducteur. S2O82- est un oxydant. Quand on mélange des ions Fe2+ et des ions peroxodisulfate S2O82- il se produit une réaction d’oxydoréduction.
Fe2+ est un réducteur. MnO4– est un oxydant. Quand on mélange des ions Fe2+ et des ions permanganate MnO4– il se produit une réaction d’oxydoréduction.
1.2. Écrire les équations des réactions modélisant les transformations chimiques mettant en jeu :
- les ions Fe2+ et les ions S2O82- d’une part,
- les ions Fe2+ et les ions MnO4– d’autre part.
Équation de réaction entre les ions Fe2+ et les ions S2O82-:
Fe3+/Fe2+ : ${\rm Fe}{(aq)}^{2+}={\rm Fe}{(aq)}^{3+}+\operatorname{e}^-\ \ \ \times\mathbf{2}$
S2O82-/SO42- : ${\operatorname{S}_2\operatorname{O}}_{8(aq)}^{2-}+2\operatorname{e}^-=2{{\rm \operatorname{SO}}_4}{(aq)}^{2-}$
${\operatorname{S}_2\operatorname{O}}_{8(aq)}^{2-}+2{\rm Fe}{(aq)}^{2+}\rightarrow2{{\rm \operatorname{SO}}_4}{(aq)}^{2-}+2{\rm Fe}{(aq)}^{3+}$
Équation de réaction entre les ions Fe2+ et les ions MnO4– :
Fe3+/Fe2+ : ${\rm Fe}{(aq)}^{2+}={\rm Fe}{(aq)}^{3+}+\operatorname{e}^-\ \ \ \times\mathbf{5}$
MnO4–/Mn2+ : ${\rm MnO}_{4(aq)}^-+5\operatorname{e}^-+8\operatorname{H}^+={\rm Mn}{(aq)}^{2+}+4\operatorname{H}_2\operatorname{O}{(l)}$
${\rm MnO}_{4(aq)}^-+5{\rm Fe}{(aq)}^{2+}+8\operatorname{H}^+\rightarrow{\rm Mn}{(aq)}^{2+}+5{\rm Fe}{(aq)}^{3+}+4\operatorname{H}_2\operatorname{O}{(l)}$
1.3. Montrer, en vous référant à la couleur de chaque solution titrante, qu’il est plus judicieux de choisir la solution de permanganate de potassium pour réaliser le titrage des ions ferreux contenus dans le produit phytosanitaire, la coloration due aux ions ferreux (Fe2+) ou ferrique (Fe3+) en solution aqueuse étant très peu perceptible.
Les ions peroxodisulfate ${\operatorname{S}2\operatorname{O}}{8(aq)}^{2-}$ n’absorbent quasiment pas dans le visible : Ils ont incolore.

| Équation de réaction entre les ions Fe2+ et les ions S2O82- : | ${\operatorname{S}_2\operatorname{O}}_{8(aq)}^{2-}$ | +2${\rm Fe}{(aq)}^{2+}$ | $\rightarrow2{{\rm \operatorname{SO}}_4}{(aq)}^{2-}$ | +2${\rm Fe}{(aq)}^{3+}$ |
| Couleur | incolore | Vert à peine perceptible | incolore | Rouille à peine perceptible |
Lors de la réaction entre les ions Fe2+ et les ions S2O82- , aucun changement de couleur n’est perceptible.
Les ions permanganate ${\rm MnO}_{4(aq)}^-$ absorbent autour de 530 nm.
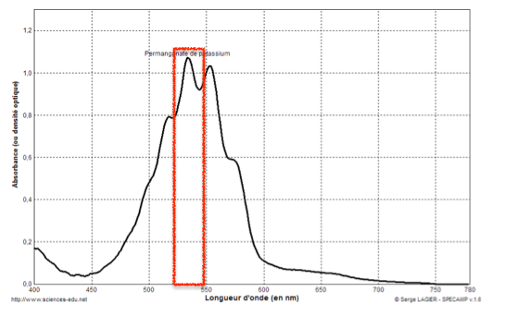
La couleur des ions permanganate ${\rm MnO}_{4(aq)}^-$ est la couleur complémentaire : Magenta
| Équation de réaction entre les ions Fe2+ et les ions MnO4– | ${\rm MnO}_{4(aq)}^-$ | $+ 5{\rm Fe}{(aq)}^{2+}$ | +8$\operatorname{H}^+$ | $\rightarrow{\rm Mn}{(aq)}^{2+}$ | $+5{\rm Fe}{(aq)}^{3+}$ | +4$\operatorname{H}_2\operatorname{O}{(l)}$ |
| Couleur | Magenta | Vert à peine perceptible | incolore | incolore | Rouille à peine perceptible | incolore |
Les ions permanganate sont les seuls à être colorés. Lors d’un titrage, le changement de couleur due à leur présence est perceptible. L’équivalence pourra être repéré grâce au changement de couleur.
Ainsi, il est plus judicieux de choisir la solution de permanganate de potassium pour réaliser le titrage des ions ferreux contenus dans le produit phytosanitaire.
1.4. Définir l’équivalence d’un titrage.
On atteint l’équivalence, lorsqu’on a réalisé un mélange stœchiométrique des deux réactifs qui sont alors totalement consommés.
A L’équivalence, il y’a changement du réactif limitant.
2. Mise en œuvre du titrage

2.1. La solution de permanganate de potassium étant trop concentrée, il est nécessaire de la diluer 5 fois avant de l’utiliser pour le titrage. Choisir, dans la liste de matériel proposé (photographie ci-dessus), la verrerie adaptée à cette dilution. Justifier.
Pour prélever le volume de la solution mère, on utilise une pipette jaugée. Le volume de la solution fille est celui de la fiole jaugée.
On dilue 5 fois la solution S0 pour obtenir une solution S1.
Le volume V1 de la solution fille est 5 fois plus grand que le volume V0 prélevé de la solution mère : V1 =5 V0
Ainsi il faut une fiole jaugée de volume 5 fois supérieur à celui de la pipette jaugée :
On choisit donc une pipette jaugée de 10,0 mL et une fiole jaugée de 50,0 mL et un bécher pour verser la solution mère pour le prélèvement.
Protocole :
- Verser dans un bécher la solution mère
- Prélever à l’aide d’une pipette jaugée 10,0 mL
- Introduire ce volume dans une fiole jaugée de 50,0 mL
- Compléter jusqu’au trait de jauge avec de l’eau distillée
- Homogénéiser la solution
2.2. Expliquer pourquoi certaines verreries sont associées à des capacités notées 100 mL, 50 mL, 10 mL, et d’autres à des capacités de 100,0 mL, 50,0 mL, 10,0 mL.
Certaines verreries associées à des capacités notées 100 mL, 50 mL, 10 mL, sont moins précises que d’autres à des capacités de 100,0 mL, 50,0 mL, 10,0 mL.
2.3. Le produit phytosanitaire se présente sous la forme d’une poudre. Afin de réaliser le titrage, on dissout 100,0 g de produit dans de l’eau et on complète avec de l’eau de façon à obtenir 1,0 L de solution.
2.3.1. On prélève 10,0 mL de cette solution qu’on introduit dans un erlenmeyer. Dans la liste de matériel proposée ci-dessus, choisir la verrerie utilisée pour prélever ces 10,0 mL.
On prend une pipette jaugée de 10,0 mL pour prélever.
2.3.2. Schématiser et légender le montage utilisé afin de réaliser le titrage.
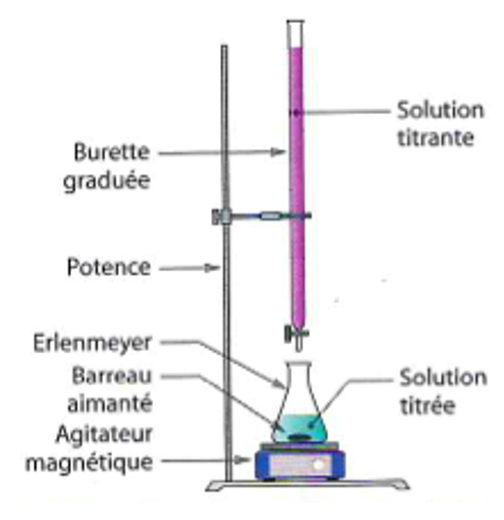
3. Exploitation du résultat du titrage
3.1. Le titrage est réalisé plusieurs fois. On note VE, le volume de solution de permanganate de potassium versé pour atteindre l’équivalence pour chaque titrage réalisé. Les résultats sont rassemblés dans le tableau suivant :
| Mesure | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| VE en mL | 11,0 | 10,6 | 10,4 | 10,6 | 10,8 | 10,5 | 10,7 | 10,9 | 11,2 | 11,0 |
3.1.1. L’incertitude-type u(VE), de type A, sur cette série de mesures est égale à 0,080 mL. Écrire le résultat de la mesure pour VE.
Calculons la valeur moyenne :
$\operatorname{V}_E=\frac{11,0+10,6+10,4+10,6+10,8+10,5+10,7+10,9+11,2+11,0}{10}$
$\operatorname{V}_E=10,77\ mL$
Exprimons ce résultat avec l’incertitude :
$\operatorname{V}_E=10,77\pm0,080\ \ mL$
3.1.2. Une autre méthode de détermination de l’incertitude-type sur le volume équivalent aurait pu être prise en compte. Préciser sa nature.
L’incertitude de type B. Incertitude estimée à partir des incertitudes sur les instruments et les solutions utilisées.
3.1.3. Déterminer la teneur en masse d’ions ferreux présente dans l’échantillon de 10,0 mL de solution titrée prélevé.
Déterminer la teneur en masse : déterminer le pourcentage massique.
${\rm MnO}_{4(aq)}^-+5{\rm Fe}{(aq)}^{2+}+8\operatorname{H}^+\rightarrow{\rm Mn}{(aq)}^{2+}+5{\rm Fe}{(aq)}^{3+}+4\operatorname{H}_2\operatorname{O}{(l)}$
A l’équivalence :
$\frac{\operatorname{n}_{{\rm Fe}^{2+}}^i}{5}=\frac{\operatorname{n}_{{\rm MnO}_4^-}^{eq}}{1}$
$\operatorname{n}_{{\rm Fe}^{2+}}^i=5{\times\operatorname{n}}_{{\rm MnO}_4^-}^{eq}$
Or $n=c\times V$ et $n=\frac{\operatorname{m}}{M}$
$\frac{\operatorname{m}{{\rm Fe}^{2+}}}{\operatorname{M}_{{\rm Fe}^{2+}}}=5\times\left[{\rm MnO}_4^-\right]\times\operatorname{V}_E$
$\operatorname{m}_{{\rm Fe}^{2+}}=5\times\left[{\rm MnO}_4^-\right]\times\operatorname{V}_E\times\operatorname{M}_{{\rm Fe}^{2+}}$
$\operatorname{m}_{{\rm Fe}^{2+}}=5\times\left(\frac{0,10}{5}\right)\times10,77.{10}^{-3}\times56,0=0,060\ g$
Cette masse est celle contenue dans les 10,0 mL dosés.
| 0,060 g | 10,0 mL |
| m | 1,0 L |
$m=\frac{1,0\times0,060}{10,0\times{10}^{-3}}$
$m=6,0\ g$
Soit une masse de 6,0 g dans un litre.
Dans la question 2.3 : « on dissout 100,0 g de produit dans de l’eau et on complète avec de l’eau de façon à obtenir 1,0 L de solution. » Ainsi $\operatorname{m}_{Totale}=100,0\ g$.
Calculons la teneur ou le pourcentage massique :
$P=\frac{\operatorname{m}}{\operatorname{m}_{Totale}}$
$P=\frac{6,0}{100,0}=0,060=6,0%$
Le résultat correspond à l’indication de l’emballage.
3.2. Un titrage par spectrophotométrie peut-il être adapté au contrôle de la teneur en fer du produit phytosanitaire indiquée sur l’emballage ?
Pour réaliser un titrage par spectrophotométrie, il faut que :
- L’ion Fe2+ ai un spectre A=f(λ) qui présente un maximum d’absorption dans le domaine UV-visible. D’après le tableau des données, l’ion Fe2+ est de couleur vert à peine perceptible. Cette condition est vérifiée.
- Que l’ion Fe2+ soit le seul qui absorbe pour cette longueur d’onde dans le mélange.
Si ces conditions sont réunies, un titrage par spectrophotométrie peut être adapté au contrôle de la teneur en fer du produit phytosanitaire indiquée sur l’emballage.
