E3C2 – 10 points – Durée 1h – calculatrice autorisée
Sujet n°G1SPHCH02695, n°G1SPHCH02762 et n°G1SPHCH02776
Télécharger l’exercice en PDF :
L’objet de l’exercice est de proposer un modèle pour l’étude du mouvement d’une balle de tennis.
Données :
- intensité de la pesanteur : g = 9,8 N/kg ;
- masse volumique de l’air à 20 °C : ρ = 1,0.10-6 kg/cm3 ;
- le diamètre des balles de tennis est en moyenne de 6,5 cm.
1. Modélisation de la chute verticale de la balle
Une balle, de masse m = 55 g, est lâchée sans vitesse initiale. On filme ce mouvement de chute verticale et, à l’aide d’un logiciel adapté, on relève les positions successives de la balle. Un programme informatique permet de calculer les énergies cinétiques, potentielles de pesanteur et mécaniques de la balle à partir des relevés.
L’origine du repère est prise au sol, et l’axe des altitudes est dirigé vers le haut. On note A la position initiale de la balle lorsqu’elle quitte la main de l’opérateur, et B son point d’impact, sur le sol.

1.1. On identifie trois forces qui peuvent s’exercer sur la balle lors de son mouvement :
- le poids $\overrightarrow{P}$ de la balle ;
- la force de frottement $\overrightarrow{f}$ exercée par l’air sur la balle et qui dépend de la vitesse de la balle ;
- la poussée d’Archimède $\overrightarrow{F_A}$, indépendante de la vitesse de la balle, qui est exercée par l’air sur la balle, dirigée vers le haut et de valeur FA=ρ×g×V , avec V le volume de la balle et ρ la masse volumique de l’air.
Représenter sur votre copie un schéma de la balle modélisée par un point en M, à un instant quelconque de son mouvement ainsi que les forces s’exerçant sur elle, sans souci d’échelle.
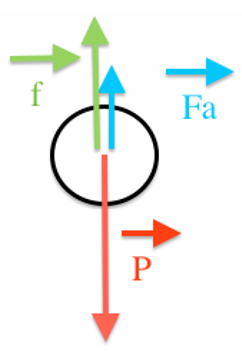
1.2. Comparer la valeur de la poussée d’Archimède au poids et en déduire que la poussée d’Archimède est négligeable devant le poids.
Pour comparer nous faisons le rapport
$\frac{\operatorname{P}}{\operatorname{F}_A}=\frac{m\times\operatorname{g}}{\rho\times\operatorname{g}\times\operatorname{V}}=\frac{\operatorname{m}}{\rho\times\operatorname{V}}$
$V=\frac{4}{3}\times\pi\times\operatorname{r}^3$
$\frac{\operatorname{P}}{\operatorname{F}_A}=\frac{\operatorname{m}}{\rho\times\frac{4}{3}\times\pi\times\operatorname{r}^3}=\frac{55.10^{-3}}{1,0.10^{-6}\times\frac{4}{3}\times\pi\times(\frac{6,5}{2})^3}=382$
FA est négligeable devant P
1.3. Parmi les trois séries de points reproduites sur la figure ci-après, identifier en justifiant la réponse :
- la série de points qui correspond aux mesures de l’énergie cinétique ;
- la série de points qui correspond aux mesures de l’énergie potentielle de pesanteur ;
- la série de points qui correspond aux mesures de l’énergie mécanique.
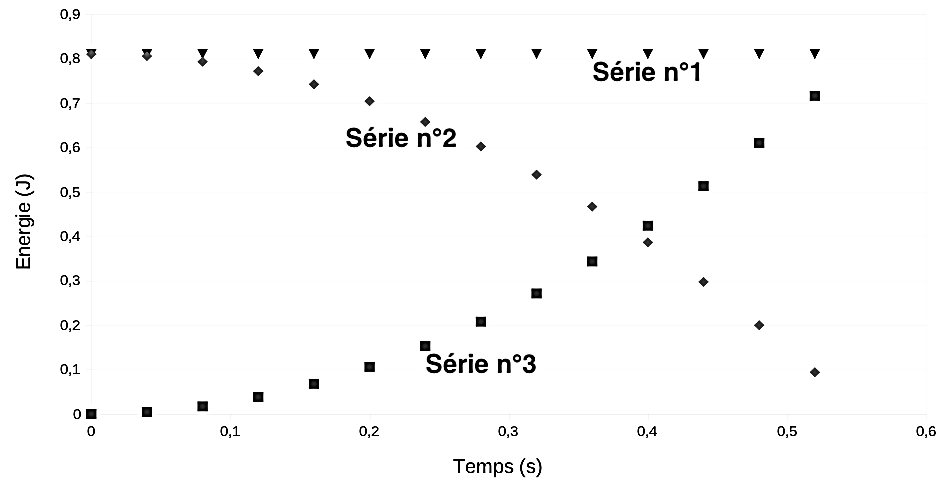
L’énergie cinétique : $\operatorname{E}_c=\frac{1}{2}m.\operatorname{v}^2$. Lors de la chute de la balle, la vitesse augmente donc Ec augmente. Cela correspond à la série n°3
L’énergie potentielle de pesanteur Epp=mgz. Lors de la chute de la balle, l’altitude diminue donc Epp diminue. Cela correspond à la série n°2
L’énergie mécanique EM=EC+Ep. L’énergie mécanique est la somme des énergies cinétique et potentielle. Cela correspond à la série n°1
1.4. À l’aide de ces courbes, justifier que l’on peut, dans cette étude, faire le choix de négliger les forces de frottement.
L’énergie mécanique (série n°1) ne varie pas lors de la chute elle se conserve : Em=constante.
Ainsi les forces de frottements sont négligeables.
1.5. À quelle force est due la variation d’énergie cinétique observée ? Donner la valeur de son travail sur le trajet AB.
La seule force qui s’exerce est le poids car la force de frottement est négligeable ( question 1.4) , la poussée d’Archimède est négligeable ( question 1.2).
Le poids est responsable de la variation d’énergie cinétique observée.
Calculons le travail du poids sur le trajet AB :
Théorème de l’énergie cinétique :
$\Delta\operatorname{E}_C=\Sigma\operatorname{W}_{AB}(\overrightarrow{F})$
$\operatorname{E}_{C\ (B)}-\operatorname{E}_{C\ (A)}=\operatorname{W}_{AB}\left(\overrightarrow{P}\right)$
$\operatorname{W}_{AB}\left(\overrightarrow{P}\right)=\operatorname{E}_{C\ \left(B\right)}-\operatorname{E}_{C\ \left(A\right)}$
Par lecture graphique : $\operatorname{E}_{C\ \left(B\right)}=0,08J\ et\ \operatorname{E}{C\ \left(A\right)}=0J$
$\operatorname{W}_{AB}\left(\overrightarrow{P}\right)=0,8-0=0,8\ J$
2. Modélisation du service au tennis
L’objectif de cette seconde partie est de vérifier si le modèle proposé dans la première partie convient aussi pour le mouvement de la balle lors du service, c’est-à-dire une fois qu’elle a quitté la raquette, venant d’être frappée par le joueur qui engage. Pour la suite de l’exercice, toutes les forces sont négligées, sauf le poids.

La position initiale de la balle est notée C, lieu où le contact est rompu avec la raquette. La vitesse de la balle en C, supposée horizontale, est notée $\overrightarrow{v_C}$. Son altitude est notée zC. Le schéma de la situation est représenté ci-dessous sans souci d’échelle. La balle atteint le sol au point D, à la vitesse de norme vD et à la même altitude que l’origine du repère choisi.
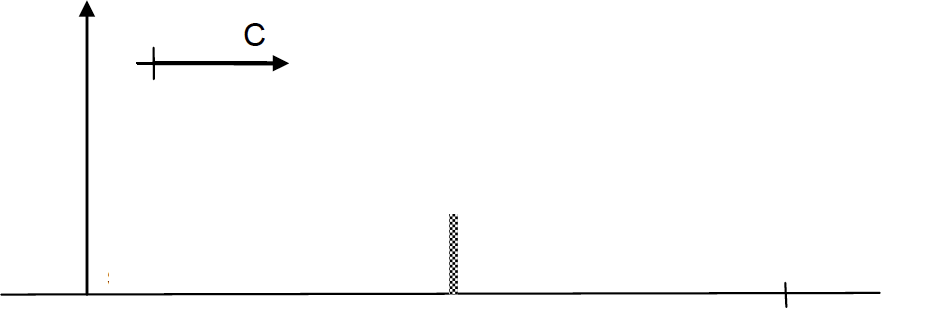
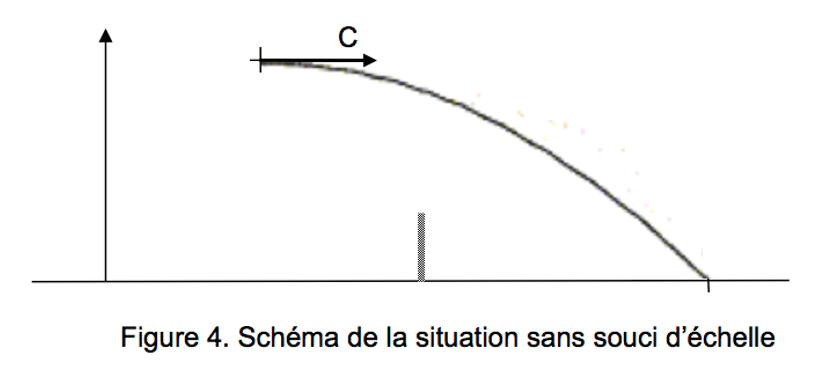
2.1. Reproduire la figure 4 et le compléter en représentant l’allure de la trajectoire de la balle lors du service.
2.2. Montrer à l’aide d’un théorème énergétique que, dans les conditions du modèle proposé dans la première partie, la vitesse au point d’impact s’écrit : $v_D=\sqrt{v_C^2+2\times g\times z_C} $
Méthode 1 : Théorème de l’énergie cinétique :
$\Delta\operatorname{E}_C=\Sigma\operatorname{W}_{AB}(\overrightarrow{F})$
$\operatorname{E}_{C\ finale}-\operatorname{E}_{C\ initiale}=\Sigma\operatorname{W}_{AB}(\overrightarrow{P})$
$\operatorname{E}_{C\ \left(D\right)}-\operatorname{E}_{C\ \left(C\right)}=m\times g\ \times\left(\operatorname{Z}C-\operatorname{Z}D\right)$
$\frac{1}{2}m\operatorname{v}\operatorname{D}^2-\frac{1}{2}m\operatorname{v}\operatorname{C}^2=m\times g\ \times\left(\operatorname{Z}_C-\operatorname{Z}_D\right)$
Or ZD=0 m car au sol
$\frac{1}{2}m\operatorname{v}_\operatorname{D}^2-\frac{1}{2}m\operatorname{v}_\operatorname{C}^2=m\times g\ \times\operatorname{Z}_C$
$\frac{1}{2}m\operatorname{v}_\operatorname{D}^2=m\times g\ \times\operatorname{Z}_C+\frac{1}{2}m\operatorname{v}_\operatorname{C}^2$
$\operatorname{v}_\operatorname{D}^2=\frac{2}{m}(m\times g\ \times\operatorname{Z}_C+\frac{1}{2}m\operatorname{v}_\operatorname{C}^2)$
$\operatorname{v}_\operatorname{D}^2=2\times g\ \times\operatorname{Z}_C+\operatorname{v}_\operatorname{C}^2$
$\operatorname{v}_D=\sqrt{2\times g\ \times\operatorname{Z}_C+\operatorname{v}_\operatorname{C}^2}$
Méthode 2 : Théorème de l’énergie mécanique :
$\Delta\operatorname{E}_m=\Sigma\operatorname{W}_{AB}(\overrightarrow{F}_{non\ conservatives})$
$\operatorname{E}_{m\ \left(D\right)}-\operatorname{E}_{m\ \left(C\right)}=0$
$\operatorname{E}_{C\ \left(D\right)}+\operatorname{E}_{pp\ \left(D\right)}-\left(\operatorname{E}_{C\ \left(C\right)}+\operatorname{E}_{pp\ \left(C\right)}\right)=0$
$\operatorname{E}_{C\ \left(D\right)}+\operatorname{E}_{pp\ \left(D\right)}-\operatorname{E}_{C\ \left(C\right)}-\operatorname{E}_{pp\ \left(C\right)}=0$
$\frac{1}{2}m\operatorname{v}_\operatorname{D}^2+m\times g\ \times\operatorname{Z}_D-\frac{1}{2}m\operatorname{v}_\operatorname{C}^2-m\times g\ \times\operatorname{Z}_C=0$
Or ZD=0 m car au sol
$\frac{1}{2}m\operatorname{v}_\operatorname{D}^2-\frac{1}{2}m\operatorname{v}_\operatorname{C}^2-m\times g\ \times\operatorname{Z}_C=0$
$\frac{1}{2}m\operatorname{v}_\operatorname{D}^2=\frac{1}{2}m\operatorname{v}_\operatorname{C}^2+m\times g\ \times\operatorname{Z}C$
$\operatorname{v}_\operatorname{D}^2=\frac{2}{m}\times\left(\frac{1}{2}m\operatorname{v}_\operatorname{C}^2+m\times g\ \times\operatorname{Z}_C\right)$
$\operatorname{v}_\operatorname{D}^2=2\times g\ \times\operatorname{Z}_C+\operatorname{v}_\operatorname{C}^2$
$\operatorname{v}_D=\sqrt{2\times g\ \times\operatorname{Z}_C+\operatorname{v}_\operatorname{C}^2}$
2.3. Déterminer la valeur de vD pour zC = 2,20 m et vC = 200 km.h-1 pour ce modèle. Commenter.
$\operatorname{v}_D=\sqrt{2\times9,8\times2,2+(\frac{200}{3,6})^2}=56\ m.\operatorname{s}^{-1}\ soit\ 201km.\operatorname{h}^{-1}$
La valeur est très grande pour une balle de tennis.
2.4. Avec les valeurs initiales précédentes, la valeur de la vitesse vDexp effectivement mesurée au point D est de l’ordre de 100 km.h-1. Proposer une hypothèse qui pourrait expliquer l’écart entre les valeurs de la vitesse mesurée et de celle déterminée avec le modèle précédent.
Dans le modèle précèdent, nous avons considéré que toutes les forces sont négligées, sauf le poids.
Nous devons prendre en compte les forces de frottements pour que la valeur trouvée se rapproche de la valeur mesurée.
