E3C2 – 10 points – Durée 1h – calculatrice autorisée
Sujet n°G1SPHCH02717, n°G1SPHCH02731 et n°G1SPHCH02750
Télécharger l’exercice en PDF :
Les « biocarburants » sont des carburants obtenus à partir de la biomasse (matière première d’origine végétale, animale ou issue de déchets). Mélangés avec les carburants traditionnels, leur utilisation dans le secteur des transports a pour but de répondre à cinq enjeux essentiels :
- réduire les émissions de gaz à effet de serre,
- anticiper l’épuisement des réserves mondiales de pétrole,
- réduire la dépendance énergétique pétrolière,
- offrir un débouché supplémentaire aux filières agricoles,
- créer une filière de valorisation des déchets.
Il existe actuellement deux filières principales :
- La filière éthanol, pour les véhicules essence,
- La filière huile et dérivés pour les véhicules diesel.
D’après https://www.ecologique-solidaire.gouv.fr/biocarburants
Ce sujet s’intéresse à la valorisation de la biomasse sous la forme de biocarburant en étudiant une des filières de valorisation des déchets générés par la synthèse de biodiésel et en comparant la combustion d’une essence classique et de bioéthanol.
Données :
- Masses molaires moléculaires :
Glycérol M = 92,09 g.mol–1 1,2,3-triméthoxypropane M = 134,2 g.mol–1
- Table de données spectroscopiques Infrarouge
1. Valorisation du glycérol
Les biodiesels sont obtenus à partir d’huile végétale ou animale subissant une transformation chimique appelée transestérification, modélisée par une réaction, dont l’équation figure ci-dessous, entre les triglycérides contenus dans les matières grasses et le méthanol. Les groupes alkyles comportant de longues chaînes carbonées sont notés R.
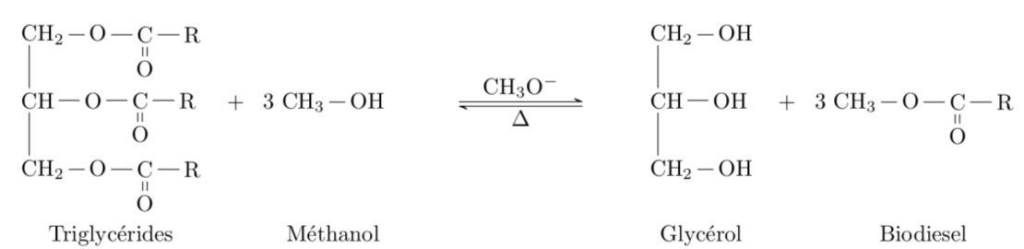
D’après https://www.irsst.qc.ca/media/documents/PubIRSST/B-079.pdf
1.1. Justifier le nom de l’alcool réagissant avec les triglycérides.
- méthan : 1 carbone
- ol : famille des alcools, présence d’un groupe hydroxyle OH
1.2. La transestérification étant une transformation totale, quelle doit être la relation entre les quantités de matière de triglycérides et de méthanol introduits pour que les triglycérides soient entièrement transformés en biodiesel ?
Il faut que les réactifs soient introduits en proportions stœchiométriques :
$$\frac{n_{triglycérides}^i}{1}=\frac{n_{méthanol}^i}{3}$$
Les normes européennes imposent une utilisation croissante de biocarburants dans le secteur des transports. Des voies pour la valorisation du glycérol, produit secondaire de la réaction, sont donc activement recherchées par les chimistes. Celui-ci est déjà utilisé dans de nombreux domaines industriels : médicaments, cosmétiques ou alimentation, par exemple. Parmi les voies de valorisation du glycérol, la conversion en acroléine et surtout en acide acrylique sont particulièrement prometteuses.
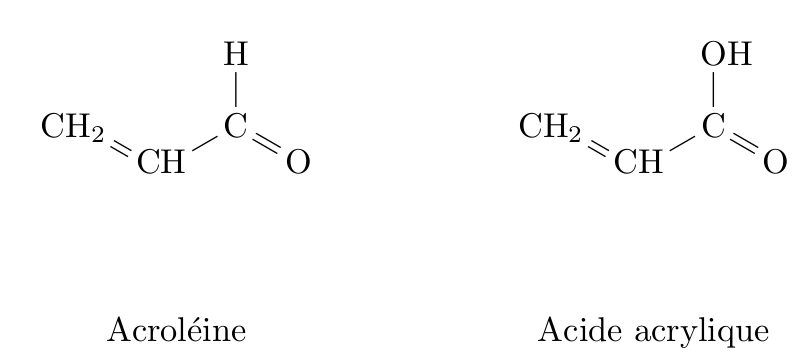
1.3. Reproduire les formules semi-développées de l’acroléine et de l’acide acrylique sur votre copie et entourer les groupes caractéristiques. Nommer la famille de composés associée à chaque groupe.
Acroléine
Groupe : Carbonyle
Famille : Aldéhyde
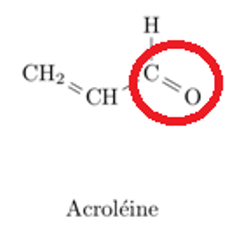
Acide acrylique
Groupe : Carboxyle
Famille : Acide carboxylique
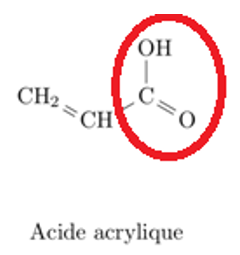
1.4. Montrer que la transformation du glycérol en acroléine peut être modélisée par une réaction de déshydratation.
Glycérol : C3H8O3
Acroléine : C3H4O
Entre le glycérol : C3H8O3 et l’acroléine : C3H4O, il y’a une différence de 4H et 2O soit 2 molécules d’eau H2O
Ainsi on peut modéliser la transformation du glycérol en acroléine par la réaction de déshydratation suivante : C3H8O3 → C3H4O + 2 H2O
1.5. Montrer que lors de la transformation de l’acroléine en acide acrylique, l’acroléine subit une oxydation. Une demi-équation électronique est attendue.
Acroléine : C3H4O
Acide acrylique : C3H4O2
C3H4O + H2O =C3H4O2 + 2H+ + 2e–
Ainsi l’acroléine perd des électrons, il subit une oxydation.
2. Étude de la combustion d’un biocarburant
Depuis 2010, la quasi-totalité des stations essences aux États-Unis proposent une essence sans plomb contenant 10% de bioéthanol ; c’est aussi le cas en Europe avec le SP95-E10 Un carburant encore plus riche en éthanol, le E85, contenant 65 à 85% d’éthanol issu de la culture de la canne à sucre, de la betterave ou du maïs par exemple, déjà largement utilisé au Brésil, commence à se répandre aussi en Europe et aux États-Unis. Cependant, le moteur, pour accepter ce type de carburant, nécessite un réglage de l’avance à l’allumage et du débit des injecteurs car le volume de carburant à injecter est supérieur à celui d’un carburant classique pour une même quantité d’air.
D’après Markov, Sergei. (2012). Biofuels and Synthetic Fuels.
https://fr.wikipedia.org/wiki/E85_(carburant)
L’essence sans plomb 95 est modélisée par du 2,2,4-triméthylpentane pur de masse molaire M1 = 114 g.mol-1 et de masse volumique ρ1=690 g.L-1 et le E85 par de l’éthanol pur de masse molaire M2 = 46 g.mol-1 et de masse volumique ρ2=789 g.L-1.
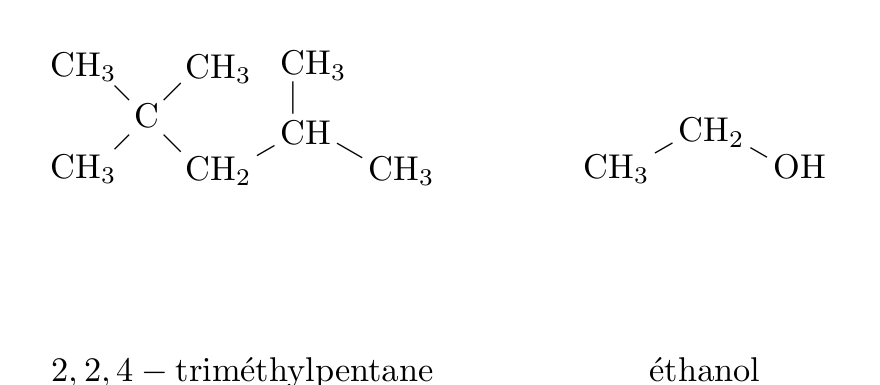
La combustion du 2,2,4-triméthylpentane dans le dioxygène est modélisée par la réaction d’équation écrite ci-dessous. C’est une transformation totale.
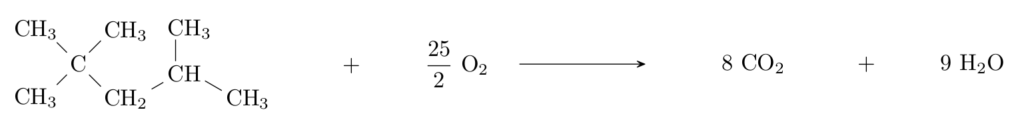
Le programme python reproduit ci-dessous permet de calculer et d’afficher l’état final du système et l’avancement final de la réaction de combustion de 2,0 moles de 2,2,4-triméthylpentane avec 5,0 moles de dioxygène.
1 especes = [« 2,2,4-trimethylpentane », »O2″, »CO2″, »H2O »]
2 coefficients = [-1, -25/2, 8, 9]
3 qi = [2., 5., 0., 0.] # Quantités de matières initiales en moles
4 qf = qi[:] # Quantités de matière à l’instant t = 0
5 # identiques aux quantités initiales
6 pas = 0.00001 #Pas de la simulation en moles
7
8 x = 0 # Avancement initial en moles
9 while qf[0] > 0 and qf[1] > 0: # Tant que la condition est vraie
10 x = x + pas # L’avancement augmente de la valeur du pas
11 for i in range(4): # Pour chacune des 4 espèces
12 qf[i] = qi[i] + coefficients[i] * x # Calcul des nouvelles quantités de matière
13
14 print(« ====== Etat Final ====== »)
15 for i in range(4): # Pour chacune des 4 espèces
16 print(« {} : {:.3f} ».format(especes[i], qf[i])) # On affiche la quantité de
17
18 # matière à l’état final avec 3
19 # chiffres après la virgule
20 print(« Avancement final : xf = {:.3f} mol ».format(x)) # On affiche l’avancement final
21 # avec 3 chiffres
22 # après la virgule
Sortie :
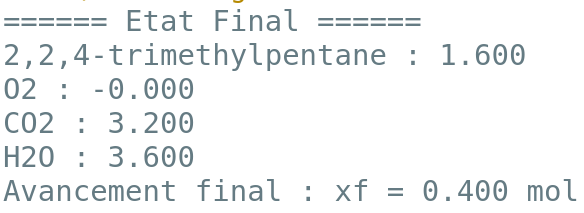
2.1. Lors de la combustion du 2,2,4-triméthylpentane, décrire qualitativement l’évolution des quantités de matière des différentes espèces chimiques au cours de la transformation. Comment le programme python prend-t-il en compte cette différence de comportement entre les réactifs et les produits ?
Les quantités de matière des réactifs (2,2,4-triméthylpentane et dioxygène) diminuent.
Les quantités de matière des produits (dioxyde de carbone et eau) augmentent.
Le programme python prend en compte cette différence de comportement entre les réactifs et les produits en donnant des coefficients négatifs aux réactifs et positifs aux produits (ligne 2 : coefficients = [-1, -25/2, 8, 9] )
2.2. A partir de l’état final affiché par le programme, déterminer, sans calcul, le réactif limitant dans les conditions de la simulation. A quelle ligne du programme python détermine-t-on que la transformation est achevée ?
Dans l’état final en sortie du programme, la quantité de O2 est à Zéro : c’est le réactif limitant.
Dès que l’une des quantités de matière des réactifs est nulle, la transformation est achevée, la boucle se termine (ligne 9) et l’état final peut être affiché (ligne 14).
2.3. Écrire et ajuster la réaction de combustion de l’éthanol dans le dioxygène.
$$\operatorname{C}_2\operatorname{H}_6O+3\operatorname{O}_2\rightarrow{2\operatorname{CO}}_2+{3\operatorname{H}}_2O$$
2.4. Indiquer, puis réécrire les lignes à modifier dans le programme python pour calculer l’état final de la réaction de combustion de 5,0 moles d’éthanol avec 10,0 moles de dioxygène.
Il faut modifier les 3 premières lignes (modifications en bleu) :
| 1 2 3 | especes = [« éthanol« , »O2″, »CO2″, »H2O »] coefficients = [-1, -3, 2, 3] qi = [5., 10., 0., 0.] # Quantités de matières initiales en moles |
On donne les sorties du programme pour la réaction de combustion d’1 mole de carburant dans 1 mole de dioxygène pour les deux modèles de carburants considérés.
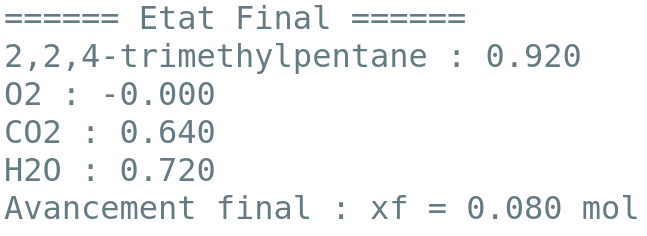
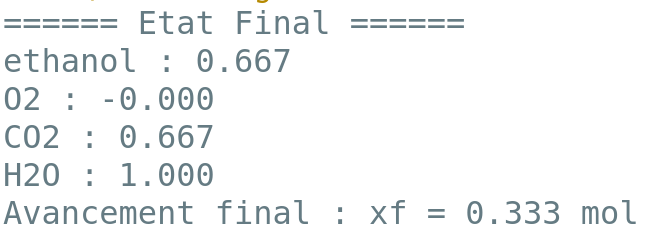
2.5. D’après les sorties des programmes et vos calculs, la phrase en italique de l’introduction de la partie 2 vous paraît-elle justifiée ? Vous porterez un regard critique sur les résultats obtenus.
Toute démarche de résolution sera valorisée même si elle n’a pas abouti.
Phrase en italique : « le volume de carburant à injecter est supérieur à celui d’un carburant classique pour une même quantité d’air. »
Pour être dans les proportions stœchiométriques :
1ère équation :
$$\frac{n_{2,2,4-trimethylpentane}}{1}=\frac{n_{O_2}}{25/2}$$
$$n_{O_2}=\frac{25}{2}n_{2,2,4-trimethylpentane}$$
2nd équation :
$$\frac{n_{éthanol}}{1}=\frac{n_{O_2}}{3}$$
$$n_{O_2}=3n_{éthanol}$$
Or nous devons comparer les volumes de carburant pour une même quantité d’air donc de O2 :
$$3n_{éthanol}=\frac{25}{2}n_{2,2,4-trimethylpentane}$$
Or $$n=\frac{m}{M}$$
soit :
$$\frac{3\times m_{éthanol}}{M_{éthanol}}=\frac{25}{2}\times\frac{m_{2,2,4-trimethylpentane}}{M_{2,2,4-trimethylpentane}}$$
Or
$$m=\rho\times V$$
D’ou :
$$\frac{3\times\rho_{éthanol}\times V_{éthanol}}{M_{éthanol}}=\frac{25}{2}\times\frac{\rho_{2,2,4-trimethylpentane}\times V_{2,2,4-trimethylpentane}}{M_{2,2,4-trimethylpentane}}$$
Isolons Véthanol :
$$V_{éthanol}=\frac{25}{2}\times\frac{\rho_{2,2,4-trimethylpentane}\times V_{2,2,4-trimethylpentane}}{M_{2,2,4-trimethylpentane}}\times\frac{1}{3}\times\frac{M_{éthanol}}{\rho_{éthanol}}$$
Remplaçons\ \rho et M par leurs valeurs :
$$V_{éthanol}=\frac{25}{2}\times\frac{690\times V_{2,2,4-trimethylpentane}}{114}\times\frac{1}{3}\times\frac{46}{789}$$
$$V_{éthanol}=1,47\times V_{2,2,4-trimethylpentane}$$
On en déduit que pour une même quantité d’air, le de carburant à injecter est supérieur à celui d’un carburant classique. La phrase en italique est justifiée.
Critique : le programme compare les deux réactions pour une même quantité de matière de carburant. Or la phrase en italique compare les volumes de carburant. Les deux carburants n’ayant pas la même masse volumique, les résultats obtenus par le programme ne sont pas exploitables pour notre comparaison.
