Lunette astronomique et observation de mars

Centres étrangers 2022 Sujet 1

Exercice 1– (10 points) –  Commun à tous les candidats – Durée 1h45 – Calculatrice autorisée

Sujet n° 22-PYCJ1G11

Un astronome amateur vient d’acquérir une lunette astronomique avec l’intention d’observer la calotte polaire Nord de la planète Mars.


Mars le 30/10/2020
https://blogs.futura-sciences.com/

Cette lunette est dotée d’un objectif de distance focale 910 mm et d’un oculaire de distance focale 20 mm.

Les objectifs de cet exercice sont :

  • Déterminer la distance maximale Terre-Mars pour pouvoir observer cette calotte polaire à travers la lunette (Partie A) ;
  • Estimer le temps de mise en température de la lunette pour optimiser les conditions d’observation (Partie B).

Les deux parties peuvent être traitées indépendamment.

Partie A – Distance maximale Terre-Mars permettant d’observer la calotte polaire Nord

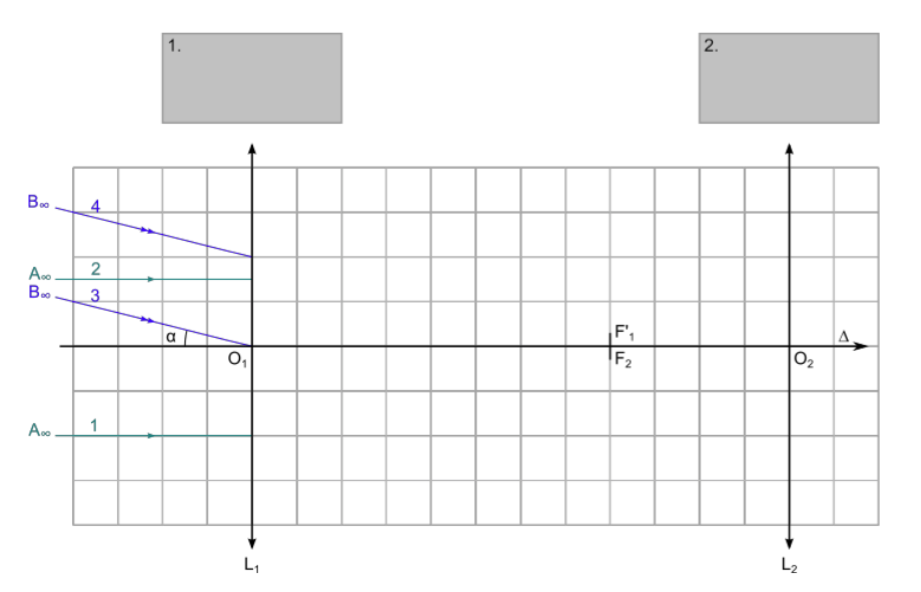
La lunette astronomique étudiée est afocale. Elle est modélisée sur un banc optique par deux lentilles minces convergentes L1 et L2 (voir figure en ANNEXE page 15/15 à rendre avec la copie) placées de telle sorte que le foyer image F’1 de la lentille L1 coïncide avec le foyer objet F2 de la lentille L2.

On cherche à former l’image à travers la lunette d’un objet 𝐴∞𝐵∞ situé « à l’infini ». Le point 𝐴∞ est sur l’axe optique, le point 𝐵∞ est hors axe optique.

  • Les rayons issus de 𝐴∞ arrivent sur la lunette parallèlement à l’axe optique.
  • Les rayons issus de 𝐵∞ arrivent sur la lunette parallèles entre eux, avec une inclinaison 𝛼 par rapport à l’axe optique.

L’angle 𝛼 est l’angle sous lequel est vu l’objet 𝐴∞𝐵∞ à l’œil nu. L’angle 𝛼 est donc l’angle entre les rayons issus de 𝐴∞ et les rayons issus de 𝐵∞. On note 𝛼′ l’angle sous lequel on voit l’image 𝐴’𝐵’ de l’objet 𝐴∞𝐵∞ à travers la lunette.

Données :

  • Pouvoir séparateur de l’œil humain : pour pouvoir distinguer deux points 𝐴 et 𝐵, l’angle 𝜃 sous lequel un œil humain les observe doit être supérieur à l’angle 𝜃0 = 2,7 × 10−4 rad (voir figure ci-dessous).
  • Pour un angle 𝜃 petit, tan 𝜃 ≃ 𝜃 , où l’angle 𝜃 est exprimé en radians.
  • Une lunette est dite « afocale » si elle forme une image à l’infini d’un objet situé à l’infini.
  • L’unité astronomique (UA) est une unité de distance qui correspond à la distance moyenne Soleil-Terre.         1 UA = 150 millions de km soit 1,50×1011m.
  • Distance moyenne Soleil-Mars : 1,5 UA.

La lunette modélisée

1. Compléter les cadres 1 et 2 sur le schéma, en ANNEXE page 15/15 à rendre avec la copie, en indiquant les noms spécifiques donnés aux lentilles L1 et L2.

2. Sur le schéma, en ANNEXE page 15/15 à rendre avec la copie, représenter le faisceau émergent issu du point 𝐴∞ délimité par les rayons 1 et 2 et traversant la lunette.

3. Sur le schéma, en ANNEXE page 15/15 à rendre avec la copie, représenter de même le faisceau émergent issu du point 𝐵∞ délimité par les rayons 3 et 4 et traversant la lunette.

4. Sur le schéma, en ANNEXE page 15/15 à rendre avec la copie, faire apparaître l’angle 𝛼′ sous lequel est vue l’image de l’objet à l’infini à travers la lunette ainsi que l’image intermédiaire 𝐴1𝐵1 (c’est-à-dire l’image de 𝐴∞𝐵∞ à travers la lentille L1).

5. Justifier le terme « afocal » pour caractériser cette lunette.

Visibilité de la calotte polaire

6. Rappeler la définition du grossissement 𝐺 de la lunette faisant intervenir 𝛼 et 𝛼’.

7. Montrer que le grossissement de la lunette afocale peut se mettre sous la forme :

G=\frac{f_1^'}{f_2^'}

où 𝑓′ est la distance focale de la lentille L1 et 𝑓′ est la distance focale de la lentille L2. On utilisera l’approximation des petits angles pour les angles 𝛼 et 𝛼’.

On note 𝛼min la valeur minimale que doit avoir l’angle 𝛼 pour que l’objet soit observable par un œil humain à l’aide de cette lunette.

8. Déterminer l’expression de 𝛼min en fonction 𝑓’1 , 𝑓’2 et 𝜃0. Vérifier que, pour la lunette de l’astronome amateur, 𝛼min = 5,9 × 10−6 rad.

9. Sachant que la taille de la calotte polaire Nord de Mars a un diamètre 𝑑 d’environ 103 km, donner une estimation, en km, de la distance maximale 𝐷 entre Mars et la Terre permettant d’observer cette calotte polaire.

La distance Terre-Mars n’est pas constante. Elle varie au cours du temps entre 0,5 et 2,5 unités astronomiques (UA).

10. Compte tenu de la valeur de 𝐷 trouvée à la question 9, préciser si l’astronome amateur pourra finalement observer la calotte polaire Nord de Mars avec sa lunette.

Partie B – Mise en température avant observation

Lors d’une observation astronomique, l’un des problèmes auxquels sont confrontés les astronomes est la turbulence de l’air. Elle apparaît lorsque l’air n’est plus un milieu homogène. La lumière ne se propage alors plus tout-à-fait en ligne droite et l’image de ce que l’on observe est déformée. La turbulence peut avoir plusieurs origines. L’une d’elles est la turbulence instrumentale, qui se produit lorsque l’instrument d’optique utilisé et l’air environnant ne sont pas à la même température. Il est ainsi conseillé de mettre l’instrument « en température », c’est-à-dire de le sortir suffisamment à l’avance sur le site d’observation afin que sa température s’écarte de moins de 1°C de la température de l’air extérieur.

L’astronome cherche à savoir si une durée de deux heures pour la mise en température de son instrument est suffisante pour limiter la turbulence instrumentale.

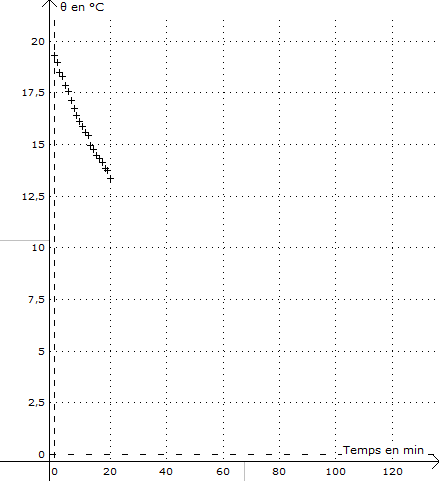
Pour cela, à l’instant t = 0, il met la lunette en contact avec l’air extérieur et mesure sa température pendant 20 minutes à intervalles de temps réguliers. Les résultats sont représentés sur le graphique ci-contre.

Il utilise ensuite une modélisation théorique afin de prédire l’évolution de la température sur des durées plus longues.

Loi de Newton

Le flux thermique Ф entre un système à la température θ et un thermostat à la température

θe est proportionnel à la différence de température (θe – θ).

𝛷 = ℎ 𝑆 (𝜃𝑒 − 𝜃)

  • Ф : flux thermique (W)
  • h : coefficient d’échange thermique (W·m-2·°C-1)
  • S : aire de la surface d’échange entre le corps et le
  • thermostat (m2)
  • θ : température du corps (°C)
  • θe : température du thermostat (°C)

Cette loi modélise correctement les échanges dominés principalement par la convection.

Données :

  • Température initiale de la lunette : 𝜃0 = 19,5 °C à la date t = 0.
  • Température extérieure, supposée constante : 𝜃𝑒 = 9,0 °C.
  • Lorsque un système incompressible au repos subit une variation de température ∆𝜃, sa variation d’énergie interne est donnée par la relation Δ𝑈 = 𝐶 𝛥𝜃 (𝐶 étant sa capacité thermique).
  • Rappel mathématique :

        \[\lim_{x \to +\infty}e^{-x}=0\]

Modélisation théorique

Le système étudié est la lunette astronomique. Il est en contact avec l’air extérieur qui joue le rôle de thermostat.

On considère qu’à chaque instant de date 𝑡 les différents constituants de la lunette sont à la même température 𝜃(𝑡).

La modélisation utilisée s’appuie sur la loi de Newton (Cf. encadré ci-dessus).

11. Indiquer le sens du transfert thermique qui a lieu au cours du refroidissement de la lunette.

12. Enoncer le premier principe de la thermodynamique.

13. Montrer que la variation de la température Δ𝜃 de la lunette sur une petite durée ∆𝑡 vérifie la relation :

𝐶 Δ𝜃 = ℎ 𝑆 (𝜃𝑒 − 𝜃)Δ𝑡                 (1)

C étant la capacité thermique de la lunette.

14. En déduire que la température 𝜃(𝑡) de la lunette vérifie l’équation différentielle :

\frac{d \theta (t)}{dt}+\frac{ \theta (t)}{\tau }=\frac{ \theta_e}{\tau }               (2)

où τ est le temps caractéristique du refroidissement, dont on précisera l’expression.

La solution de l’équation différentielle (2) est de la forme :

\theta (t)=Ae^{- \frac{t}{\tau}}+B  avec 𝐴 et 𝐵 deux constantes

15. Indiquer la valeur que devrait avoir la température de la lunette à l’issue du refroidissement. En déduire la valeur de la constante 𝐵.

16. Déterminer la valeur de la constante 𝐴, en fonction de 𝜃0 et 𝜃𝑒, en raisonnant sur la valeur de la température initiale de la lunette.

Simulation

La solution de l’équation différentielle a été utilisée pour réaliser un tracé sur la base des points expérimentaux, en laissant comme paramètre libre τ.

Les valeurs de 𝐴 et 𝐵 ont été fixées respectivement à 10,5 °C et 9,0 °C.

Le résultat est optimisé pour une valeur de τ = 1414 s (Voir graphique ci-contre).

Sur le graphique ci-contre, les points expérimentaux sont représentés par des ‘+’ et le modèle théorique optimisé est représenté par la courbe en trait plein.

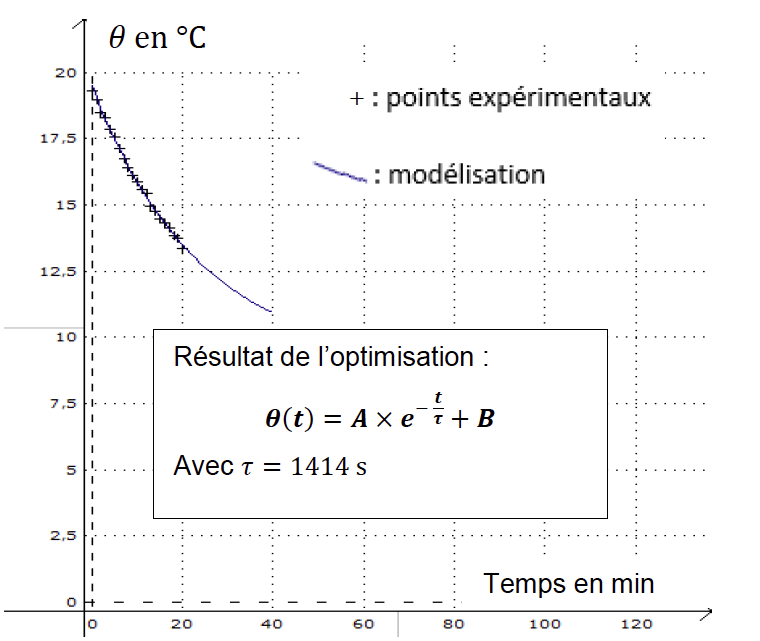
17. Discuter qualitativement l’accord du modèle théorique avec les résultats expérimentaux.

18. En utilisant le résultat de l’optimisation, vérifier que la lunette peut être considérée comme « à température » à la date t = 2,0 h

ANNEXE page 15/15 à rendre avec la copie