Métropole Septembre 2022 Sujet 2
Exercice 1– (10 points) – Commun à tous les candidats – Durée 1h45 – Calculatrice autorisée
Sujet n° 22-PYCJ2ME3
Sujet et corrigé
La plongée est une activité sportive qui nécessite de prendre des précautions importantes pour prévenir de nombreux risques (noyade, hypothermie…). Elle se pratique à l’aide de bouteilles d’air comprimé que le plongeur porte sur son dos tout au long de sa plongée.
L’objectif de cet exercice est d’étudier les conditions pour effectuer une plongée à une profondeur de 35 m.
1. Équilibre dynamique du plongeur
Dans le référentiel terrestre supposé galiléen, on considère le système {plongeur + équipement} de centre de masse G ; il est en équilibre à une profondeur de 35 m.
Donnée :
- la poussée d’Archimède est la force exercée par un fluide sur un système immergé dans ce fluide. Pour un système immergé entièrement, ses caractéristiques sont :
- direction : verticale ;
- sens : vers le haut ;
- norme : PA= ρ · V · g où ρ est la masse volumique du fluide, V est le volume du système immergé et g est l’intensité de pesanteur.
Q1. Identifier les deux forces modélisant les actions mécaniques exercées sur le système {plongeur + équipement} en équilibre.
Les deux forces modélisant les actions mécaniques exercées sur le système plongeur + équipement en équilibre sont :
Le poids $\vec{P}$
La poussée d’Archimède ${\vec{P}}_A$
Q2. À l’aide de la deuxième loi de Newton, représenter, sans souci d’échelle, les forces exercées sur le système sachant qu’il est en équilibre.
Système plongeur + équipement
Référentiel : Terrestre supposé galiléen
D’après la seconde loi de Newton :
$\Sigma{\vec{F}}_{ext}=m\vec{a}$
Or le système en équilibre : $\vec{a}=\vec{0}$
$\Sigma{\vec{F}}_{ext}=m\vec{0}$
$\Sigma{\vec{F}}_{ext}=\vec{0}$
$\vec{P}+{\vec{P}}_A=\vec{0}$
$\vec{P}=-{\vec{P}}_A$
$\vec{P}$ et ${\vec{P}}_A$ ont la même valeur, la même direction et un sens opposé.

Lorsque le plongeur inspire, le volume de ses poumons augmente.
Q3. Expliquer les conséquences de cette inspiration sur le mouvement du plongeur initialement immobile en justifiant, notamment, la direction et le sens du vecteur accélération.
Lors d’une inspiration, le volume augmente :
$P=m \times g$ le poids ne change pas
$P_A=\rho \times V \times g$ la poussée d’Archimède est proportionnelle au volume. Ainsi la poussée d’Archimède augmente.
$\Sigma{\vec{F}}_{ext}=m\vec{a}$
$\vec{P}+{\vec{P}}_A=m\vec{a}$
$\vec{a}$ est vertical dirigée le même sens que ${\vec{P}}_A$ donc vers le haut.
2. Durée de la plongée
Données :
- une pression de 1 bar est égale à 1×105 Pa ;
- conversion d’une température θ exprimée en degré Celsius en une température T exprimée en kelvin : T(K) = θ(°C) + 273 ;
- température de l’eau de mer supposée constante : Teau = 283 K ;
- pression initiale de l’air comprimé, modélisé par un gaz parfait, dans une bouteille de plongée : Pb = 230 bar ;
- constante des gaz parfaits : R = 8,31 J·mol–1·K–1 ;
- volume d’air total contenu dans les bouteilles de plongée : Vb = 30 L.
Une simulation de l’évolution de la pression dans l’eau de mer en fonction de la profondeur est représentée sur la figure 1.
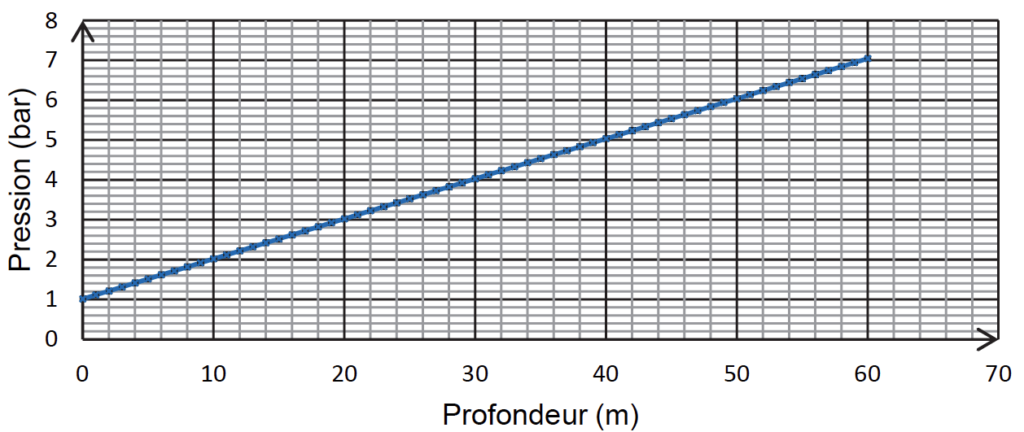
Figure 1. Simulation de l’évolution de la pression de l’eau en bar en fonction de la profondeur en mètre
Q4. Montrer que la quantité de matière initiale d’air comprimé contenue dans les bouteilles de plongée à la pression de 230 bar et à la température de 283 K vaut n = 293 mol.
D’après la loi des gaz parfaits :
$PV=nRT$
$nRT=PV$
$n=\dfrac{PV}{RT}$
$n=\dfrac{230 \times 1 \times {10}^5 \times 30 \times {10}^{-3}}{8,31 \times 283}$
$n=293\ \text{mol}$
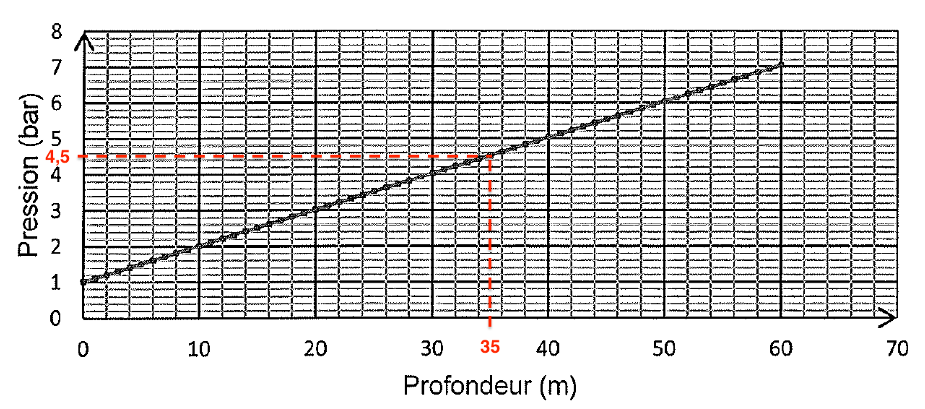
Q5. Déterminer graphiquement la valeur de la pression de l’eau à une profondeur de 35 m.
Graphiquement, à 35m de profondeur la pression $P$ à pour valeur $P=4{,}5\ \text{bar}$
Un détendeur permet de diminuer la pression de l’air en sortie des bouteilles. Ainsi, la pression de l’air respiré par le plongeur est égale à la pression de l’eau à la profondeur à laquelle il évolue. Dans ces conditions le plongeur consomme pour sa respiration 20,0 L d’air par minute.
Le plongeur prévoit d’utiliser la moitié de l’air à sa disposition pour son exploration à 35 m et l’autre moitié pour la descente et la remontée.
Q6. Estimer la valeur de la durée pendant laquelle le plongeur pourra effectuer son exploration à une profondeur de 35 m.
Calculons le volume disponible à cette pression :
$PV=nRT$
$V=\dfrac{nRT}{P}$
$V=\dfrac{293 \times 8{,}31 \times 283}{4{,}5 \times 1 \times {10}^5}$
$V=1{,}5\ \text{m}^3$
$V=1{,}5 \times {10}^3\ \text{L}$
Le plongeur prévoit d’utiliser la moitié de l’air soit un
$V_{utilisé}=\frac{V}{2}$
$V_{utilisé}=\dfrac{1{,}5 \times 10^3}{2}$
$V_{utilisé}=7{,}5 \times 10^2\ \text{L}$
Dans ces conditions le plongeur consomme $20{,}0\ \text{L}$ d’air par minute :
| 20,0 L | 1 min |
| $7{,}5 \times 10^2\ \text{L} $ | t |
$t=\dfrac{7{,}5 \times 10^2 \times 1}{20{,}0}$
$t=37{,}5\ \text{min}$
A une profondeur de 35m, le plongeur pourra effectuer son exploration pendant 37,5 min.
3. Intérêt de la combinaison
Dans cette partie on étudie l’évolution au cours du temps de la température T(t) du plongeur. La température du système {plongeur} est supposée homogène.
Données :
- masse du plongeur mp = 80 kg ;
- la température du plongeur avant la plongée est de 37 °C ;
- capacité thermique massique moyenne du corps humain : ch = 3,5×103 J·kg–1·K–1 ;
- puissance fournie au plongeur par son métabolisme pour maintenir sa température au cours de la plongée : Pm = 200 W ;
- résistance thermique totale modélisant le transfert thermique entre l’intérieur du corps humain et l’eau en prenant en compte le transfert thermique à travers les couches extérieures de la peau et la combinaison et le transfert entre la combinaison et l’eau : Req = 5,0×10–2 K· W–1 ;
- température de l’eau de mer supposée constante : Teau = 283 K ;
- on considère qu’un homme est en hypothermie légère lorsque la valeur de la température intérieure de son corps est inférieure à 35 °C.
On montre que l’expression du transfert thermique Q reçu par le plongeur entre les instants t et t + Δt s’écrit à l’aide de deux termes ① et ② :
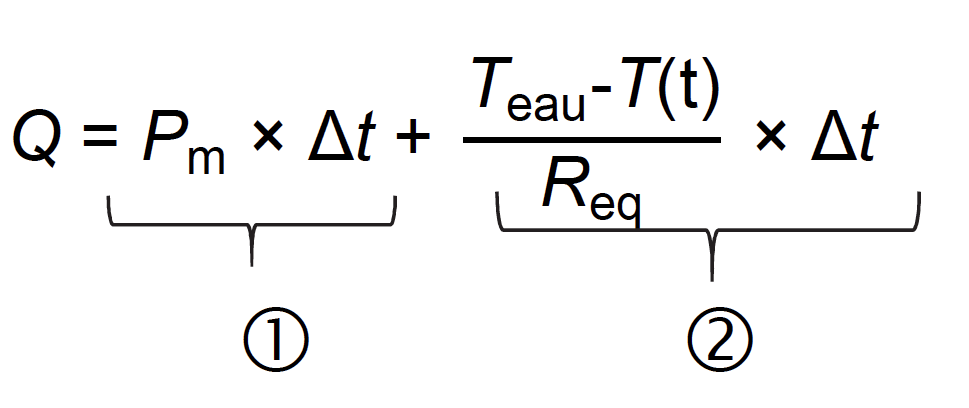
On suppose que Δt est faible devant la durée caractéristique d’évolution de la température T(t).
Q7. Indiquer quels phénomènes correspondent aux transferts thermiques associés respectivement aux termes ① et ②.
$1!:\ \ P_m \times \Delta t$ correspond à l’énergie fournie au plongeur par son métabolisme
$2!:\ \ \dfrac{T_{eau}-T(t)}{R_{eq}} \times \Delta t$ correspond au transfert thermique entre le plongeur et l’eau
Q8. Pendant cette durée Δt, la température du plongeur varie de ΔT. Exprimer la variation d’énergie interne ΔU du plongeur en fonction de mp, ch et ΔT.
$\Delta U=m_p \times c_h \times \Delta T$
Q9. À l’aide du premier principe de la thermodynamique, déduire que l’équation différentielle régissant l’évolution de la température T(t) du plongeur peut s’écrire sous la forme :
$\tau \frac{dT(t)}{dt}+T(t)=T_f $
avec τ= mp ∙ ch ∙ Req et Tf = Pm · Req + Teau
Premier principe de la thermodynamique :
$\Delta U=Q+W$
Ici $W=0$
$\Delta U=Q$
$\dfrac{\Delta U}{\Delta t}=\dfrac{Q}{\Delta t}$
Or
$\Delta U=m_p \times c_h \times \Delta T$
$Q=P_m \times \Delta t + \dfrac{T_{eau}-T(t)}{R_{eq}} \times \Delta t$
$m_p \times c_h \times \dfrac{\Delta T}{\Delta t}=P_m + \dfrac{T_{eau}-T(t)}{R_{eq}}$
$R_{eq} \times \left(m_p \times c_h \times \dfrac{\Delta T}{\Delta t}\right)=R_{eq} \times \left(P_m + \dfrac{T_{eau}-T(t)}{R_{eq}}\right)$
$R_{eq} \times m_p \times c_h \times \dfrac{\Delta T}{\Delta t}=R_{eq} \times P_m + T_{eau}-T(t)$
D’après l’énoncé : $\tau=R_{eq} \times m_p \times c_h$ et $T_f=P_m \times R_{eq}+T_{eau}$
Donc : $R_{eq} \times m_p \times c_h \times \dfrac{dT}{dt}=P_m \times R_{eq}+T_{eau}-T(t)$
$\tau \times \dfrac{dT}{dt}=T_f-T(t)$
On obtient une équation différentielle de la forme :
$\tau \times \dfrac{dT}{dt}+T(t)=T_f$
Q10. Préciser la signification physique du terme Tf.
$T_f$ est la température finale : la température d’équilibre du corps du plongeur.
La résolution de cette équation différentielle a permis d’obtenir, dans le cadre de ce modèle, la représentation temporelle de la température T en fonction du temps pour un plongeur avec combinaison en néoprène puis pour un plongeur sans combinaison (cf. figure 2).
Q11. Parmi les deux représentations de la figure 2, choisir, en justifiant la réponse, celle qui correspond à l’évolution de la température du plongeur avec sa combinaison et sans sa combinaison. Vérifier la cohérence de votre choix avec les expressions des grandeurs Tf et τ données dans la question 9.
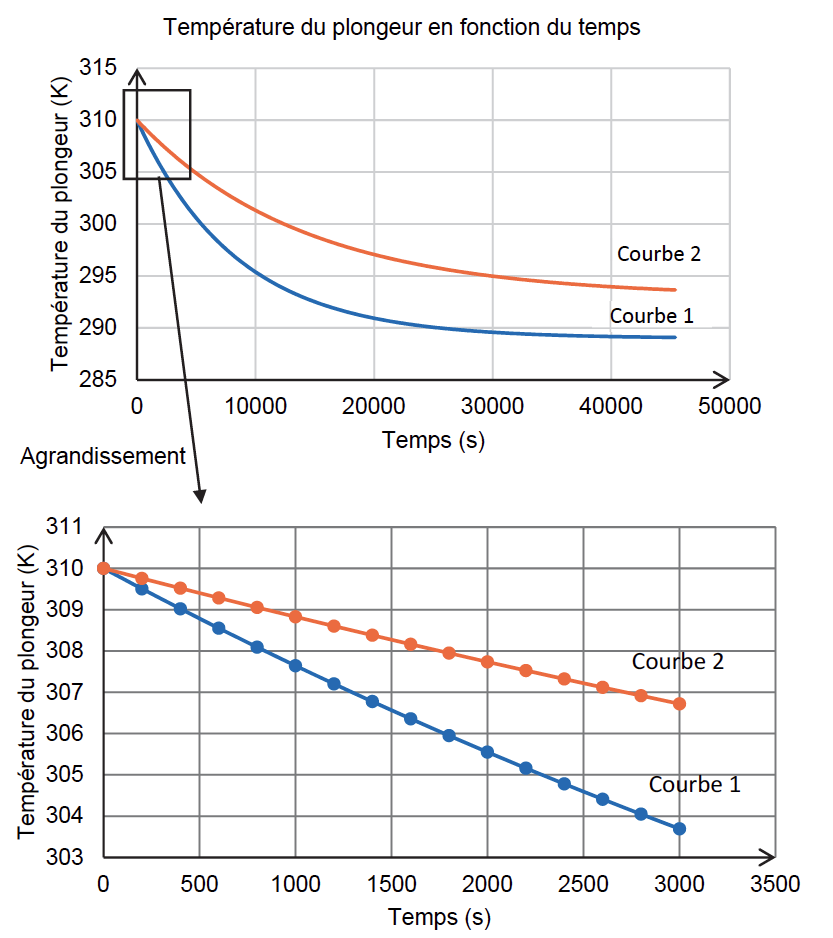
Figure 2. Modélisation de l’évolution de la température du plongeur avec et sans combinaison Le plongeur prévoit une sortie d’une durée totale de 60 minutes.
Lorsque le plongeur porte une combinaison, son corps refroidit moins rapidement.
Ainsi :
La courbe 2 correspond à l’évolution de la température avec combinaison
La courbe 1 correspond à l’évolution de la température sans combinaison
Calculons $\tau$ et $T_f$ :
$\tau=R_{eq} \times m_p \times c_h$
$\tau=5{,}0{.}10^{-2} \times 80 \times 3{,}5{.}10^3$
$\tau=1{,}4{.}10^4\ \text{s}$
$T_f=P_m \times R_{eq}+T_{eau}$
$T_f=200 \times 5{,}0{.}10^{-2}+283$
$T_f=293\ \text{K}$
Graphiquement $T_f=293\ \text{K}$ pour la courbe 2.
Le choix 2 est donc cohérent avec la valeur de $T_f$.
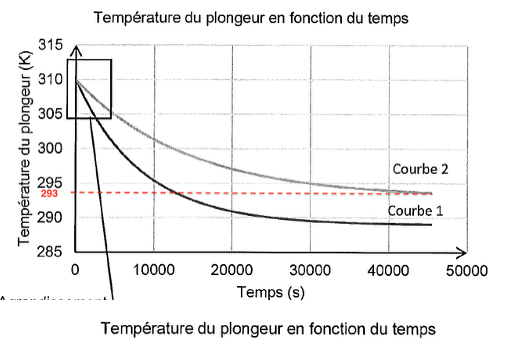
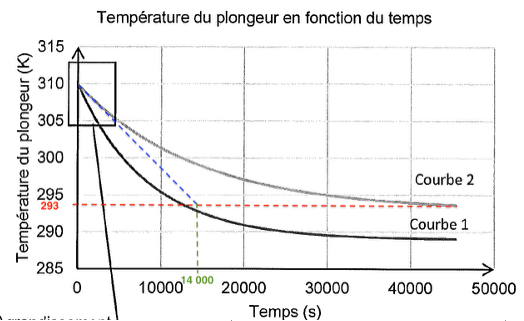
Graphiquement $\tau=14000=1{,}4{.}10^4\ \text{s}$ pour la courbe 2.
Le choix 2 est donc cohérent avec la valeur de $\tau$.
Q12. Déterminer la durée au bout de laquelle le plongeur muni de sa combinaison risquerait, dans le cadre de ce modèle, l’hypothermie. Commenter le résultat.
D’après les données, on considère qu’un homme est en hypothermie légère lorsque la valeur de la température intérieure de son corps est inferieure à $35^\circ\text{C}$.
$35^\circ\text{C}=35+273=308\ \text{K}$
Le plongeur est muni de sa combinaison : courbe 2.
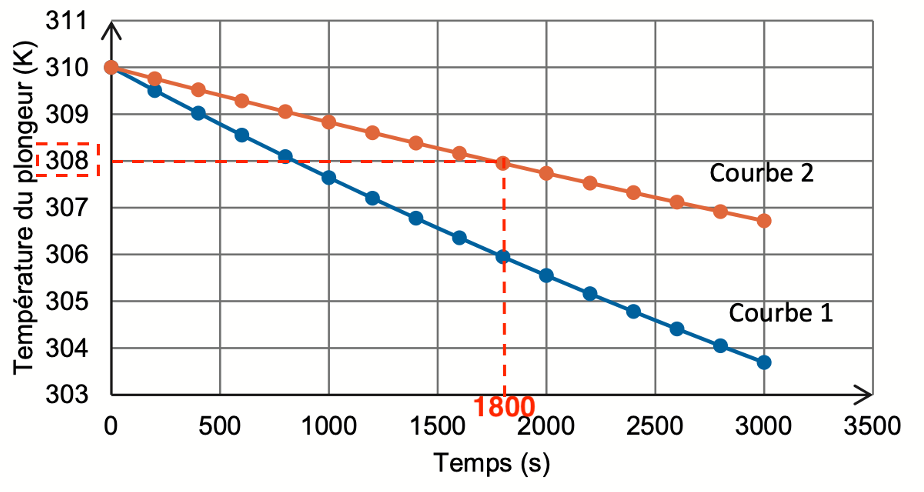
Graphiquement, la température intérieure de son corps est inferieure à $35^\circ\text{C}$ ($308\ \text{K}$) pour un temps supérieur à $1800\ \text{s}$ soit
$\dfrac{1800}{60}=30\ \text{min}$
Le plongeur prévoit une sortie d’une durée totale de 60 minutes.
Ce temps est donc insuffisant pour faire une plongée.
