Formule 1 : Freinage en ligne droite

Asie 2022 Sujet 1

Exercice A – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée

Sujet n° 22-PYCJ1JA1

Mots-clés: mécanique, lois de Newton, modélisation.

Les performances des voitures de Formule 1 sont aujourd’hui telles que certains circuits doivent être en partie redessinés pour éviter aux pilotes de prendre trop de risques. En effet, lors d’un freinage, le pilote peut subir des décélérations de plus de 6 G, sachant qu’une accélération de 1G correspond à l’accélération de la pesanteur soit à 9,81 m·s^-2 : c’est plus que ce que subit un spationaute au décollage d’une fusée !

L’objectif de cet exercice est d’étudier la prise de risque d’un.e pilote de Formule 1 pendant un freinage sur un circuit.

L’étude est effectuée lors de la décélération dans la ligne droite juste avant le virage n° 10 du circuit de Barcelone (voir la figure 1 ci-dessous).

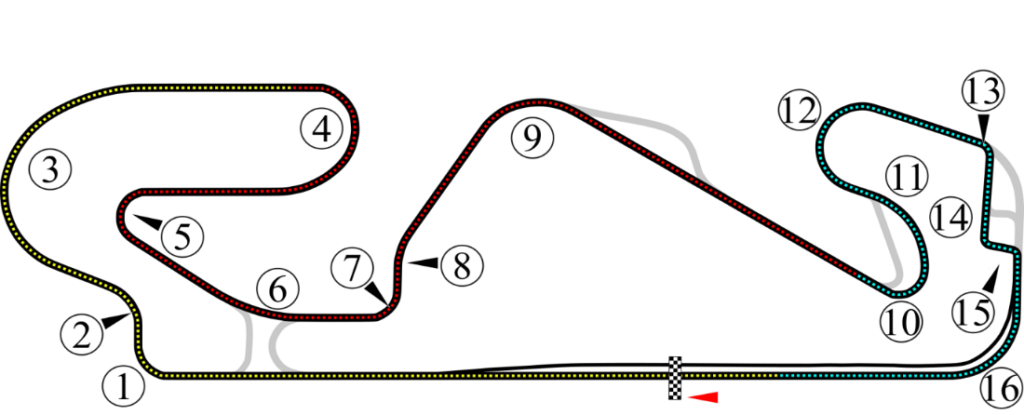
Fig. 1 – Circuit de Barcelone – Les virages sont indiqués par des numéros – D’après Wikipédia

On étudie le mouvement du centre de masse G du système {voiture + pilote}, de masse 𝑚, dans le référentiel terrestre considéré comme étant galiléen.

Utilisation d’un modèle simple

Le système {voiture + pilote} se déplace à l’horizontale, en ligne droite, à grande vitesse. Il freine du point A au point B (voir la figure 2 ci-contre) avant d’entrer dans le virage n° 10.

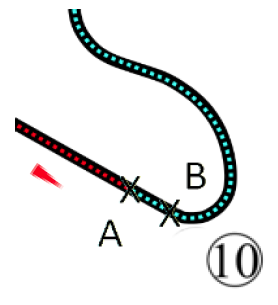
Pour simplifier l’étude, on modélise la situation de la manière suivante :

Lors du freinage le système {pilote + voiture} subit :
- son poids $\overrightarrow{P}$
- la résultante des forces exercées par la route sur les pneus que l’on peut décomposer en deux forces :

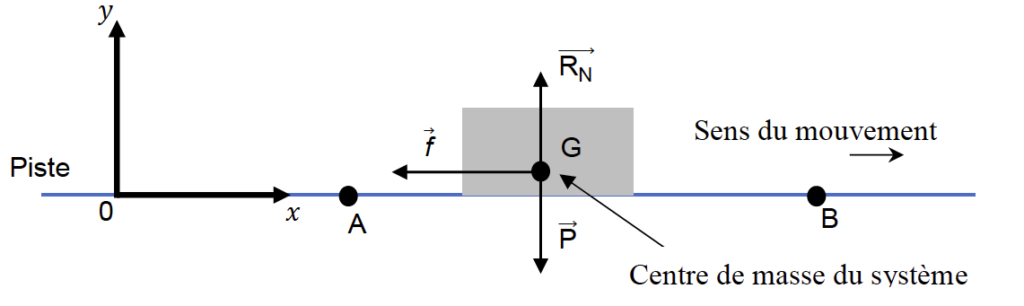
une force $\overrightarrow{R_N}$ verticale vers le haut (voir la figure 3) qui, dans le cas de ce mouvement, compense le poids $\overrightarrow{P}$ ;
une force $\overrightarrow{f}$ horizontale, de valeur 𝑓, de sens opposé au déplacement et modélisant l’ensemble des frottements subis par la voiture lors de son déplacement (voir la figure 3).
On fait l’hypothèse que la force $\overrightarrow{f}$ reste constante durant le freinage.
Le freinage commence à la date 𝑡 = 0 lorsque le centre de masse se trouve au point A. La vitesse a alors pour valeur 𝑣_𝐴 = 321 km·h^-1.

L’étude est réalisée dans le repère (𝑂𝑥𝑦), l’axe (𝑂𝑥) étant horizontal et orienté dans le sens du mouvement (voir la figure 3). Le mouvement a lieu le long de l’axe (𝑂𝑥).

1. En appliquant la deuxième loi de Newton, montrer que les coordonnées du vecteur accélération du système $\overrightarrow{a}$ sont :

$\overrightarrow{a}= \begin{cases} a_x(t)=-\frac{f}{m} \\ a_y(t)=0 \end{cases}$

Système { voiture + pilote }

Référentiel terrestre supposé galiléen

D’après la deuxième loi de newton :

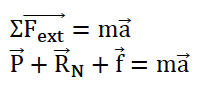
D’après le texte : une force $\overrightarrow{R_N}$ verticale vers le haut (voir la figure 3) qui, dans le cas de ce mouvement, compense le poids $\overrightarrow{P}$ ;

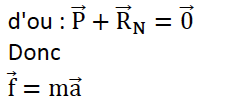
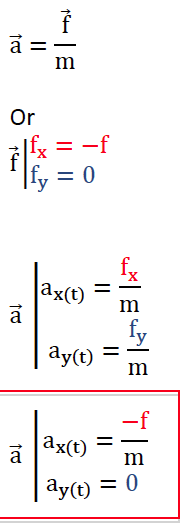
On désigne par Δ𝑣 = 𝑣_𝐵 − 𝑣_𝐴 la variation de la vitesse entre les points A et B et par ∆t la durée du mouvement entre A et B.

2. Justifier que, dans le cadre de cette étude, on peut écrire Δ𝑣 = 𝑎_𝑥 ∆t.

Réponse :

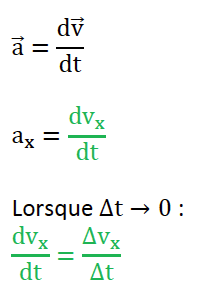
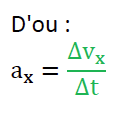
Or le mouvement est horizontal :

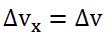
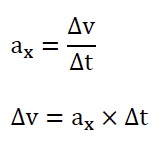
La vitesse passe de la valeur 𝑣_𝐴 = 321 km·h^-1 au point A à la valeur 𝑣_𝐵 = 84 km·h^-1 au point B pendant la durée ∆t = 1,50 s.

3. Calculer la valeur de l’accélération (en m ⋅ s⁻²) à partir de ces données. La comparer avec la valeur de 6 G mentionnée dans le texte introductif. On rappelle : 1 G = 9,81 m ⋅ s⁻².

Réponse :

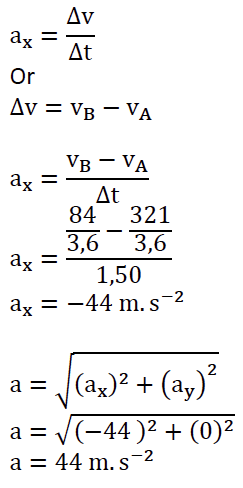
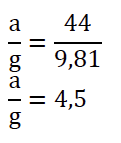
la valeur de l’accélération est de 4,5G.

D’après le texte : « lors d’un freinage, le pilote peut subir des décélérations de plus de 6G ».

Dans notre cas la décélération est moins importante.

La figure 4 indique les limites de tolérance d’un individu en prenant en compte la valeur de l’accélération (en G) et la durée durant laquelle il la subit. Dans la zone de danger des perturbations physiologiques touchant les appareils cardiovasculaire et pulmonaire peuvent apparaître.

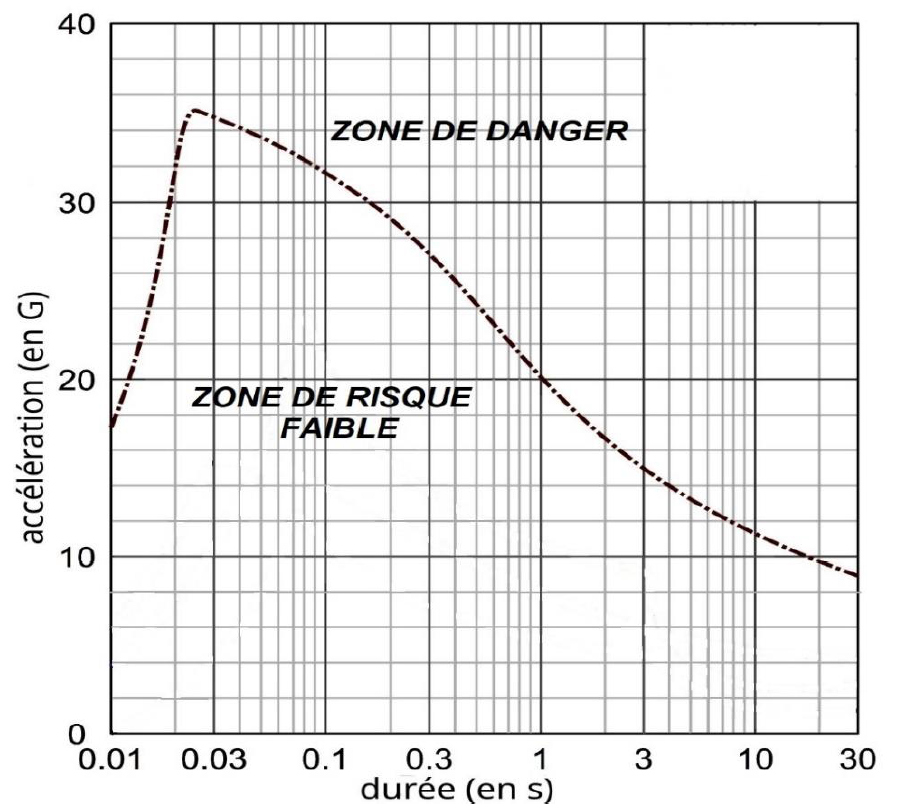
***Fig.4 –*** *Limites de tolérance d’un individu à l’accélération*

4. Indiquer si le pilote prend un risque pour sa santé lors du freinage.

Réponse :

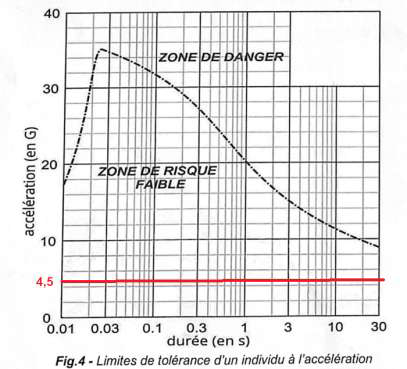
Quelque soit le temps que dure le freinage, le risque pour la santé est faible.

Validité du modèle simplifié

Pour tester la validité du modèle précédent, on compare l’évolution de la vitesse en fonction du temps prévue par le modèle à celle déduite des mesures réalisées grâce aux capteurs embarqués.

5. Montrer que, dans le cadre du modèle simplifié utilisé, la coordonnée 𝑣𝑥(𝑡) du vecteur vitesse a pour expression en fonction du temps lors du freinage :

$v_x(t)=-\frac{f}{m}t+v_A$ avec 𝑣_𝐴 = 89 m · s⁻¹

Réponse :

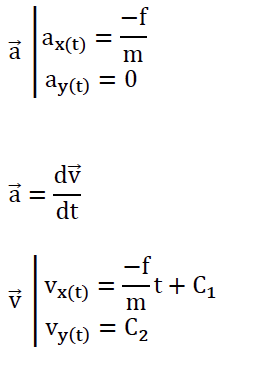
Les relevés effectués lors de l’intégralité du freinage du virage 10 permettent d’obtenir la coordonnée 𝑣𝑥 du vecteur vitesse en temps réel et de tracer le graphique présenté sur la figure 5.

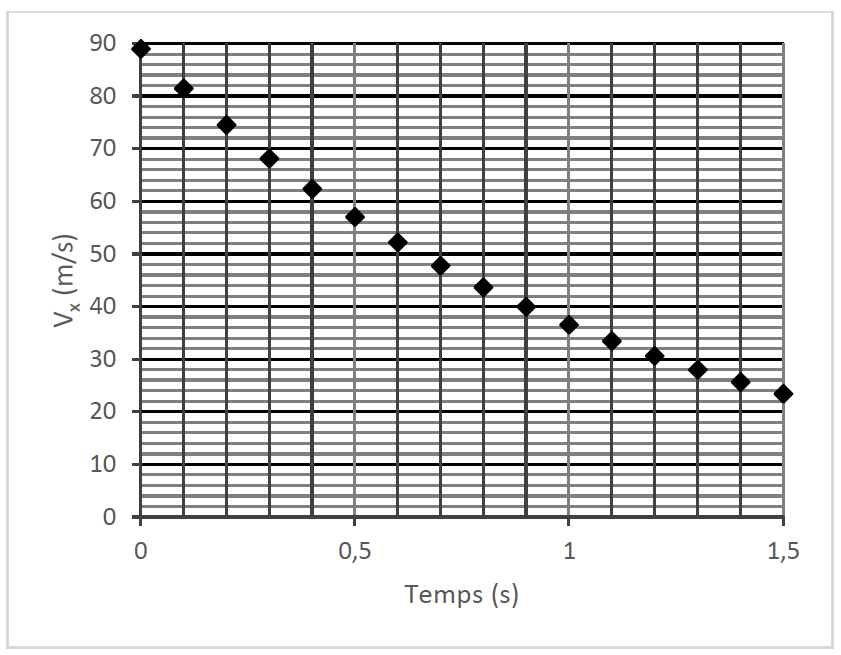
***Fig.5 –*** *Relevé de la coordonnée suivant* 𝑥 *de la vitesse lors du freinage.*

6. Comparer l’allure du graphique de la figure 5 avec l’allure prédite par la modélisation à la question précédente.

Réponse :

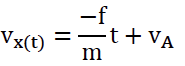
La modélisation est une fonction affine : une droite ne passant pas par l’origine.

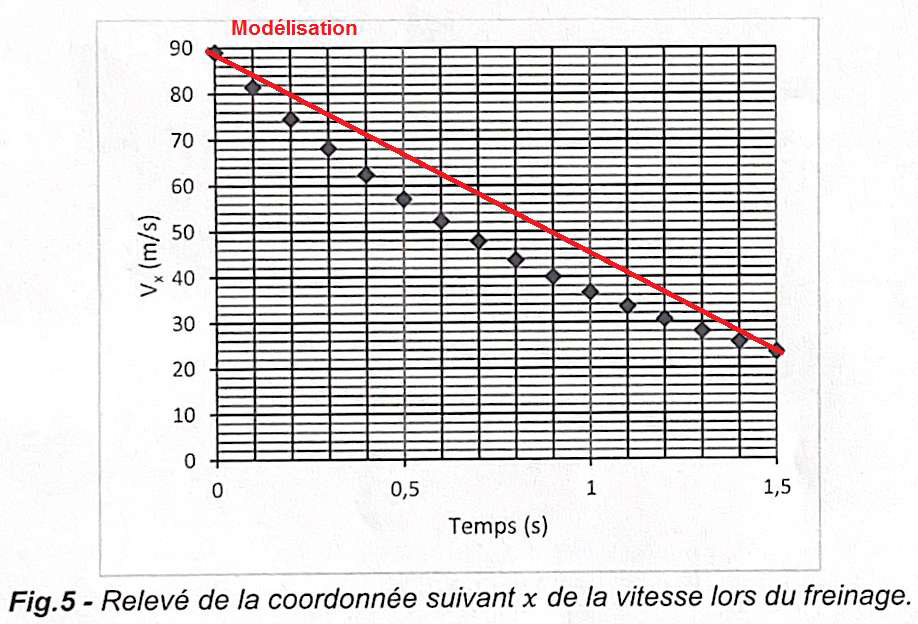
L’allure de la courbe de la vitesse expérimentale ne correspond pas à l’allure de la modélisation à la question précédente.

7. Indiquer quelle hypothèse de la modélisation précédente doit être remise en question si on considère l’intégralité du freinage.

Nous avons fait l’hypothèse que la force f reste constante durant le freinage.

Cette hypothèse doit être remise en question car l’allure de la courbe de la vitesse expérimentale ne correspond pas à l’allure de la modélisation.