Bac Asie 2021 Sujet 2
Exercice A – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n° 21-PYCJ2JA1
Sujet et corrigé
Mots-clés : premier principe et loi phénoménologique de Newton, intensité sonore, atténuation.
Déguster un vin à la bonne température est essentiel pour pouvoir en apprécier les saveurs gustatives et odorantes : un vin trop tiède n’est pas agréable ; un vin trop froid voit ses arômes masqués par l’alcool. Pour pouvoir servir les vins à la bonne température, on utilise des caves à vin.

Cave à vin
Photo Wikipédia
On s’intéresse à une bouteille de vin rouge léger dont la température idéale de service est de 13° C. Initialement, cette bouteille et son contenu sont à une température voisine de 22° C. On place cette bouteille dans la cave à vin afin d’optimiser sa dégustation.
L’air à l’intérieur de la cave à vin joue le rôle d’un thermostat. Sa température Tair demeure constante et égale à 13 °C.
Dans cet exercice, on cherche à déterminer la durée nécessaire pour que la température du vin atteigne la valeur souhaitée de 13 °C (partie 1). On étudie ensuite la gêne sonore pouvant être occasionnée par une cave à vin dans un restaurant (partie 2).
Les deux parties sont indépendantes.
Partie 1 – Evolution de la température – Durée du refroidissement
On s’intéresse à l’évolution de la température T du système {vin + bouteille} placé dans le thermostat. Le système {vin + bouteille} est immobile. L’air de la cave à vin est ventilé.
On désigne par 𝑄 le transfert thermique entre l’air et le système, et par Φ le flux thermique correspondant, c’est-à-dire le transfert thermique par unité de temps.
Le transfert thermique et le flux thermique sont comptés positivement si le transfert thermique a lieu de l’air vers le système.
On fait l’hypothèse que le flux thermique Φ vérifie la loi phénoménologique de Newton.
Loi phénoménologique de Newton
Lorsqu’un système incompressible de température T est placé dans un fluide en écoulement à la température Ta , il s’établit un flux thermique entre le thermostat et le système proportionnel à l’écart de température (T − Ta).
On peut alors écrire : Φ = −ℎ × S × (T − Ta)
- S est la surface d’échange entre le système et le thermostat (en m2) ;
- ℎ est le coefficient d’échange convectif (en W ⋅ m−2 ⋅ K−1).
Données
- Surface d’échange entre la bouteille et l’air : S = 4,66 × 10−2 m2
- Coefficient d’échange convectif : ℎ = 10 W ⋅ m−2 ⋅ K−1
- Capacité thermique du système {vin + bouteille} : C = 3,25 kJ ⋅ K−1
- T(K) = 𝜃(°C) + 273
1. À l’aide du premier principe de la thermodynamique, relier la variation d’énergie interne ΔU du système {vin + bouteille} au transfert thermique 𝑄 entre l’air et le système.
∆U=Q+W
Or W=0
Donc ∆U=Q
2. Exprimer le transfert thermique 𝑄 pendant une durée très petite Δ𝑡 en fonction du flux thermique 𝛷 supposé constant pendant cette durée et de Δ𝑡. Rappeler les unités, dans le système international, des grandeurs intervenant dans cette expression.
$$\Phi=\frac{Q}{\Delta t }$$
$$Q=\Phi \times \Delta t$$
Avec :
- en Joule (J)
- en Watt (W)
- en seconde (s)
La variation d’énergie interne d’un système incompressible au repos dont la température varie de ∆U est donnée par la relation 𝛥U = C × ΔT (C est la capacité thermique du système).
3. Exprimer le flux thermique Φ en fonction de la capacité thermique C du système supposé incompressible, de sa variation de température ΔT et de la durée Δ𝑡.
$$\Phi=\frac{Q}{\Delta t }$$
Or $$Q=\Delta U=C \times \Delta T$$
Donc
$$\Phi=\frac{C \times \Delta T}{\Delta t } $$
4. En utilisant la loi phénoménologique de Newton, et en faisant tendre Δ𝑡 vers 0, vérifier que l’équation différentielle qui régit l’évolution de la température T s’écrit :
$\frac{dT}{dt} =- \frac{1}{\tau}(T-T_{air}) $
En déduire l’expression et l’unité de 𝜏.
$$\phi=-h \times S \times \left(T-T_a\right)$$
$$C \times \frac{\Delta T}{\Delta t} =-h \times S \times (T-Ta)$$
en faisant tendre Δt vers 0
$$\frac{\Delta T}{\Delta t}=\frac{dT}{dt}$$
$$C \times \frac{dT}{dt}=-h \times S \times \left(T-T_a\right)$$
$$\frac{dT}{dt}=-\frac{h \times S}{C} \times \left(T-T_a\right)$$
L’équation différentielle qui régit l’évolution de la température T s’écrit :
$$\frac{dT}{dt}=-\frac{1}{\tau} \times \left(T-T_a\right)$$
Avec
$$\frac{1}{\tau}=\frac{h \times S}{C}$$
$$\tau=\frac{C}{h \times S}$$
Unité de $\tau$ :
$$\left[\tau\right]=\frac{\left[C\right]}{\left[h\right] \times \left[S\right]}$$
$$\left[\tau\right]=\frac{J.K^{-1}}{W.m^{-2}K^{-1} \times m^2}$$
$$\left[\tau\right]=\frac{J}{W}$$
Or $Q=\Phi \times \Delta t$
donc J=W.s
donc
$$\left[\tau\right]=\frac{W.s}{W}$$
$$\left[\tau\right]=s$$
L’unité de $\tau$ est la seconde.
Le modèle d’évolution temporelle de la température du système {vin + bouteille}, solution de l’équation différentielle, est le suivant :
$T(t) =(T_0-T_{air}) e^{-\frac{t}{\tau}} +T_{air}$
Cette évolution temporelle de la température T(𝑡) est représentée ci-dessous :
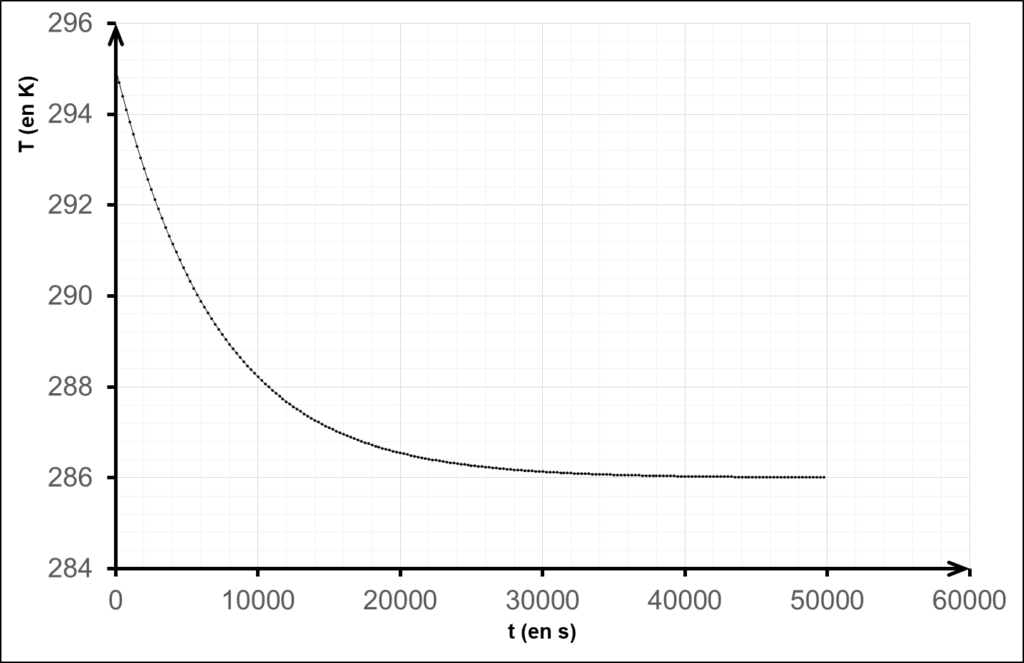
5. Retrouver à l’aide des résultats de la modélisation les valeurs de T0 et de Tair.
$$T(t)=(T_0-T_{air}){ \times e}^{-\frac{t}{\tau}}+T_{air}$$
A t=0 :
$$T_{(t=0)}=(T_0-T_{air}){ \times e}^{-\frac{0}{\tau}}+T_{air}$$
$$T_{(t=0)}=T_0-T_{air}+T_{air}$$
$$T_{(t=0)}=T_0$$
Graphiquement
$$T_{(t=0)}=295°K$$
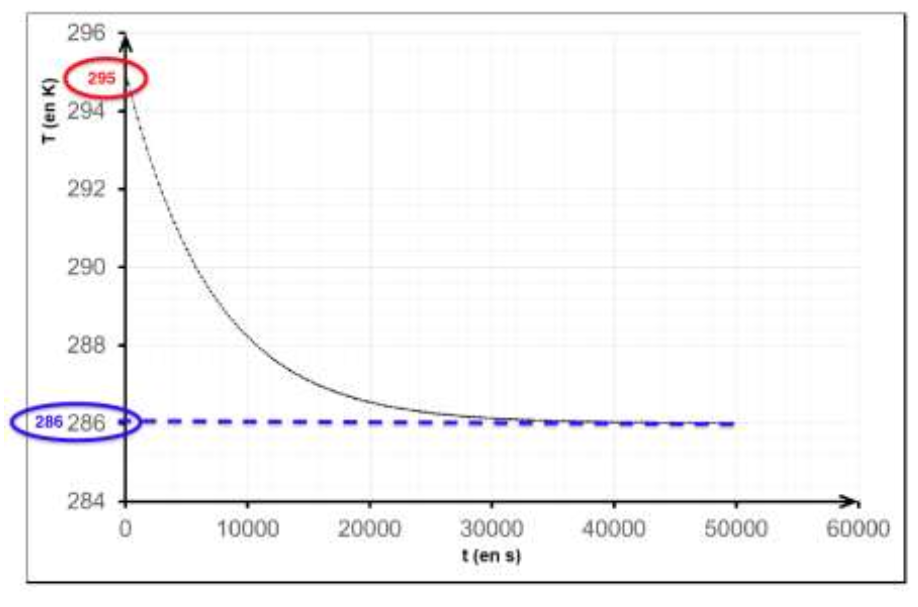
D’ou $T_0=295°K$
A $t\rightarrow\infty$
$$T_{(t\rightarrow\infty)}=(T_0-T_{air}){ \times e}^{-\frac{\infty}{\tau}}+T_{air}$$
$$T_{(t\rightarrow\infty)}=T_{air}$$
Graphiquement
$$T_{(t\rightarrow\infty)}=286\ °K$$
D’ou $T_{air}=286\ °K$
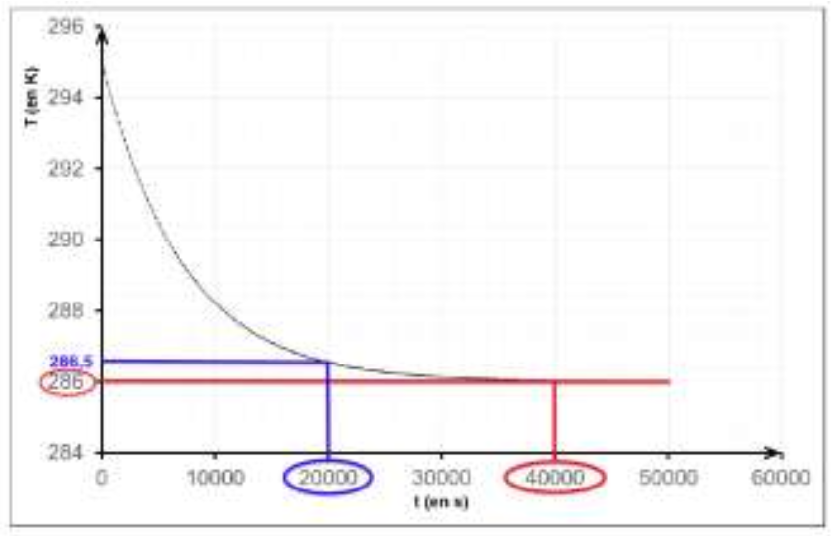
6. Estimer graphiquement au bout de combien de temps le vin pourra être servi à la température souhaitée (à 0,5 degré près).
« On s’intéresse à une bouteille de vin rouge léger dont la température idéale de service est de 13° C. »
Le vin pourra être servi à la température souhaitée (à 0,5 degré près) soit à partir de 13,5°C.
13,5°C=13,5+273=286,5°K
Le vin atteint la température de 286,5°K pour une durée de 20 000 s soit environs 5h30.
Remarque : pour atteindre 13° il aurait fallu attendre
40 000 s soit le double du temps pour un gain de 0,5°.
Partie 2 – Cave à vin et niveau d’intensité sonore
Le niveau d’intensité sonore moyen d’une cave à vin est de 42 dB à environ 1,0 m avec une fréquence sonore voisine de 200 Hz. Un restaurateur a besoin de deux caves à vin dans un même local fermé, à proximité de la salle qui accueille les clients. Il cherche à savoir si des clients assis juste derrière la cloison, à 1,0 m des
caves à vin, sont susceptibles de les entendre.
Données
- Niveau d’intensité sonore L en décibel :
$L=10 log \left (\frac{I}{I_0}\right) $ avec I0 = 1,0 × 10-12 W·m-2.
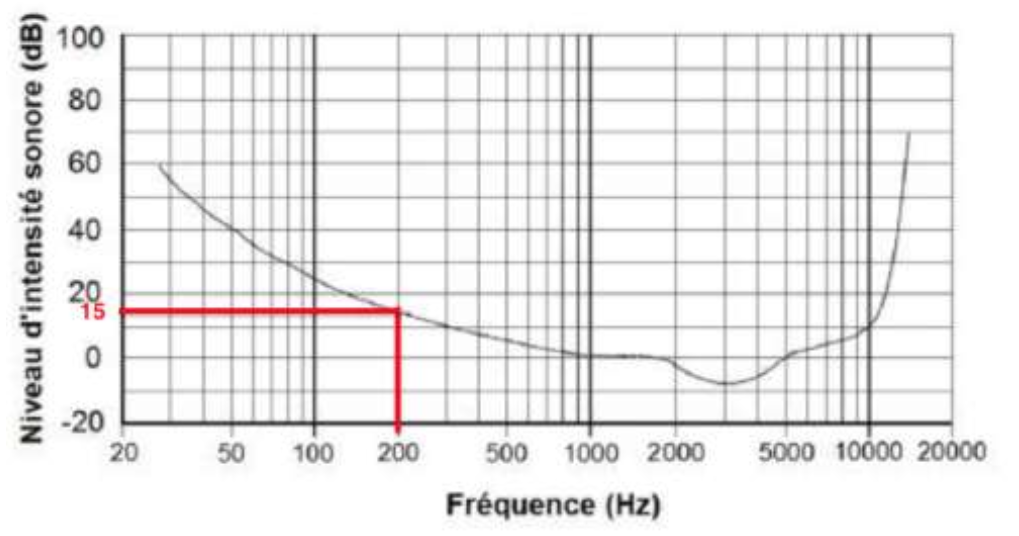
- Seuil d’audibilité en fonction de la fréquence : le graphique suivant indique les valeurs minimales de niveau d’intensité sonore audible en fonction de la fréquence.
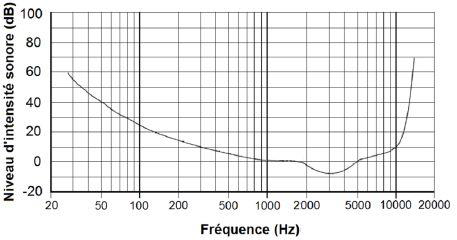
- Atténuation par absorption : l’atténuation par absorption pour les bruits aériens, notée A, correspond à la différence entre le niveau d’intensité sonore L𝑖 du son incident sur un obstacle et le niveau d’intensité sonore L𝑡 du son transmis. Elle varie avec la fréquence. Pour les cloisons du restaurant,
les caractéristiques d’atténuation sonore sont données ci-dessous :
| 𝒇 (en 𝐇z ) | 100 | 125 | 160 | 200 | 250 | 315 | 400 | 500 | 630 |
| 𝑨 (en d𝐁) | 29 | 32 | 28 | 25 | 29 | 33 | 36 | 38 | 41 |
7. Montrer que le niveau sonore total émis par les deux caves à vin, à 1,0 m de celle-ci sans la cloison serait de 45 dB.
$$L=10\log(\frac{I}{I_0}) $$
$$L_{Total}=10\log(\frac{I_{Total}}{I_0})$$
Or $I_{Total}=2I$
$$L_{Total}=10\log(\frac{2I}{I_0})$$
$$L_{Total}=10\log{\left(2\right)}+10\log(\frac{I}{I_0})$$
$$L_{Total}=3+L$$
$$L_{Total}=3+42=45dB$$
8. Le signal sonore émis par les deux caves serait-il audible par les clients placés derrière la cloison ? Justifier.
« Le niveau d’intensité sonore moyen d’une cave à vin est de 42 dB à environ 1,0 m avec une fréquence sonore voisine de 200 Hz. »
Pour une fréquence de 200 Hz , l’atténuation est de 25 dB.

Signal reçu par les clients : 45-25=20 dB
Le seuil d’audibilité pour une fréquence de 200 Hz est de 15dB.
Ainsi le signal sonore émis par les deux caves sera audible par les clients placés derrière la cloison.