Bac Métropole Mars 2021 Sujet 2
Exercice B – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet et corrigé
Mot-clé : modèle du circuit RC série
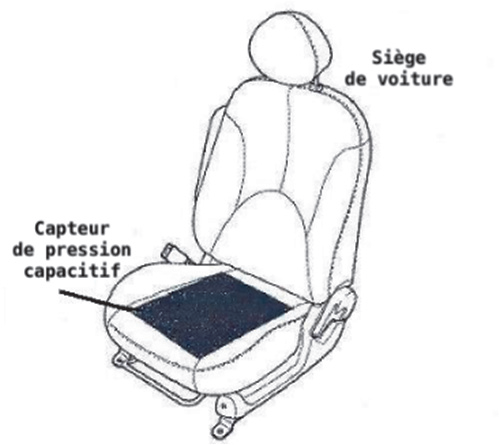
Pour renforcer la sécurité routière, les voitures sont équipées d’un système de détection de la présence d’un passager pour lui signaler si sa ceinture de sécurité est bien attachée.
Dans le cadre d’un projet scientifique, un groupe d’élèves réalise un système de détection semblable à celui d’une voiture. Il est composé d’un capteur de pression capacitif « artisanal » associé à un microcontrôleur.
Le condensateur « artisanal » est constitué de deux feuilles d’aluminium séparées par une feuille de papier isolante. Lorsqu’un objet de masse m est posé dessus, il exerce une pression sur les deux feuilles d’aluminium et les déforme, ce qui modifie la capacité électrique du condensateur « artisanal ». Après un traitement numérique des signaux électriques, le microcontrôleur peut détecter la présence de l’objet.

L’objectif de cet exercice est d’illustrer le principe de fonctionnement d’un tel capteur.
1. Étude du capteur de pression capacitif « artisanal »
Le capteur de pression capacitif « artisanal » est représenté en coupe à la figure 3.
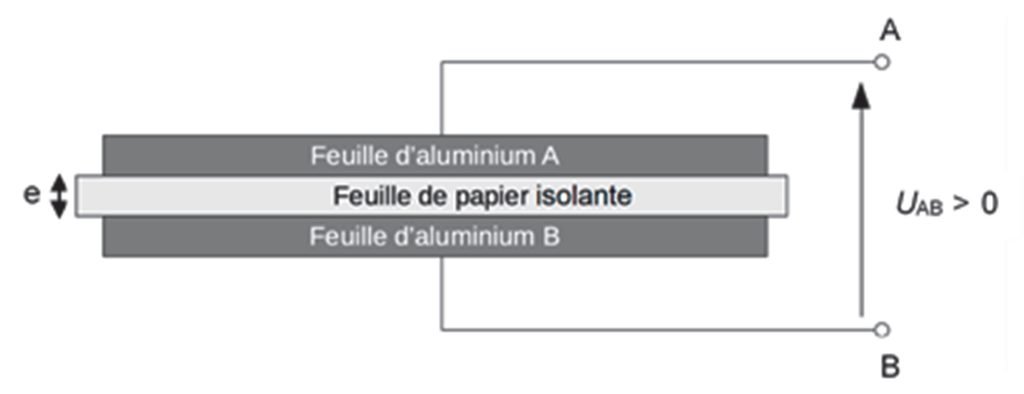
1.1. Justifier l’utilisation de l’adjectif « capacitif » dans l’expression « capteur de pression capacitif » couramment utilisée pour désigner ce genre de capteurs.
Des charges de signe opposé s’accumulent sur les plaques A et B. Ce phénomène est appelé effet capacitif.
Ici cet effet dépend de la pression exercée sur les plaques d’ou l’expression « capteur de pression capacitif »
1.2. Si le capteur est soumis à une tension positive constante UAB entre ses bornes A et B, des charges électriques apparaissent sur chacune des feuilles, notées QA sur la feuille d’aluminium A et QB sur la feuille d’aluminium B. On note C la capacité électrique de ce capteur. Donner l’expression littérale de la charge QA puis celle de la charge QB en fonction de C et UAB.
$$U_{AB}=V_A-V_B$$
$$U_{AB}>0$$
$$V_A-V_B>0$$
$$V_A>V_B$$
La plaque A constitue la plaque positive et la plaque B négative.
$$Q_A=C \times U_{AB}$$
$$Q_B=-Q_A=-C \times U_{AB}$$
1.3. La capacité électrique C d’un tel capteur s’écrit $C= \frac{ \epsilon \times S }{e}$ avec S la surface en regard des feuilles e d’aluminium, e l’épaisseur de la feuille de papier isolante et ε une constante caractéristique de la feuille de papier isolante. Indiquer, en justifiant la réponse, le sens de variation de la capacité électrique C du capteur quand un objet est posé sur le condensateur « artisanal ».
$$C=\frac{\varepsilon \times S}{e}$$
Quand un objet est posé sur le condensateur « artisanal » e diminue, ainsi C augmente car C et e sont inversement proportionnels.
2. Modélisation du circuit de la chaine de mesure
La détection de la variation de la capacité électrique C du capteur est réalisée par un circuit électrique appelé la chaîne de mesure. Le circuit électrique associé peut se modéliser par le circuit schématisé ci-après :
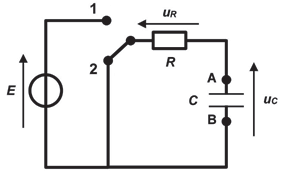
Le générateur de ce circuit est un générateur idéal de tension E. Le condensateur modélise le capteur de pression capacitif « artisanal » installé dans l’assise du siège du véhicule. La mesure de la tension aux bornes du condensateur, notée uC(t), est réalisée en permanence par un microcontrôleur qui n’est pas représenté sur le schéma. La résistance R est celle d’un conducteur ohmique. Le capteur de pression capacitif « artisanal » possède une capacité électrique C variable, selon que le capteur est soumis ou non à une pression extérieure. Le commutateur possède deux positions notées 1 et 2 et joue le rôle d’un interrupteur fermé sur la position 1 ou sur la position 2.
On considère que l’interrupteur est dans la position 1 depuis un temps très long, et que les paramètres E, C et R sont constants. À la date t = 0 s, uC(0) = E et l’interrupteur est basculé dans la position 2.
2.1. Établir l’équation différentielle régissant l’évolution de la tension uC(t) aux bornes du condensateur pour t ≥ 0 et l’écrire sous la forme :
$\frac{d u_C(t)}{dt}+\frac{u_C(t)}{\tau} =0 $ Exprimer τ en fonction de R et C.
Réponse :
« l’interrupteur est basculé dans la position 2 »
D’après la loi d’additivité des tensions ou loi des mailles :
$U_C(t)+U_R(t)=0$
Or $U_R(t)=R \times i$
$U_C(t)+R \times i=0$
Or $ i(t)=\frac{dq(t)}{dt}$
$U_C(t)+R \times \frac{dq(t)}{dt}=0$
Or $q(t)=C \times U_C(t)$
$U_C(t)+R \times \frac{C \times U_C(t)}{dt}=0$
$U_C(t)+RC \times \frac{U_C(t)}{dt}=0$
On divise par RC
\frac{1}{RC}U_C(t)+\frac{dU_C(t)}{dt}=0
$$\frac{dU_C(t)}{dt}+\frac{1}{RC}U_C(t)=0$$
On obtient une équation différentielle sous la forme :
$$\frac{dU_C(t)}{dt}+\frac{1}{\tau}U_C(t)=0$$
Par identification : $\tau=RC$
2.2. Vérifier que $u_C(t)=A e^{-\frac{t}{\tau}} $ est solution de l’équation différentielle et exprimer A en fonction de E.
Vérifions que les solutions de cette équation différentielle sont de la forme :
$$U_C\left(t\right)=Ae^{-\frac{t}{\tau}}$$
-Dérivons $U_C\left(t\right)$ :
$$\frac{dU_C(t)}{dt}=-\frac{A}{\tau}e^{-\frac{t}{\tau}}$$
-Remplaçons $U_C\left(t\right)$ et $\frac{dU_C(t)}{dt}$ dans l’équation :
$$\frac{dU_C(t)}{dt}+\frac{1}{\tau}U_C\left(t\right)=-\frac{A}{\tau}e^{-\frac{t}{\tau}}+\frac{1}{\tau}\left(Ae^{-\frac{t}{\tau}}\right)=-\frac{A}{\tau}e^{-\frac{t}{\tau}}+\frac{1}{\tau}Ae^{-\frac{t}{\tau}}=0$$
La solution de la forme $U_C\left(t\right)=Ae^{-\frac{t}{\tau}} $ vérifie l’équation différentielle.
Exprimons A en fonction de E.
$$U_C\left(t=0\right)=E$$
$$Ae^{-\frac{0}{\tau}}=E$$
A=E
Soit $U_C\left(t\right)=Ee^{-\frac{t}{\tau}}$
2.3. Montrer que le condensateur est déchargé à la date t = 5 τ. On considère que le condensateur est déchargé lorsque la tension uC(t) devient égale à 1% de sa valeur initiale.
$$U_C\left(t=5\tau\right)=Ee^{-\frac{5\tau}{\tau}}$$
$$U_C\left(t=5\tau\right)=Ee^{-5}$$
$$U_C\left(t=5\tau\right)=6,7.{10}^{-3}E$$
On considère que le condensateur est déchargé lorsque la tension UC(t) devient égale à 1% de sa valeur initiale.
$$U_C\left(t=5\tau\right)<{10}^{-2}E$$
Le condensateur est donc déchargé.
3. Test expérimental de la chaîne de mesure
Pour tester cette chaîne de mesure qui permet de détecter la présence d’une pression exercée sur le capteur, on réalise le circuit étudié précédemment. La commutation est réalisée automatiquement par le microcontrôleur.
On réalise l’expérience suivante :


Un premier essai est conduit sans qu’aucune pression ne soit exercée sur le capteur (figure 5). Le microcontrôleur mesure la tension uC(t) au cours du temps aux bornes du capteur capacitif.
Un second essai est réalisé au cours duquel une masse (ici un verre rempli d’eau) est posée sur le capteur (figure 6). De nouveau, on mesure la tension uC(t) au cours du temps aux bornes du capteur capacitif.
Données :
- tension du générateur idéal : E = 5 V ;
- résistance du conducteur ohmique : R = 10 MΩ ;
- épaisseur de la feuille de papier isolante sans pression : e = 1,0×10–4 m.
Les séries de mesures, obtenues lors de ces deux essais, sont présentées sur le même graphique ci-dessous (figure 7). La date t = 0 s correspond au passage du commutateur de la position 1 à 2 (figure 4).
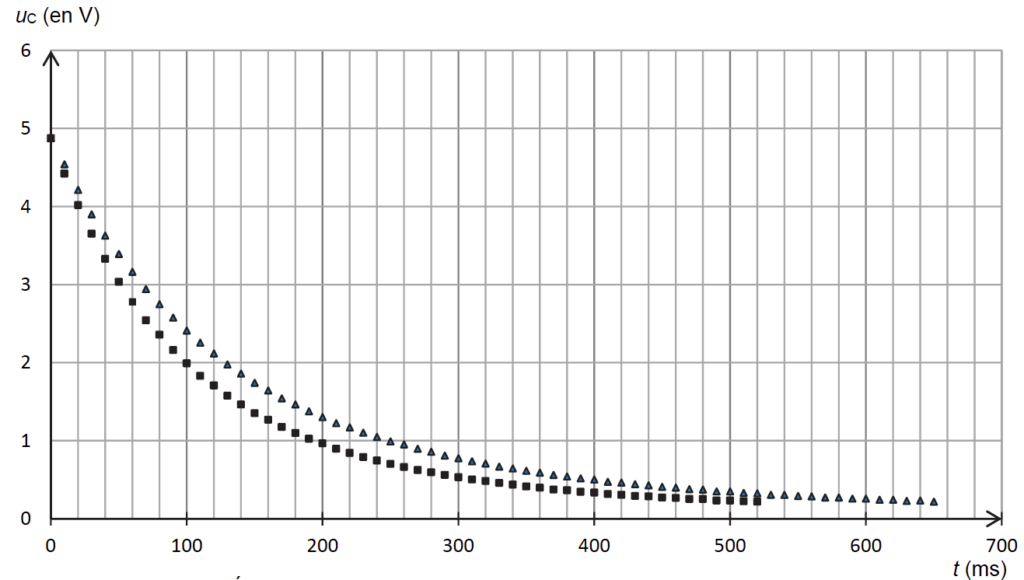
3.1. Parmi les deux séries de mesures précédentes, représentées soit par ▲ soit par ■, associer celle qui correspond au dispositif sans pression et celle qui correspond au dispositif avec pression. Justifier.
La constante de temps τ est définie par :
τ= RC
Elle peut être déterminée graphiquement par deux méthodes :
$$U_C\left(\tau\right)=Ee^{-\frac{\tau}{\tau}}=0,37E=0,37 \times 5,0=1,85\ V$$
On lit le temps pour lequel $U_C=1,85\ V$
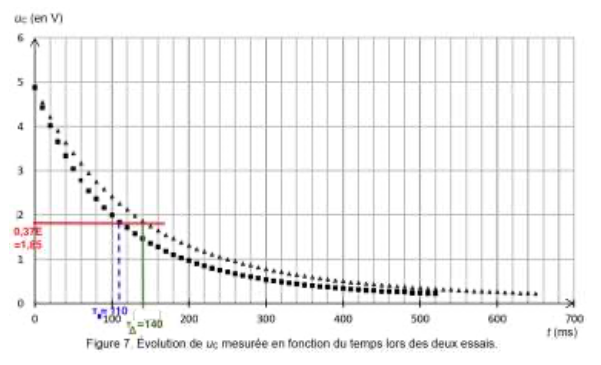
On trace la tangente à la courbe à t=0 et on regarde l’abscisse du point d’intersection entre cette tangente et l’asymptote UC=0 pour la décharge.
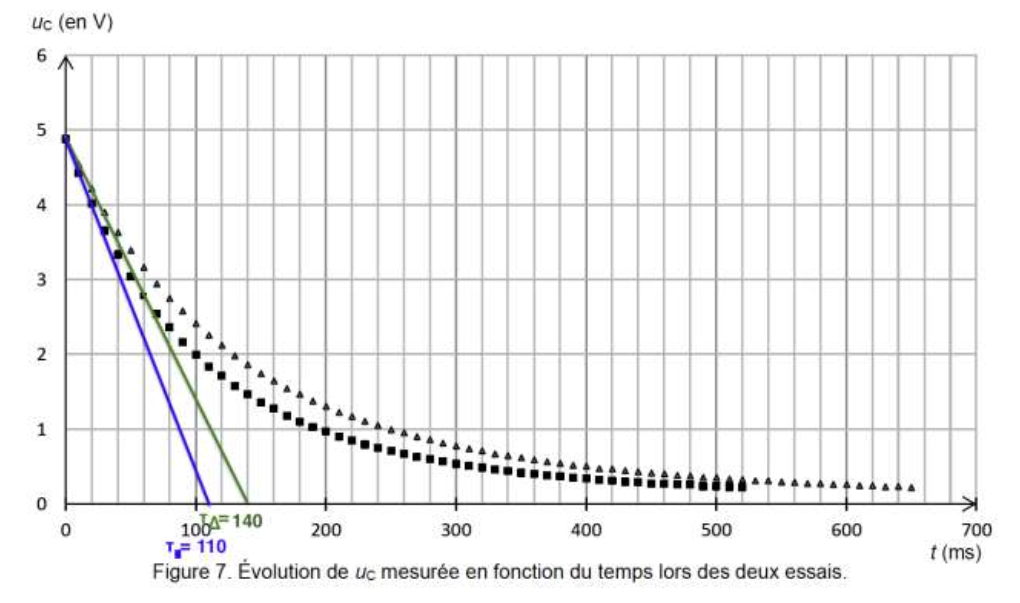
τ■<τ▲
RC■<RC▲
C■<C▲
D’après la question 1.3.
Quand un objet est posé sur le condensateur « artisanal » e diminue, ainsi C augmente car C et e sont inversement proportionnels
On en déduit donc que :
Le dispositif sans pression est ■
Le dispositif avec pression est ▲
On considère que la variation de capacité électrique ΔC est liée à la variation d’épaisseur Δe par la relation :
$\frac{\Delta C}{C}= \frac{\Delta e}{e}$
3.2. Déterminer la valeur de la variation d’épaisseur Δe, après avoir évalué la variation de capacité électrique ΔC.
Calculons la capacité C du condensateur sans pression :
$$\tau=RC$$
$$C=\frac{\tau}{R}$$
$$C=\frac{110 \times {10}^{-3}}{10 \times {10}^6}$$
$$C=1,1 \times {10}^{-8}F$$
Calculons la variation de capacité électrique ΔC :
$$\Delta C=\frac{\Delta \tau}{R}$$
$$\Delta C=\frac{140 \times {10}^{-3}-110 \times {10}^{-3}}{10 \times {10}^6}$$
$$\Delta C=3 \times {10}^{-9}F$$
Déterminons la valeur de la variation d’épaisseur Δe :
$$\frac{\Delta C}{C}=\frac{\Delta e}{e}$$
$$\frac{\Delta e}{e}=\frac{\Delta C}{C}$$
$$\Delta e=e \times \frac{\Delta C}{C}$$
$$\Delta e=1,0 \times {10}^{-4} \times \frac{3 \times {10}^{-9}}{1,1 \times {10}^{-8}}$$
$$\Delta e=2,7 \times {10}^{-5}m$$
Le dispositif est capable de détecter des petites variations d’épaisseurs.
