Bac Métropole Juin 2021 Sujet 2
Exercice B – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n° 21-PYCJ2ME2
Sujet et corrigé
Mots-clés : lentilles convergentes ; condensateur

Dans l’industrie, le contrôle qualité de l’épaisseur de matériau fabriqué est important pour respecter le cahier des charges. Plusieurs principes physiques sont utilisés pour déterminer l’épaisseur d’une plaque de métal, de verre, de films plastiques, etc.
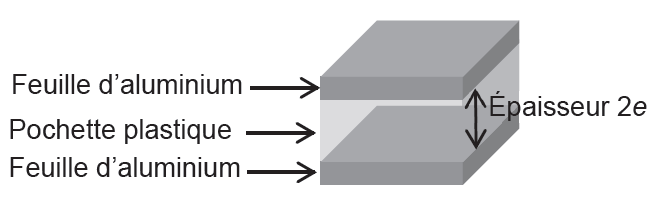
Une pochette plastique est constituée de deux films plastiques entre lesquels des documents papier peuvent être rangés. Selon les fabricants, l’épaisseur e du film plastique utilisé varie de 50 μm à 120 μm.
L’objectif de cet exercice est d’étudier deux méthodes pour déterminer l’épaisseur d’un film plastique utilisé dans la fabrication d’une pochette plastique lisse incolore.
Données :
- expression de la capacité C d’un condensateur constitué de deux armatures métalliques de surface S, exprimée en m2, séparées par une pochette plastique d’épaisseur 2e, exprimée en m : $C=1,95\times 10^{-11} \frac{ S }{2e}$
- indice de réfraction du film plastique : n = 1,49.
1. Mesure optique de l’épaisseur du film plastique
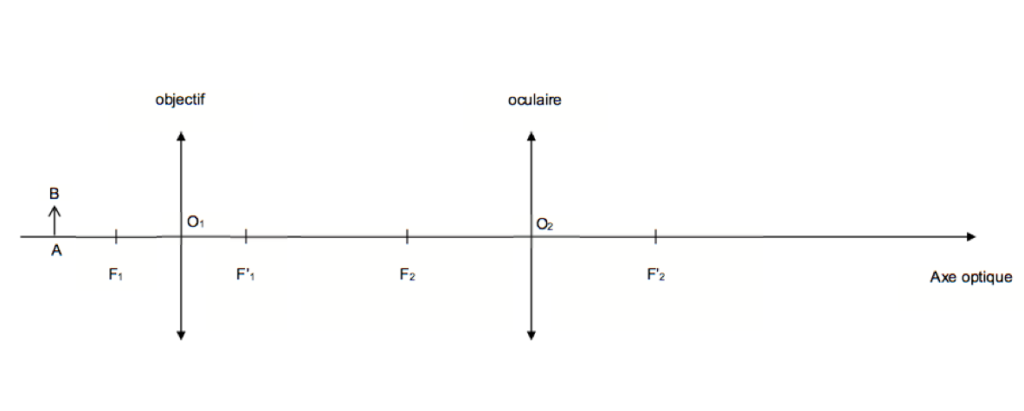
On utilise d’abord un microscope représenté en figure 1 et dont une modélisation optique est donnée en figure 2.
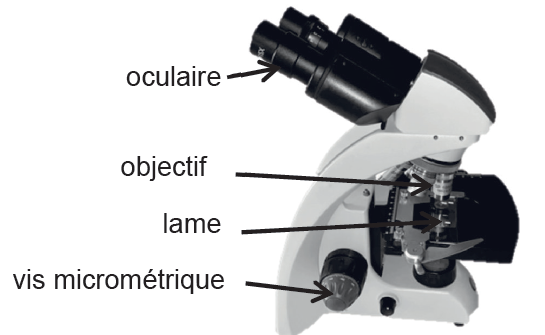
Figure 1. Photographie d’un microscope
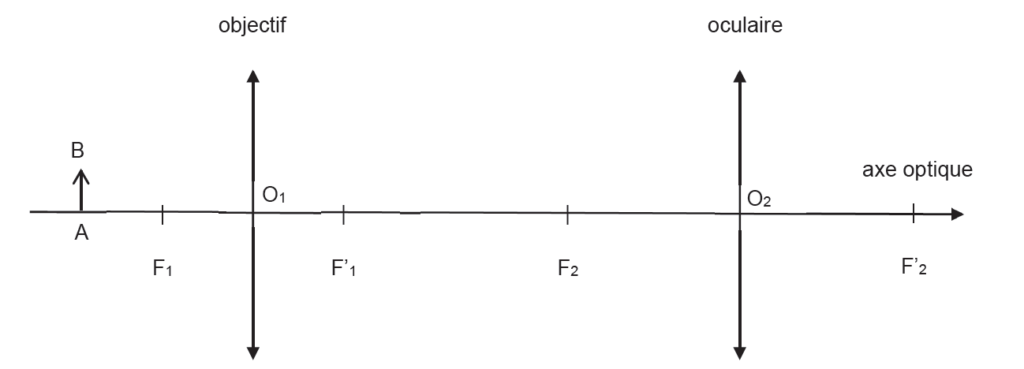
Figure 2. Modélisation d’un microscope
1.1. Sur la figure 2 reproduite dans L’ANNEXE À RENDRE AVEC LA COPIE, construire l’image intermédiaire A1B1 de l’objet AB à travers l’objectif puis l’image définitive A2B2 de A1B1 à travers l’oculaire.
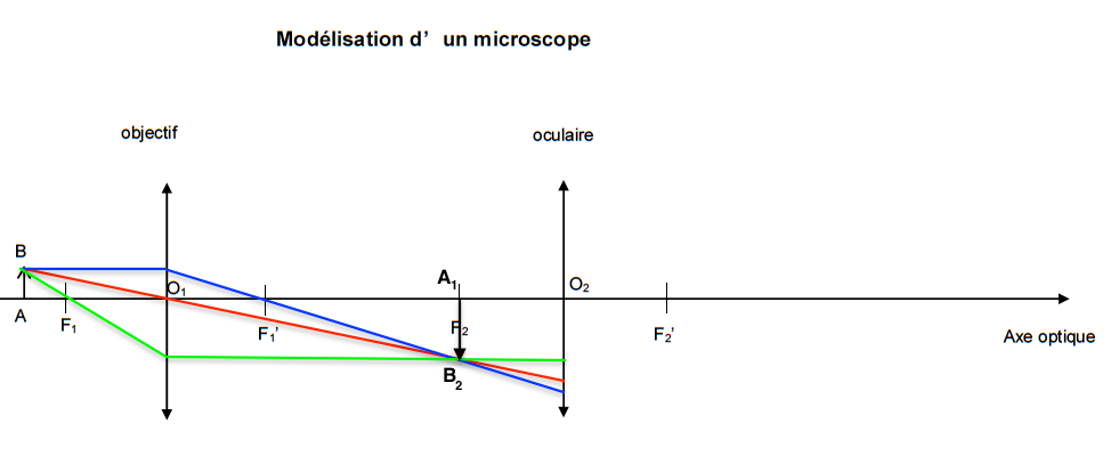
1.2. Donner les caractéristiques de l’image définitive A2B2.
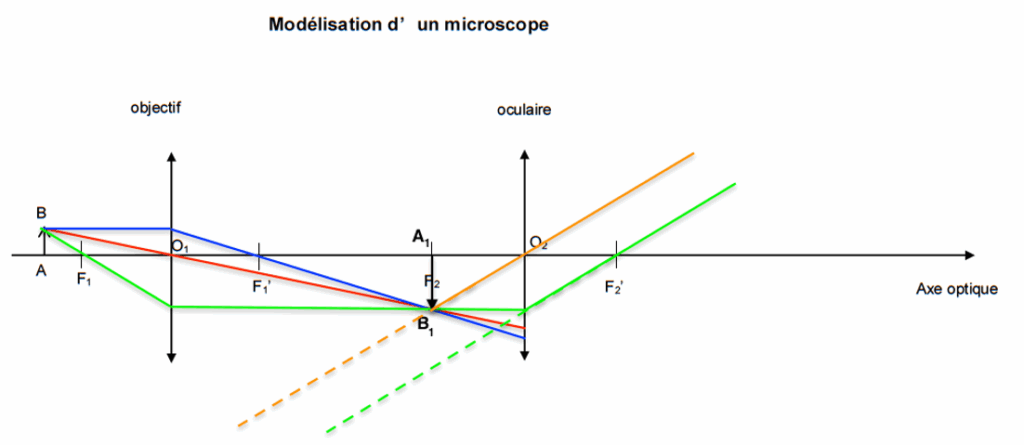
L’image définitive A2B2 est à l’infini.
1.3. Un expérimentateur désire observer l’objet à travers le microscope sans accommoder. Dans ce cas, l’image définitive A2B2 donnée par le microscope doit se situer à l’infini. Indiquer où doit se former l’image intermédiaire A1B1 pour satisfaire à cette condition.
Pour que l’image A2B2 se situe à l’infini, il faut que l’image intermédiaire A1B1 soit sur le plan focal de l’oculaire.
On trace un trait de chaque côté du film plastique et on le pose sur le microscope.
On fait successivement la mise au point sur chaque trait tracé sur le morceau de film en tournant une vis micrométrique. On photographie la vis micrométrique (figure 3). Le constructeur indique qu’un déplacement de la vis entre la graduation 0 et la graduation 10 correspond à un déplacement de 20 µm.
Photo du réglage de la vis micrométrique lors de la mise au point sur le 1er trait

Photo du réglage de la vis micrométrique lors de la mise au point sur le 2e trait

1.4. Déterminer la valeur de l’épaisseur e du film plastique sachant que le déplacement de la vis micrométrique entre ces deux mises au point est e/n. Commenter le résultat.
$$\frac{e}{n}=Déplacement$$
$$e=n \times Déplacement$$

« Le constructeur indique qu’un déplacement de la vis entre la graduation 0 et la graduation 10 correspond à un déplacement de 20 μm. »
Déplacement=(150-128)×2
$$e=1,49 \times (150-128) \times 2$$
$$e=66\ \mu m$$
Le résultat est cohérent avec les indications du fabriquant $50\mu m\ <e<120\mu m$
2. Mesure capacitive de l’épaisseur du film plastique
Pour faire une deuxième mesure de l’épaisseur du film plastique, on réalise un condensateur à l’aide de deux feuilles d’aluminium identiques de dimensions 20 cm × 20 cm entre lesquelles la pochette plastique est intercalée. Le tout est maintenu serré. Ce condensateur est utilisé dans un montage électrique dont le schéma est donné en figure 5.
Ce montage électrique est constitué d’un générateur, considéré comme une source de tension idéale qui fournit une tension E, d’un conducteur ohmique de résistance variable R et du condensateur réalisé de capacité C.
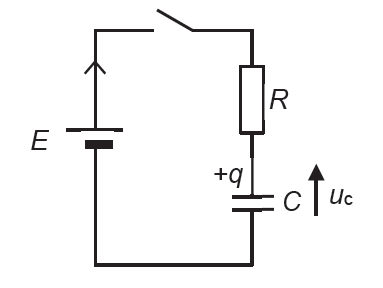
Un système d’acquisition, non représenté sur la figure 5, permet d’enregistrer l’évolution de la tension uC aux bornes du condensateur au cours du temps. À la date t = 0, on ferme l’interrupteur. Le condensateur est initialement déchargé.

2.1. Établir l’équation différentielle vérifiée par la tension aux bornes du condensateur pour t ≥ 0.
D’après la loi d’additivité des tensions ou loi des mailles :
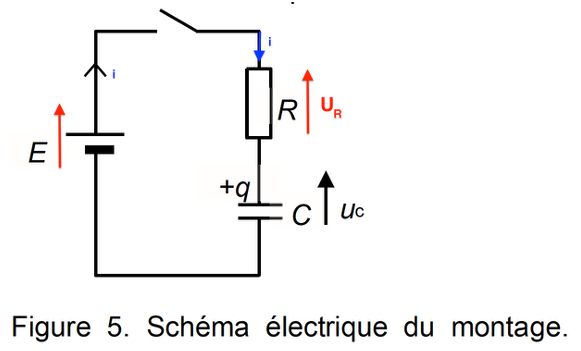
$E=U_C(t)+U_R(t)$
Or $U_R(t)=R \times i$
$E=U_C(t)+R \times i$
Or $ i(t)=\frac{dq(t)}{dt}$
$E=U_C(t)+R \times \frac{dq(t)}{dt}$
Or $q(t)=C \times U_C(t)$
$E=U_C(t)+R \times \frac{C \times U_C(t)}{dt}$
$E=U_C(t)+RC \times \frac{U_C(t)}{dt}$
2.2. La solution générale de l’équation différentielle est $u_C=Ae^{-\frac{t}{\tau}}+B $ . Déterminer l’expression des constantes A, B et τ en fonction de E, R et C.
Cette équation différentielle est satisfaite par la solution suivante :
$$U_C\left(t\right)=Ae^{- \frac{t}{\tau}}+B$$
Les constantes A et B et τ sont à déterminé.
Déterminons les constantes A et B avec les conditions initiales et finales :
condition finale le condensateur est complétement chargé :
$$U_C\left(t \rightarrow \infty \right)=E$$
Or $$U_C\left(t\rightarrow\infty\right)=Ae^{-\frac{\infty}{\tau}}+B$$
$$U_C\left(t \rightarrow \infty \right)=B$$
On à donc : B=E
condition initiale le condensateur est complétement déchargé :
$$U_C\left(t=0\right)=0$$
Or $$U_C\left(t=0\right)=Ae^{-\frac{0}{\tau}}+B=A+B=0$$
Donc A=-B=-E
On à donc :
$$U_C\left(t\right)=Ae^{-\frac{t}{\tau}}+B$$
$$U_C\left(t\right)=-Ee^{-\frac{t}{\tau}}+E$$
$$U_C\left(t\right)=E(1-e^{-\frac{t}{\tau}})$$
Déterminons τ à l’aide de l’équation :
$$U_C\left(t\right)=E(1-e^{-\frac{t}{\tau}})$$
$$\frac{dU_C}{dt}=\frac{E}{\tau}e^{-\frac{t}{\tau}}$$
$$U_C+RC\frac{dU_C}{dt}=E$$
$$E\left(1-e^{-\frac{t}{\tau}}\right)+RC \times \frac{E}{\tau}e^{-\frac{t}{\tau}}=E$$
$$E-Ee^{-\frac{t}{\tau}}+RC \times \frac{E}{\tau}e^{-\frac{t}{\tau}}=E$$
$$-Ee^{-\frac{t}{\tau}}+RC \times \frac{E}{\tau}e^{-\frac{t}{\tau}}=0$$
$$Ee^{-\frac{t}{\tau}} \times \left(-1+\frac{RC}{\tau}\right)=0$$
$$-1+\frac{RC}{\tau}=0$$
$$\frac{RC}{\tau}=1$$
$$\tau=RC$$
D’où
$$U_C(t)=E(1-e^{-\frac{t}{RC}})$$
2.3. Déterminer la valeur de la constante B et la valeur du temps caractéristique τ à l’aide de la figure 6 en expliquant la démarche suivie.
Graphiquement :
$$U_C\left(t\rightarrow\infty\right)=E=6,0V$$
$\tau$ peut être déterminée graphiquement par deux méthodes :
$$U_C\left(\tau\right)=E\left(1-e^{-\frac{\tau}{\tau}}\right)=E\left(1-e^{-1}\right)=0,63E=0,63 \times 6,0=3,78V$$
On lit le temps pour lequel $U_C=3,78V$
On trace la tangente à la courbe à t=0 et on regarde l’abscisse du point d’intersection entre cette tangente et l’asymptote $U_C=E $ pour la charge.
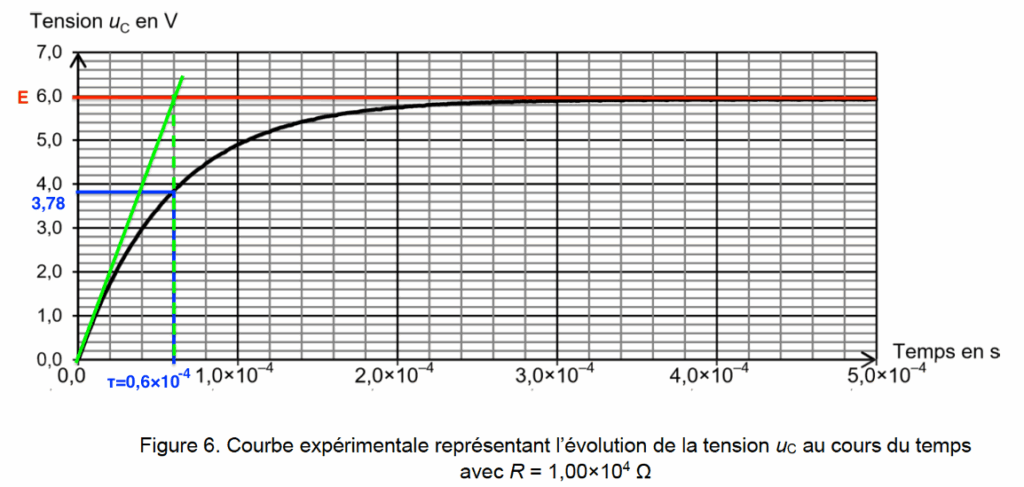
$$\tau=0,6{ \times 10}^{-4}s$$
2.4. Déterminer la valeur de la capacité C du condensateur réalisé.
$$C=\frac{\tau}{R}$$
$$C=\frac{0,6{ \times 10}^{-4}}{1,0{ \times 10}^4}$$
$$C=0,6{ \times 10}^{-8}F$$
2.5. En déduire la valeur de l’épaisseur du film plastique utilisé pour fabriquer la pochette. Commenter le résultat.
$$C=1,95{ \times 10}^{-11} \times \frac{S}{2e}$$
$$e=1,95{ \times 10}^{-11} \times \frac{S}{2C}$$
$$e=1,95{ \times 10}^{-11} \times \frac{20{ \times 10}^{-2} \times 20{ \times 10}^{-2}}{2 \times 0,6{ \times 10}^{-8}}$$
$$e=6,5{ \times 10}^{-6}=65\ \mu m$$
Le résultat est cohérent avec les indications du fabriquant $50\mu m\ <e<120\mu m$
De plus cette valeur est cohérente avec la valeur trouvée à la question 1.4
Modélisation d’un microscope