Aspects énergétiques des phénomènes mécaniques : Le ski de vitesse

E3C2 – 10 points – Durée 1h – calculatrice autorisée

Aspects énergétiques des phénomènes mécaniques : Le ski de vitesse (10 points)

Personne sur Terre, et sans assistance motorisée, ne va plus vite que l’Italien Simone Origone, leader d’une discipline à part du ski alpin, plus spectaculaire que dangereuse.

TamTam Photo

Impossible 252,632 km/h ? Et pourtant. C’est bien la vitesse atteinte vendredi 3 avril 2015 par Simone Origone qui, pour y parvenir, s’est servi d’un instrument complexe : une paire de skis. Et d’un moteur surpuissant : la gravité.

En se laissant tomber du haut de la piste de Chabrières, gigantesque toboggan enneigé qui servait cette semaine de scène au Speed Masters dans la station de Vars (Hautes-Alpes), l’Italien de 35 ans a battu son propre record du monde de vitesse à ski (252,454 km/h).

Le Monde | 03.04.2015

Données :

caractéristiques techniques de la piste de Chabrières considérée comme rectiligne :
altitude de départ (D) : z_D= 2720 m ;
altitude d’arrivée (A) : z_A = 2285 m ;
pente moyenne α = 24° ;
longueur de la piste : L = 1070 m.
caractéristiques du skieur Simone Origone :
masse : 87 kg ;
équipement : 15 kg.
intensité de la pesanteur g = 9,8 m.s^-2.

Partie 1 : étude énergétique du mouvement du skieur dans l’hypothèse de frottement négligeable

Le système étudié est le « skieur » constitué de l’athlète avec son équipement de masse totale m et de centre de masse G en mouvement sur la piste de ski d’un point D d’altitude z_D à un point A d’altitude z_A.

Le départ s’effectue sans vitesse initiale. Le référentiel d’étude est supposé galiléen. Dans cette partie les frottements subis par le système sont négligés devant les autres actions mises en jeu.

1.1. Effectuer le bilan des actions, modélisées par des forces, agissant sur le système. Préciser le sens et la direction de chaque force.

Bilan des forces : le Poids et la réaction du sol. Les frottements sont négligés.

Forces	Direction	Sens
Poids	Verticale	Vers le bas
Réaction du sol	Perpendiculaire au support	Vers le haut

1.2. Calculer le travail W_DA de chaque force entre le point de départ D et le point d’arrivée A.

Travail du poids :

$W_{DA}\left(\vec{P}\right)=mg\ (Z_D-Z_A)$

$W_{DA}\left(\vec{P}\right)=(87+15)\times 9,8\times (2720\ -2285\ )$

$W_{DA}\left(\vec{P}\right)=4,3.10^5J$

Travail de la réaction du sol:

$W_{DA}\left(\vec{R}\right)=\vec{R}.\vec{DA}$

$W_{DA}\left(\vec{R}\right)=0\ J$

Car

$\vec{R}\ et\ \vec{DA}$

sont perpendiculaires.

1.3. En utilisant le théorème de l’énergie cinétique, déduire la valeur de la vitesse à l’arrivée, notée v_A, en m.s^-1 puis en km.h^-1.

Théorème de l’énergie cinétique :

$\Delta E_{C} =\Sigma W_{DA}\left(\vec{F}\right)$

$E_{C(A)}-E_{C\left(D\right)}=W_{DA}\left(\vec{P}\right)+W_{DA}\left(\vec{R}\right)$

$\frac{1}{2}m.v_A^2-\frac{1}{2}m.v_D^2=W_{DA}\left(\vec{P}\right)$

Or v_D=0 m.s^-1 car il part de D sans vitesse initiale

$\frac{1}{2}m.v_A^2=W_{DA}\left(\vec{P}\right)$

$v_A^2=\frac{2}{m}W_{DA}\left(\vec{P}\right)$

$v_A=\sqrt{\frac{2}{m}W_{DA}\left(\vec{P}\right)}$

$v_A=\sqrt{\frac{2}{(87+15)}\times 4,3.10^5}=92\ m.s^{-1}=331\ Km.h^{-1}$

Pour passer une vitesse de m.s^-1 à Km.h^-1 , on multiplie le résultat par 3,6

1.4. Cette valeur est-elle en accord avec celle de la vitesse atteinte le vendredi 3 avril 2015 par Simone Origone ? Quel aspect de la modélisation effectuée doit être remis en cause ?

Cette valeur (331 km/h) est tres superieure à celle mesurée (252,632 km/h). Cette différence s’explique car nous avons négligé les forces de frottements dans cette modélisation.

Partie 2 : mouvement d’un mobile autoporteur

On se propose de mesurer l’intensité des actions de frottements qui agissent sur un mobile en mouvement. Ces actions seront modélisées par une force constante f^→, d’intensité f, et de sens opposé au vecteur vitesse.

Ce mobile, de centre de masse G, de masse m = 220 g, est abandonné sans vitesse sur un plan incliné d’un angle α₀par rapport à l’horizontale. Au cours de son mouvement, le mobile suit la ligne de plus grande pente de direction Ax, la position de G est repérée en fonction du temps par sa coordonnée x dans le repère (A, ). On peut se référer à l’annexe 1 à rendre avec la copie.

Une vidéo du mouvement est réalisée. Un logiciel de pointage permet de relever les valeurs de la position x et de l’altitude z sur l’axe vertical Oz du centre d’inertie G à des intervalles de temps réguliers et de déterminer à chaque pointage la valeur de la vitesse du mobile le long de l’axe Ax. On peut se référer à l’annexe 1 à rendre avec la copie.

Un programme python (annexe 2 à joindre avec la copie) permet de représenter l’évolution de l’énergie cinétique du système au cours du temps.

On obtient la courbe ci-dessous.

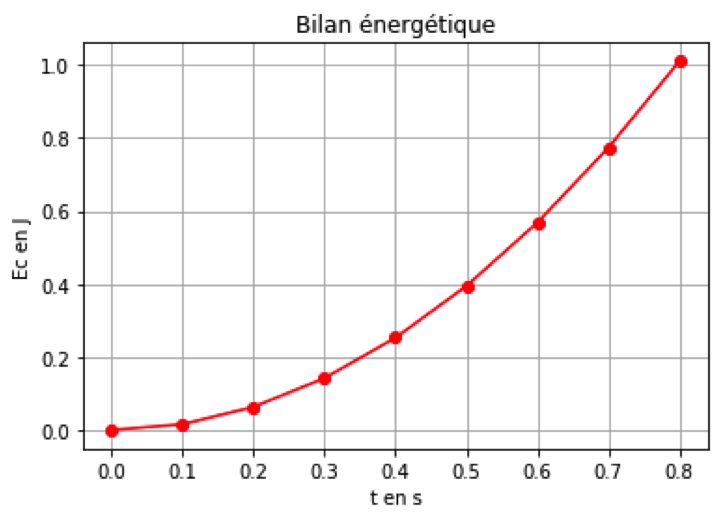
2.1. Modifier le script du programme de l’annexe 2 à rendre avec la copie en ajoutant une ligne de code (ligne 14) qui permettra de déterminer la valeur de l’énergie potentielle E_pp du système. Quelle donnée faut-il ajouter au script ? Compléter alors la ligne 5.

L’énergie potentielle : Epp=mgz

Il faut donc entré la formule de l’énergie potentielle (ligne 14) et la valeur de g (ligne 5).

5 g=9.8 # valeur de g en m.s^-2

14 Epp=[m*g*z for z in alt] # crée la liste Epp

Le script est ensuite encore modifié pour faire apparaître l’énergie cinétique, l’énergie potentielle et l’énergie mécanique. On obtient les courbes ci-dessous. L’énergie potentielle de pesanteur est choisie nulle en O.

Énergie cinétique Ec(●)

Énergie potentielle Epp(▼)

Énergie mécanique Em(*)

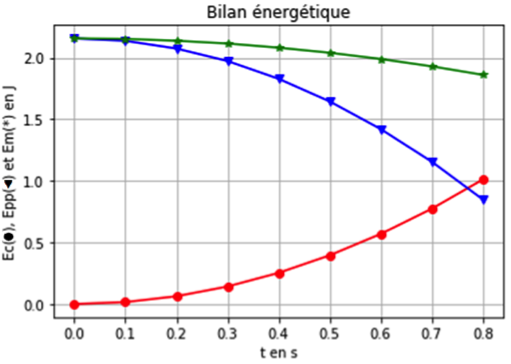
2.2. Comment expliquer l’évolution de l’énergie mécanique au cours du temps ?

L’énergie mécanique diminue à cause du temps à cause des frottements.

2.3. Compléter le schéma de l’annexe 1 à rendre avec la copie en représentant les forces modélisant les actions sur le système.

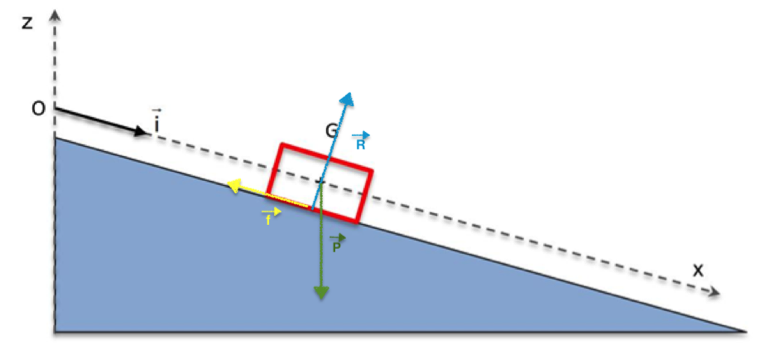
2.4. En tenant compte des valeurs relevées dans le tableau de l’annexe 1 à rendre avec la copie, calculer les valeurs de l’énergie mécanique Em₀ et Em₈ respectivement aux instants t₀ = 0,000 s et t₈ = 0,800 s.

$E_{m(0)}=E_{C\left(0\right)} + E_{pp(0)}$

$E_{m(0)}=\frac{1}{2}m.v_0^2 + mgz_{0}$

$E_{m(0)}=\frac{1}{2}\times 220.10^{-3}\times 0^2 + 220.10^{-3}\times 9,8 \times 1,000$

$E_{m(0)}=2,2 J$

$E_{m(8)}=E_{C\left(8\right)} + E_{pp(8)}$

$E_{m(8)}=\frac{1}{2}m.v_8^2 + mgz_{8}$

$E_{m(8)}=\frac{1}{2}\times 220.10^{-3}\times 3,0312^2 + 220.10^{-3}\times 9,8 \times 0,394$

$E_{m(8)}=1,9 J$

2.5. À l’aide d’une bilan énergétique, montrer que dans le cadre de ce modèle :

$f=\frac{E_{m0}-E_{m8}}{x_8-x_0}$

où x₈ =x (t = 0,800 s) et x₀= x(t = 0,000 s).

Théorème de l’énergie mécanique :

$\Delta E_m=\Sigma W_{AB}(\vec{F}_{non\ conservatives})$

$E_{m(8)}-E_{m(0)}=W_{8\rightarrow 0}(\vec{f})$

$E_{m(8)}-E_{m(0)}=f\times ({x_8-x_0})\times cos(\alpha)$

$E_{m(8)}-E_{m(0)}=f\times ({x_8-x_0})\times -1$

$f=\frac{E_{m0}-E_{m8}}{x_8-x_0}$

$f=\frac{2,2-1,9}{1,212-0}=0,25N$

2.6. Déterminer la valeur de l’intensité de la force modélisant les frottements s’exerçant sur le mobile. Commenter.

Comparons cette force au poids :

P=mg

$P=220.10^{-3}\times 9,8=2,0\ N$

$\frac{P}{f}=\frac{2,0}{0,25}=8$

P est 8 fois plus grand que f.

f n’est pas négligeable devant P.

Partie 3 : retour qualitatif sur l’étude énergétique du mouvement du skieur

3. Quelles sont les causes des actions de frottement exercées sur le skieur ? Discuter de l’influence de la valeur de la vitesse et de la pertinence d’une modélisation de ceux-ci par une force d’intensité constante.

Les causes des actions de frottement exercées sur le skieur :

Frottement de l’air qui dépend de la vitesse
Frottement des skis sur la piste

La vitesse n’étant pas constante, la force de frottement ne le sera pas non plus. Ainsi, il n’est pas pertinent de modéliser la force de frottement par une force d’intensité constante.

Annexe 1 à rendre avec la copie

*Numéro*	t(s)	x(m)	v(m.s⁻¹)	z(m)
0	0.000	0.000	0.000	1.000
1	0.100	0.019	0.3789	0.991
2	0.200	0.076	0.7578	0.962
3	0.300	0.171	1.1367	0.915
4	0.400	0.303	1.5156	0.848
5	0.500	0.474	1.8945	0.763
6	0.600	0.682	2.2734	0.659
7	0.700	0.928	2.6523	0.536
8	0.800	1.212	3.0312	0.394

Annexe 2 à rendre avec la copie

1 import matplotlib.pyplot as plt

3 m = 0.220 # valeur de m en kg

4 alpha = 0.2618 # valeur de alpha en radian

7 # liste des dates relevées, des positions, des vitesses et des altitudes

8 tps = [0.000, 0.100, 0.200, 0.300, 0.400, 0.500, 0.600, 0.700, 0.800]

9 pos = [0.000, 0.019, 0.076, 0.171, 0.303, 0.474, 0.682, 0.928, 1.212]

10 vit = [0.000, 0.3789, 0.7578, 1.1367, 1.5156, 1.8945, 2.2734, 2.6523, 3.0312]

11 alt = [1.000, 0.991, 0.962, 0.915, 0.848, 0.763, 0.659, 0.536, 0.394]

13 Ec = [1/2*m*v**2 for v in vit] # crée la liste Ec

18 plt.grid(True)

19 plt.plot(tps,Ec, »red »)

23 plt.xlabel(« t en s »)

24 plt.ylabel(« Ec en J »)

26 plt.title(« Bilan énergétique »)

28 plt.show()