Accélérateur linéaire Linac2 du CERN

Sujet zéro 2

Exercice B – (5 points) –  au choix du candidat – Durée 0h53 – Calculatrice autorisée

EXERCICE B – Accélérateur linéaire Linac2 du CERN (5 points)

Mots clés : mouvement d’une particule chargée dans un champ électrique uniforme, accélérateur de particules chargées.

L’accélérateur linéaire « Linac2 » permet de communiquer une vitesse importante aux protons que les chercheurs utilisent ensuite dans les expériences menées au laboratoire européen pour la physique des particules (CERN) afin d’explorer la structure de la matière. Les protons, initialement au repos, atteignent l’énergie de 50 MeV à la sortie de l’accélérateur. Ils pénètrent alors dans le « Synchrotron injecteur », le maillon suivant de la suite d’accélérateurs du CERN, qui les porte à une énergie encore plus élevée.

D’après : https://home.cern/fr/science/accelerators/linear-accelerator-2 .

Données

• Charge du proton : e = 1,6×10^-19 C.
• Masse du proton : m_p= 1,67×10^-27 kg.
• Champ de pesanteur terrestre : g = 9,81 mžs^-2.
• 1 eV = 1,6×10^-19 J.
• 1 MV = 10⁶ V.

« Linac2 » est un accélérateur linéaire dans lequel les protons passent par une succession de zones modélisables par des condensateurs plans et où règne un champ électrique et de zones où ne règne aucun champ électrique. Dans une première partie, l’étude porte sur l’accélération initiale des protons par un condensateur plan, puis dans une seconde partie, sur le principe des accélérations successives des protons dans le « Linac2 ».

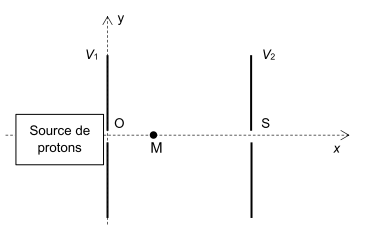
Un proton entre dans le condensateur plan avec une vitesse initiale nulle en O (figure 1). Une tension électrique positive U = V₁ – V₂ est appliquée entre les plaques du condensateur séparées d’une distance d.

Le champ électrique créé entre les plaques est supposé uniforme, dirigé dans le sens de l’axe Ox et de norme .

Les plaques sont percées en O et S pour laisser passer les protons.

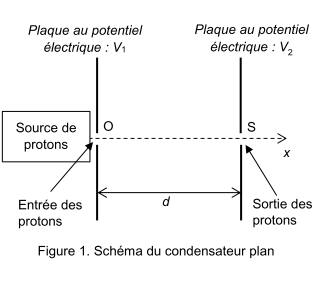
Figure 1. Schéma du condensateur plan

Caractéristiques du condensateur :

• distance entre les plaques : d = 10,0 cm ;
• tension électrique appliquée : U = V₁ – V₂ = 2,00 MV.

Le mouvement du proton dans le condensateur est étudié dans le référentiel terrestre supposé galiléen.

1.1. Représenter, sur le document de l’ANNEXE À RENDRE AVEC LA COPIE, le vecteur champ électrique au point M. Échelle : 1 cm représente 10 MVžm^-1.

1.2. Comparer la valeur du poids d’un proton avec celle de la force électrique à laquelle il est soumis à l’intérieur du condensateur. Conclure.

1.3. Déterminer l’expression du vecteur accélération du proton en fonction de m_p , e, . En déduire la nature de son mouvement dans le condensateur.

1.4. En appliquant le théorème de l’énergie cinétique, montrer que la variation d’énergie cinétique du proton entre le point d’entrée O et le point de sortie S du condensateur est égale à :

E_C(S) – E_C(O) = eU.

1.5. En déduire l’expression de la vitesse v_S du proton à la sortie du premier condensateur en S en fonction de m_p , e et U. Déterminer sa valeur et commenter le résultat.

2. Principe du Linac2 – accélérateur linéaire

Dans une enceinte où règne un vide poussé, on fait passer les protons dans une série de tubes métalliques reliés alternativement à l’une ou à l’autre des bornes d’un générateur de tension alternative Ua(t) (voir figure 2). Cette tension crée, dans les intervalles qui séparent les tubes, un champ électrique dans la direction de l’axe Ox.

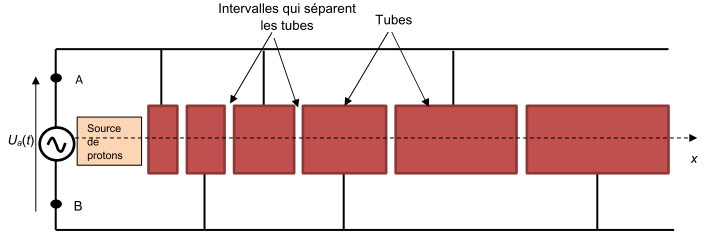
Figure 2. Schéma simplifié du Linac 2.

Le champ électrique régnant dans les intervalles étant variable au cours du temps, la fréquence de la tension Ua(t) et la longueur des tubes sont choisies très précisément pour que les protons arrivent dans chaque intervalle à l’instant où le sens du champ est tel qu’il permet leur accélération. On considère qu’à l’intérieur des tubes le champ électrique est nul et donc que les particules s’y déplacent à vitesse constante (figure 3).

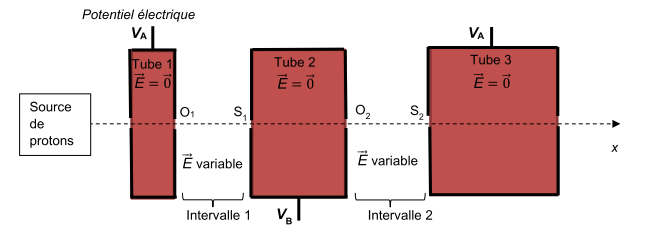
Figure 3. Schéma des deux premiers intervalles (l’échelle n’est pas respectée).

L’énergie cinétique des protons augmentant au passage dans chaque intervalle, l’énergie cinétique atteinte à la sortie de l’accélérateur dépend, entre autres, du nombre de tubes.

L’un des intérêts d’un tel dispositif est qu’il suffit d’ajouter des tubes ou d’augmenter la valeur du champ électrique pour augmenter l’énergie cinétique finale des protons. Son principal inconvénient est son encombrement qui est, pour le Linac2, une longueur de 34 m.

Chaque intervalle se comporte comme le condensateur plan étudié dans la première partie (figure 1).

Le générateur produit une tension sinusoïdale de période T = 40 ns. On donne la courbe de variation de la tension Ua en fonction du temps (figure 4). Si Ua(t) > 0, alors V_A > V_B et si Ua(t) < 0 alors V_A < V_B.

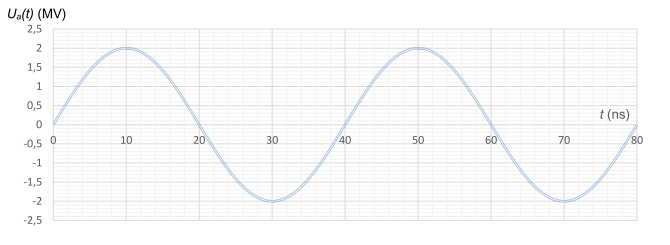
Figure 4. Évolution de la tension électrique Ua(t) délivrée par le générateur.

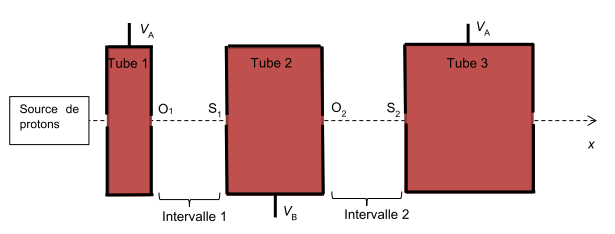
2.1. Indiquer le sens du champ électrique qui règne dans l’intervalle 1 et dans l’intervalle 2 entre les tubes à l’instant t = T/4 . Représenter, sans soucis d’échelle, le vecteur champ électrique dans l’intervalle 1 et celui dans l’intervalle 2 sur le schéma de l’ANNEXE À RENDRE AVEC LA COPIE.

2.2. Mêmes questions à la date .

2.3. Pour être accélérés de manière optimale dans chaque intervalle, les protons doivent mettre une durée pour traverser chaque tube. Justifier cette affirmation.

2.4. Expliquer qualitativement pourquoi les tubes du Linac2 sont de plus en plus longs.

ANNEXE À RENDRE avec la copie de l’exercice B Accélérateur linéaire Linac2 du CERN

Annexe de la question 1.1 :

Annexe de la question 2.1. :