A la découverte de Saturne

Bac Métropole mars 2023 Sujet 1

Exercice 1 – (11 points) –  Durée 1h56 – Calculatrice autorisée

Sujet n°23-PYCJ1ME1

EXERCICE 1 – À LA DÉCOUVERTE DE SATURNE (11 points)

La planète Saturne a été observée à travers une lunette astronomique pour la première fois par l’astronome Galilée en 1610. Il a pu entrevoir la planète, mais sa lunette ne lui a pas permis de distinguer clairement ce qui l’entourait (figure 1).

Ce n’est qu’en 1655, grâce à une lunette plus perfectionnée, que Christian Huygens comprend que ce qui entoure Saturne sont des anneaux dont l’aspect varie avec l’angle d’observation. La même année, il découvre également Titan, le plus gros satellite de Saturne (figures 2 et 3).

Source : Systema Saturnium de Huygens

Le but de cet exercice est d’étudier la lunette astronomique de Huygens afin de comparer ses observations de Saturne et de ses anneaux à celles de Galilée. La fin de l’exercice est consacrée à l’étude du mouvement du satellite Titan à partir des observations de Huygens.

Données :

• caractéristiques des lunettes astronomiques utilisées par Galilée et Huygens :

	Distance focale f1‘ de l’objectif	Distance focale f2‘ de l’oculaire	Diamètre a de l’objectif	Grossissement
Lunette de Galilée utilisée en 1610			29,0 mm	GGal = 14
Lunette de Huygens utilisée en 1655	329 cm	7,0 cm	51,0 mm

• un observateur peut distinguer deux points différents d’un objet si l’angle sous lequel sont vus ces deux points, depuis le point d’observation, est supérieur ou égal à 3,0×10^-4 rad ;
• approximation dans le cas de petits angles (θ << 1 rad) : tan (θ) = θ ;
• constante de gravitation universelle : G = 6,67×10^-11 N·m²·kg^-2 ;
• masse de Saturne : M_S = 5,68×10²⁶ kg ;
• masse de Titan : M_T = 1,34×10²³ kg ;
• distance moyenne entre la Terre et Saturne : D_T-S = 1,42×10⁹ km ;
• rayon de l’orbite de Titan autour de Saturne : R = 1,22×10⁶ km.

1.   Observation de Saturne par Huygens

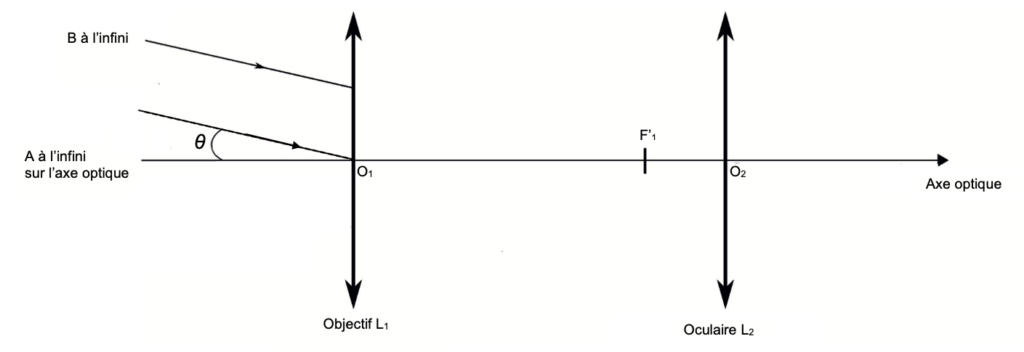
La lunette de Huygens, considérée comme afocale, est modélisée par un système de deux lentilles minces convergentes notées L₁ et L₂. La lentille L₁ représente l’objectif et la lentille L₂ l’oculaire. Leurs centres optiques respectifs sont notés O₁ et O₂ et leurs distances focales respectives sont notées f₁‘ et f₂‘.

Sur la figure A1 de l’ANNEXE À RENDRE AVEC LA COPIE, réalisée sans souci d’échelle, sont représentées les deux lentilles et la position du foyer image F₁’ de la lentille L₁. La lunette est utilisée pour observer un objet AB, supposé « à l’infini », dont l’image par l’objectif sera notée A₁B₁. Deux rayons lumineux issus de B sont représentés sur le schéma.

Q1. Préciser le sens du terme « afocal ».

Un système optique est dit afocal s’il donne d’un objet à l’infini une image à l’infini.

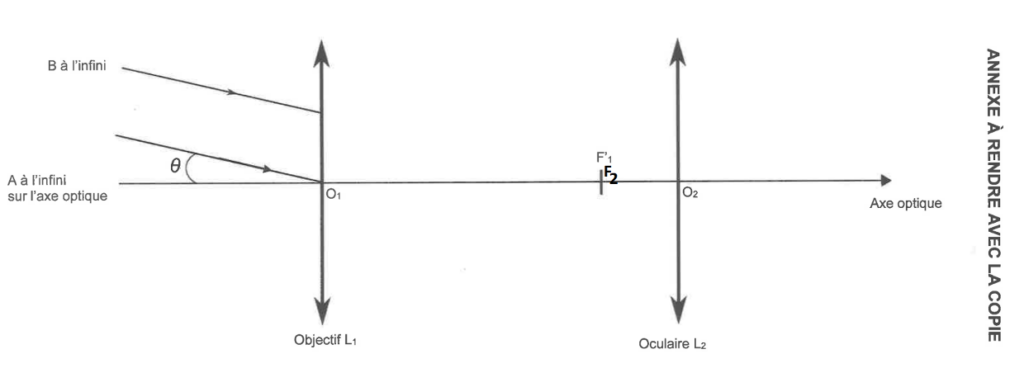
Q2. Placer, sur la figure A1 de l’ANNEXE À RENDRE AVEC LA COPIE, les foyers objet F₂ et image F₂’ de la lentille L₂ dans le cas d’une lunette afocale.

La lentille L1, donne de l’objet $A_\infty B_\infty$, une image $A_1B_1$ sur le foyer image $F_1^\prime$.
Pour que la lentille L2, donne de l’objet $A_1B_1$, une image à l’infini, il faut que celui-ci soit sur le foyer $F_2$.
Ainsi, les deux foyers $F_1^\prime$ et $F_2$ sont confondus.

Q3. Construire, sur la figure A1 de l’ANNEXE À RENDRE AVEC LA COPIE, la marche des deux rayons lumineux issus de B qui émergent de la lunette en faisant apparaître l’image intermédiaire A₁B₁.

La lentille L1, donne de l’objet $A_\infty B_\infty$, une image $A_1B_1$ sur le plan focal.
Le rayon issu de B, passant par $O_1$ n’est pas dévié.
Le point $B_1$ est défini par l’intersection de ce rayon et le plan focal.

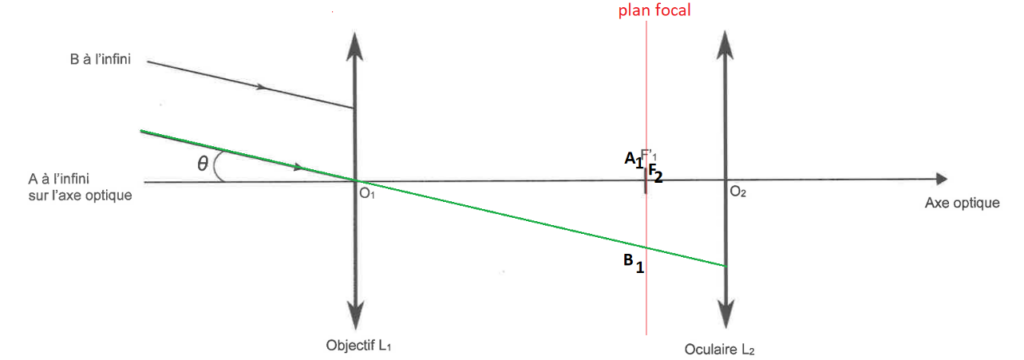
L’autre rayon est parallèle au premier. Il est dévié vers le point $B_1$.

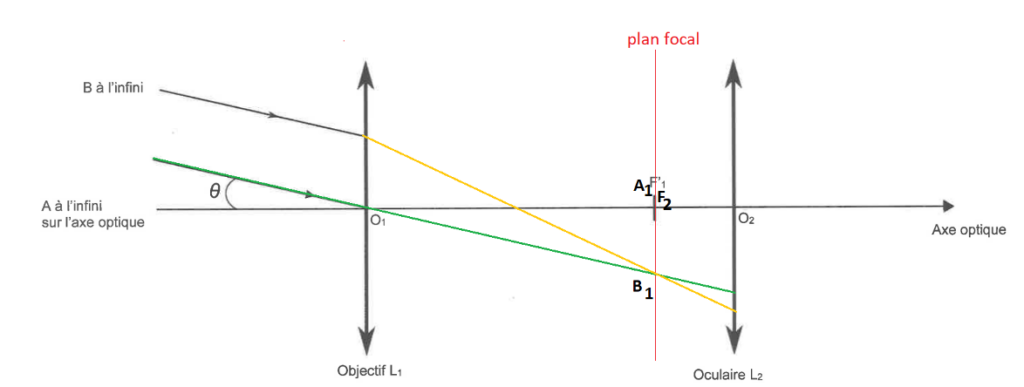
Un rayon issu de $B_1$ passant par $O_2$ n’est pas dévié.

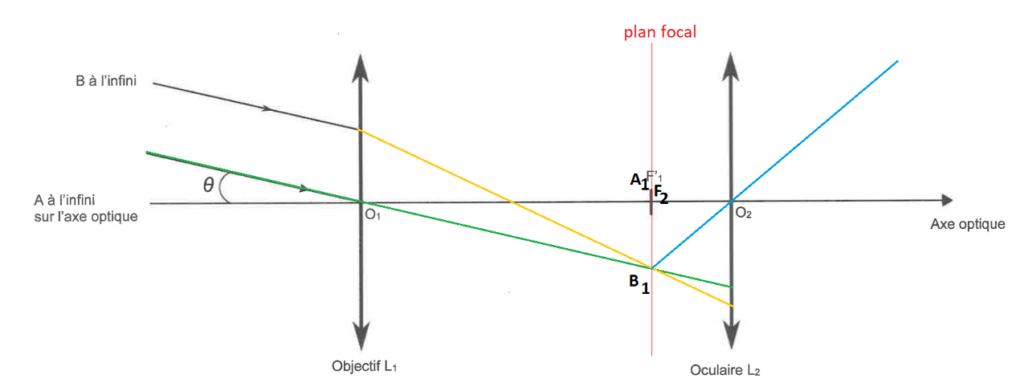
$A_1B_1$ étant sur le plan focal, il donnera une image à l’infini, tous les rayons issus de $B_1$, passant par la lentille L2 seront parallèles.

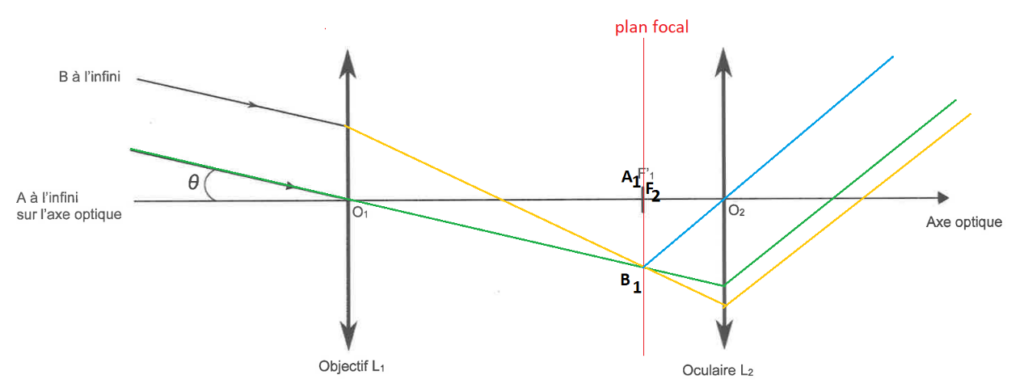
La lunette de Huygens est constituée d’un tube long de 372 cm. Comme indiqué sur la figure 4, l’oculaire est placé à une extrémité du tube. L’objectif quant à lui est enfoncé de 36 cm par rapport à l’autre extrémité, afin de le protéger de la buée.

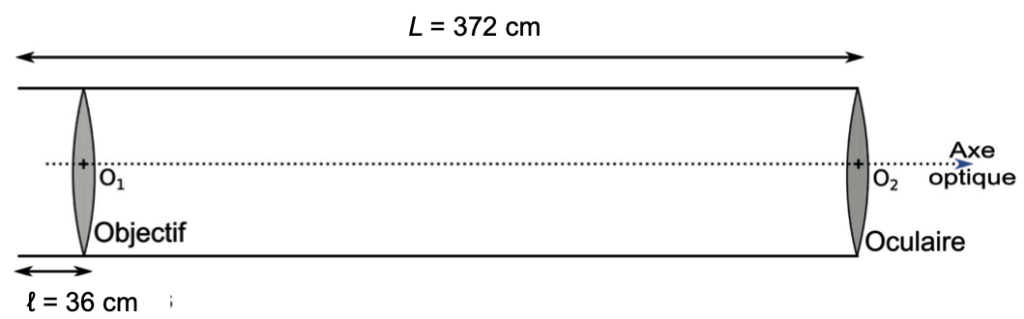
Figure 4. Représentation schématique de la lunette de Huygens (échelle non respectée)

Q4. Vérifier, à partir des données, que la lunette d’Huygens peut être considérée comme « afocale ».

Le système optique est dit afocal si les deux foyers $F_1^\prime$ et $F_2$ sont confondus donc si
$$
O_1O_2=f_1^\prime+f_2^\prime
$$

D‘après la représentation :
$$
O_1O_2=L-l
$$
$$
O_1O_2=372-36
$$
$$
O_1O_2=336\ cm
$$

Or
$$
f_1^\prime+f_2^\prime=329+7,0
$$
$$
f_1^\prime+f_2^\prime=336\ cm
$$

On a donc : $O_1O_2=f_1^\prime+f_2^\prime$
La lunette d’Hygens peut être considérée comme « afocale »

L’angle q, représenté sur la figure A1 de l’ANNEXE À RENDRE AVEC LA COPIE, désigne l’angle sous lequel l’espace AB entre la surface de Saturne et son premier anneau est vu à l’œil nu depuis la Terre, lorsque les anneaux de Saturne sont vus de face (voir figure 5).

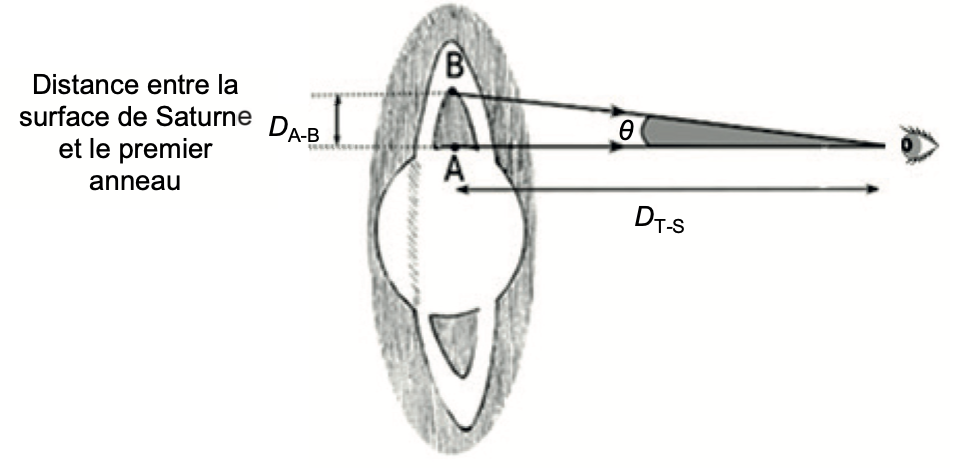
Figure 5. Angle sous lequel Saturne est vue par Huygens sans la lunette (échelle non respectée)

On note θ’ l’angle sous lequel un observateur voit l’image A’B’ de l’espace AB, à travers la lunette astronomique.

Q5. Placer l’angle θ’ sur la figure A1 de l’ANNEXE À RENDRE AVEC LA COPIE.

$\theta^\prime$ est l’angle sous lequel est vue l’image finale en sortie de lunette.

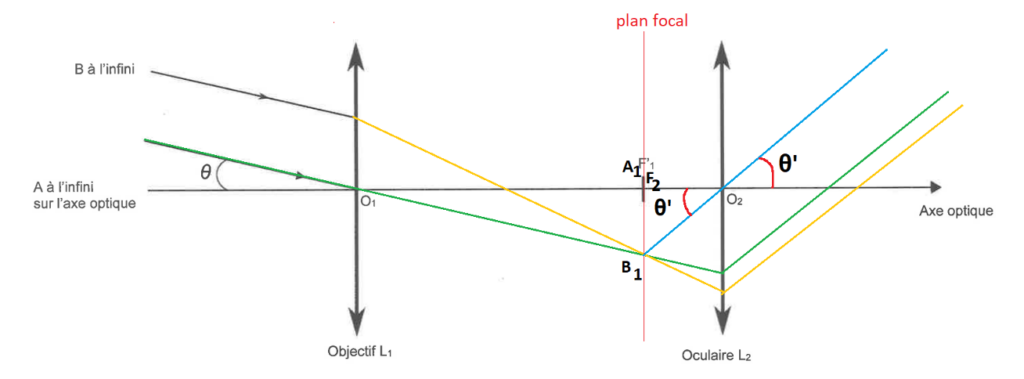
Q6. Donner l’expression du grossissement G_Huy de la lunette de Huygens en fonction des angles θ et θ’.

Le grossissement G_Huy est défini par :
$$
G_{Huy}=\frac{\theta^\prime}{\theta}
$$

Q7. Montrer que le grossissement G_Huy de la lunette de Huygens s’exprime en fonction des distances focales des lentilles L₁ et L₂ constituant la lunette :

$$G_{\mathrm{Huy}}=\frac{f_1^\prime}{f_2^\prime}$$

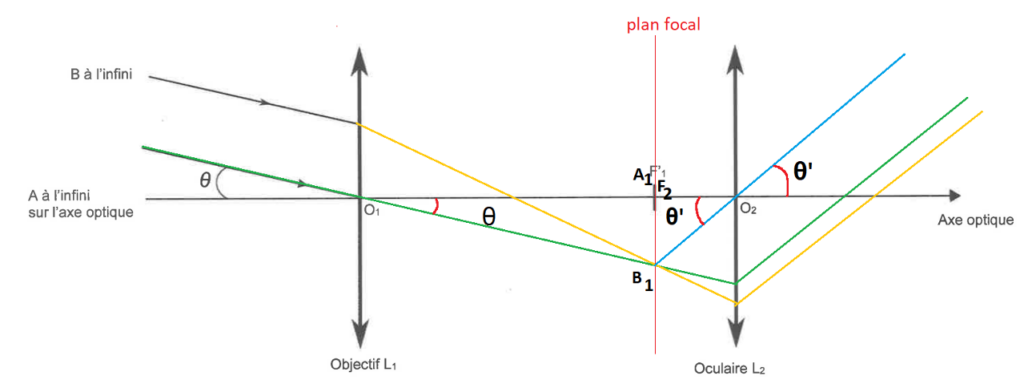
$$
\tan\left(\theta\right)\approx\theta=\frac{A_1B_1}{f_1^\prime}
$$
$$
\tan\left(\theta^\prime\right)\approx\theta^\prime=\frac{A_1B_1}{f_2^\prime}
$$
$$
G_{Huy}=\frac{\theta^\prime}{\theta}=\frac{\frac{A_1B_1}{f_2^\prime}}{\frac{A_1B_1}{f_1^\prime}}=\frac{A_1B_1}{f_2^\prime}\times\frac{f_1^\prime}{A_1B_1}=\frac{f_1^\prime}{f_2^\prime}
$$

Q8. Calculer la valeur du grossissement G_Huy de la lunette utilisée par Huygens.

$$
G_{Huy}=\frac{f_1^\prime}{f_2^\prime}
$$
$$
G_{Huy}=\frac{329}{7,0}=47
$$

Q9. Conclure sur la possibilité pour Huygens de distinguer la surface de Saturne de son premier anneau en utilisant la lunette. La distance entre la surface de Saturne et son premier anneau est égale à D_A-B = 3,17×10⁴ km (figure 5).

$$
\tan\left(\theta\right)\approx\theta=\frac{D_{A-B}}{D_{TS}}
$$
$$
\theta=\frac{D_{A-B}}{D_{TS}}=\frac{3,17\times{10}^4}{1,42\times{10}^9}
$$
$$
\theta=2,23\times{10}^{-5}\ rad
$$

Or
$$
G_{Huy}=\frac{\theta^\prime}{\theta}
$$
$$
\frac{\theta^\prime}{\theta}=G_{Huy}
$$
$$
\theta^\prime=\theta\times G_{Huy}
$$
$$
\theta^\prime=2,23\times{10}^{-5}\times47
$$
$$
\theta^\prime=1,1\times{10}^{-3}\ rad
$$
$\theta^\prime>3,0\times{10}^{-4}\ rad$ : Huygens peut donc distinguer la surface de Saturne de son premier anneau en utilisant la lunette.

2.   Prise en compte de la diffraction dans l’observation astronomique

L’observation des détails d’un objet avec une lunette astronomique est principalement limitée par le phénomène de diffraction. En effet, l’image donnée par l’objectif d’une source ponctuelle « à l’infini » n’est pas un point mais une figure de diffraction circulaire, appelée tache d’Airy, représentée en figure 6.

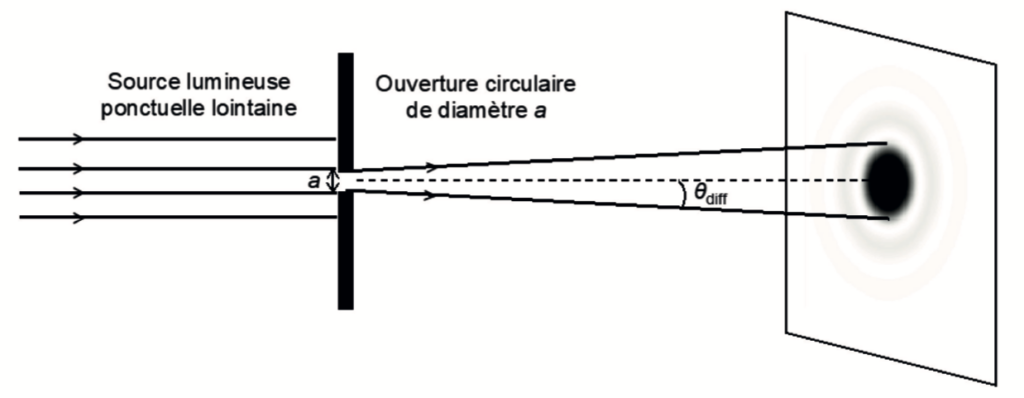
Figure 6. Figure de diffraction obtenue par une ouverture circulaire (échelle non respectée – image en négatif)

Dans le cas de la lunette astronomique, on admet que l’angle caractéristique de diffraction vérifie la relation :

$$\theta_{\mathrm{diff}} = 1,22 \times \frac{\lambda}{a}$$

avec λ la longueur d’onde du faisceau incident et a le diamètre de l’objectif.

Une lunette astronomique ne permet de distinguer deux points A et B que si l’écart angulaire θ entre les directions de ces deux points vus depuis la Terre est supérieur ou égal à l’angle caractéristique de diffraction, c’est-à-dire si la condition θ ≥ θ_diff est vérifiée. Si ce n’est pas le cas, les taches d’Airy associées aux deux points se superposent et les deux points ne peuvent être séparés visuellement.

Q10. Expliquer pourquoi on peut considérer que le phénomène de diffraction a empêché Galilée d’observer les anneaux de Saturne avec sa lunette astronomique contrairement à Huygens qui a pu les observer. Une approche quantitative est attendue.

On rappelle que la distance entre Saturne et la limite du premier anneau visible à l’époque est égale à D_A-B = 3,17×10⁴ km et on effectuera les calculs avec une valeur de la longueur d’onde λ = 550 nm, pour laquelle l’œil humain est le plus sensible.

Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et doit être correctement présentée.

D’après l’énoncé : « Une lunette astronomique ne permet de distinguer deux points A et B que si l’écart angulaire $\theta$ entre les directions de ces deux points vus depuis la Terre est supérieur ou égal à l’angle caractéristique de diffraction, c’est-à-dire si la condition $\theta \geq \theta_{diff}$ est vérifiée. »

Calculons $\theta_{diff}$ pour la lunette de Galilée et pour la lunette de Huygens :
$$
\theta_{diff}=1,22\times\frac{\lambda}{a}
$$
Pour la lunette de Galilée
$$
\theta_{diff,\ gal}=1,22\times\frac{\lambda}{a}
$$
$$
\theta_{diff,\ gal}=1,22\times\frac{550\times{10}^{-9}}{29,0\times{10}^{-3}}
$$
$$
\theta_{diff,\ gal}=2,31\times{10}^{-5}\ rad
$$
$\theta=2,23\times{10}^{-5}\ rad<\theta_{diff,\ gal}$ : le phénomène de diffraction a empêché Galilée d’observer les anneaux de Saturne.

Pour la lunette de Huygens
$$
\theta_{diff,\ Huy}=1,22\times\frac{\lambda}{a}
$$
$$
\theta_{diff,\ Huy}=1,22\times\frac{550\times{10}^{-9}}{51,0\times{10}^{-3}}
$$
$$
\theta_{diff,\ Huy}=1,32\times{10}^{-5}\ rad
$$
$\theta=2,23\times{10}^{-5}\ rad>\theta_{diff,\ Huy}$ : le phénomène de diffraction n’a pas empêché Huygens d’observer les anneaux de Saturne.

3.   Découverte de Titan par Huygens

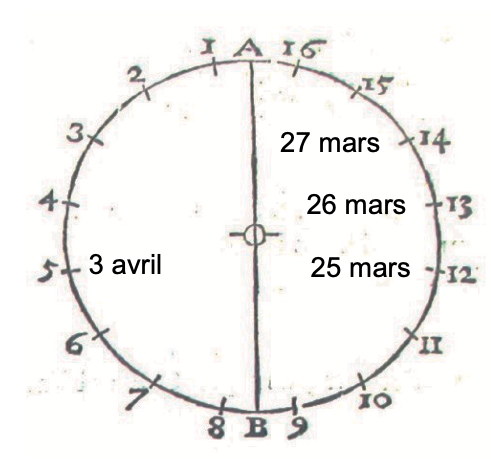
Source : d’après Systema Saturnium, Huygens

Cherchant ensuite sur cette circonférence l’endroit où le satellite s’était trouvé dans notre première observation et corrigeant plusieurs fois cet endroit, […] il m’a semblé enfin que tout le mouvement peut être représenté le plus commodément, si dans le cas de la première observation, celle du 25 mars 1655, le satellite est placé auprès du nombre 12. Par suite le satellite de Saturne était le 26 mars auprès du nombre 13, le 27 mars auprès du nombre 14, le 3 avril auprès du nombre 5 et ainsi de suite aux endroits de l’orbite qui correspondent assez bien avec les situations observées la première année. »

Q11. Justifier le choix de Huygens de diviser la trajectoire de Titan en 16 parties.

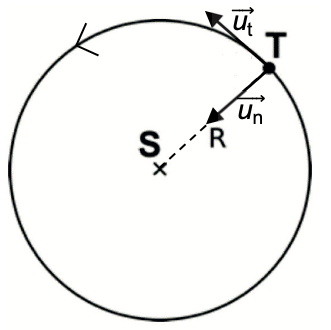
Figure 7. Schéma de la trajectoire de Titan dans le référentiel saturnocentrique

Huygens divise la trajectoire de Titan en 16 pour pouvoir en donner une position précise.

« Après le 25 mars 1655, à savoir le 10 avril, le satellite a été vu à la même position qu’il occupait à cette première date » : du 25 mars au 10 avril il y a 16 jours

« De même, le 3 et le 19 avril de cette même année des positions identiques furent observées » : du 3 au 19 avril il y a 16 jours

« de même encore le 13 et le 29 de ce mois » : du 13 au 29 il y a 16 jours.

Tout les 16 jours la position occupée est identique. Ainsi, Huygens divise la trajectoire de Titan en 16 pour pouvoir faire une mesure par jour et qu’au bout de 16 jours (sa période) le cycle recommence.

Q12. Donner     l’expression     vectorielle     de     la     force     d’interaction gravitationnelle exercée par Saturne sur le satellite Titan en fonction de G, M_S, M_T, R et de l’un des vecteurs unitaires.

$$
\overrightarrow{F_{S/T}}=G\times\frac{M_S\times M_T}{R^2}\overrightarrow{u}_N
$$

Q13. Le mouvement de Titan autour de S est supposé circulaire. Montrer qu’il est uniforme puis que l’expression de la vitesse du satellite s’écrit sous la forme :

$$v=\sqrt{\frac{G\cdot M_S}{R}}$$

Système : Titan
Référentiel : saturnocentrique supposé galiléen.

D’après la 2nd loi de Newton :
$$
\Sigma\overrightarrow{F_{ext}}=M_T\overrightarrow{a}
$$
$$
\overrightarrow{F_{S/T}}=M_T\overrightarrow{a}
$$
$$
G\times\frac{M_S\times M_T}{R^2}\overrightarrow{u}_N=M_T\overrightarrow{a}
$$
$$
\overrightarrow{a}=G\times\frac{M_S}{R^2}\overrightarrow{u}_N
$$

Pour un mouvement circulaire, dans le repère de Frenet, le vecteur accélération est de la forme :
$$
\overrightarrow{a}=\frac{v^2}{R}\overrightarrow{u}_N+\frac{dv}{dt}\overrightarrow{u}_T
$$

L’accélération étant unique, par identification :
$\frac{dv}{dt}=0$ donc la vitesse est constante : le mouvement est uniforme
$$
\frac{v^2}{R}=G\times\frac{M_S}{R^2}
$$
$$
v^2=G\times\frac{M_S}{R}
$$
$$
v=\sqrt{G\times\frac{M_S}{R}}
$$
$$
v=\sqrt{\frac{G\times M_S}{R}}
$$

Q14. En déduire l’expression de la période de révolution notée T_Kep de Titan. Calculer sa valeur. Commenter.

La période de révolution est :
$$
T=\frac{\text{Périmètre d’un cercle}}{\text{vitesse}}=2\pi R v=2\pi R\sqrt{\frac{G\times M_S}{R}}
$$
$$
T=2\pi\sqrt{R^2\frac{R}{G\times M_S}}
$$
$$
T=2\pi\sqrt{\frac{R^3}{G\times M_S}}
$$
$$
T_{Kep}=2\pi\sqrt{\frac{\left(1,22\times{10}^6\times{10}^3\right)^3}{6,67\times{10}^{-11}\times5,68\times{10}^{26}}}
$$
$$
T_{Kep}=1,38\times{10}^6 s
$$
$$
T_{Kep}=15\ jours\ 23\ heures\ 20\ min
$$

$$
T_{Huy}=15\ jours\ 23\ heures\ 13\ min
$$
$T_{Kep}$ et $T_{Huy}$ sont identiques.

ANNEXE À RENDRE AVEC LA COPIE