à la découverte des lunes glacées de Jupiter

Bac Liban 2024 Sujet 2

Exercice 2 – (6 points) –  Durée 1h03 – Calculatrice autorisée

Sujet n°24-PYCJ2G11

EXERCICE 2 : à la découverte des lunes glacées de Jupiter (6 points)

Exploring Jupiter and Ganymede (artist’s impression). Source : esa.int

Le but de cet exercice est d’étudier le mouvement de la sonde JUICE autour de Ganymède.

Données :

• rayon de Ganymède : R_G = 2,63×10³ km ;
• masse de Ganymède : M_G = 1,82×10²³ kg ;
• distance maximale entre Jupiter et la Terre : 9,3×10⁸ km ;
• valeur de la constante gravitationnelle : G = 6,67×10^-11 m³·kg^–1·s^–2 ;
• la valeur de la vitesse de la lumière dans le vide est supposée connue.

1.    Orbites de la sonde JUICE autour de Ganymède

À partir de décembre 2034, la sonde JUICE se placera sur différentes orbites autour de Ganymède :

• durant une première phase de 30 jours, la sonde circulera sur une orbite elliptique ;
• elle restera ensuite 90 jours sur une orbite circulaire d’altitude 5 000 km ;
• une nouvelle manœuvre la placera sur une orbite circulaire d’altitude 500 km d’où elle étudiera Ganymède durant 102 jours ;
• enfin, la sonde se placera sur une orbite circulaire d’altitude inférieure à 500 km pour une durée de 30 jours.

Source : Wikipedia

On s’intéresse à l’orbite circulaire d’altitude h = 500 km de la sonde JUICE autour de Ganymède.

Q.1. Schématiser, sans souci d’échelle, Ganymède et l’orbite de la sonde JUICE. Placer le repère de Frenet $(\overrightarrow{u_t},\overrightarrow{u_n})$ et représenter $\overrightarrow{F_G}$ la force d’interaction gravitationnelle à laquelle la sonde JUICE est soumise de la part de Ganymède, à un point quelconque de sa trajectoire.

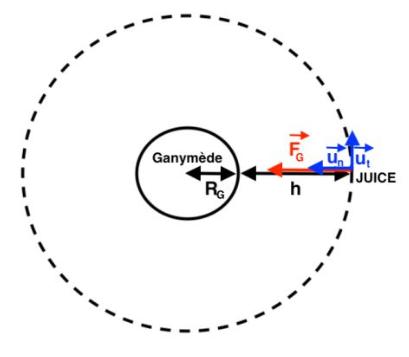
Q.2.  Exprimer, dans le repère de Frenet, le vecteur de la force $\overrightarrow{F_G}$ .

$$\vec{F_G}=\vec{F_{Ganymede/JUICE}}=G\times\frac{M_G\times M_J}{\left(R_G+h\right)^2}{\vec{u}}_N$$

Q.3.  On considère que $\overrightarrow{F_G}$ est la seule force qui s’exerce sur la sonde JUICE. Montrer que la sonde JUICE a un mouvement circulaire uniforme dans le référentiel, supposé galiléen, centré sur Ganymède.

Système : sonde JUICE
Référentiel : Centré sur Ganymède supposé galiléen.

D’après la 2^nd loi de Newton :

$$\Sigma\vec{F_{ext}}=M_J\vec{a}$$

$$\vec{F_{Ganymede/JUICE}}=M_J\vec{a}$$

$$G\times\frac{M_G\times M_J}{\left(R_G+h\right)^2}{\vec{u}}_N=M_J\vec{a}$$

$$\vec{a}=G\times\frac{M_G}{\left(R_G+h\right)^2}{\vec{u}}_N$$
Pour un mouvement circulaire, dans le repère de Frenet, le vecteur accélération est de la forme :
$$\vec{a}=\frac{v^2}{R_G+h}{\vec{u}}_N+\frac{dv}{dt}{\vec{u}}_T$$

L’accélération étant unique, par identification :
$$\frac{dv}{dt}=0$$ donc la vitesse est constante : le mouvement est uniforme.

Q.4.  Montrer que la vitesse de la sonde JUICE peut s’écrire :

$$v=\sqrt{\frac{G\times M_G}{R_G+h}}$$

$$\vec{a}=G\times\frac{M_G}{\left(R_G+h\right)^2}{\vec{u}}_N$$
Pour un mouvement circulaire, dans le repère de Frenet, le vecteur accélération est de la forme :
$$\vec{a}=\frac{v^2}{R_G+h}{\vec{u}}_N+\frac{dv}{dt}{\vec{u}}_T$$

L’accélération étant unique, par identification :
$$\frac{v^2}{R_G+h}=G\times\frac{M_G}{\left(R_G+h\right)^2}$$

$$v^2=G\times\frac{M_G}{R_G+h}$$
$$v=\sqrt{G\times\frac{M_G}{R_G+h}}$$
$$v=\sqrt{\frac{G\times M_G}{R_G+h}}$$

Q.5.  Établir l’expression de la période T en fonction de R_G, h, M_G et G puis en déduire que sur l’orbite circulaire d’altitude 500 km, la sonde JUICE a une période de valeur proche de T₅₀₀ = 2,77 h.

La période de révolution est :
T=Périmètre d’un cercle / vitesse
$$T=2\pi\times\frac{R_G+h}{v}$$
$$T=2\pi\times\frac{R_G+h}{\sqrt{\frac{G\times M_G}{R_G+h}}}$$
$$T=2\pi\times\sqrt{\left(R_G+h\right)^2\times\frac{R_G+h}{G\times M_G}}$$
$$T=2\pi\sqrt{\frac{\left(R_G+h\right)^3}{G\times M_G}}$$

$$T_{500}=2\pi\sqrt{\frac{\left(2,63\times{10}^3\times{10}^3+500\times{10}^3\right)^3}{6,67\times10^{-11}\times1,82\times{10}^{23}}}$$
$$T_{500}=9,99{\times10}^3\ s$$
$$T_{500}=\frac{9,99{\times10}^3}{3600}$$
$$T_{500}=2,77\ h$$

Q.6.  En utilisant la troisième loi de Kepler, déterminer la période de la sonde JUICE sur son orbite circulaire d’altitude 5 000 km.

D’après la 3^ème loi de Kepler :
$$\frac{T^2}{r^3}=Constante$$

Ainsi :
$$\frac{T_{circulaire}^2}{\left(R_G+h_{circulaire}\right)^3}=\frac{T_{500}^2}{\left(R_G+h_{500}\right)^3}$$
$$T_{circulaire}^2=\frac{T_{500}^2}{\left(R_G+h_{500}\right)^3}\times\left(R_G+h_{circulaire}\right)^3$$
$$T_{circulaire}=\sqrt{\frac{T_{500}^2}{\left(R_G+h_{500}\right)^3}\times\left(R_G+h_{circulaire}\right)^3}$$

$$T_{circulaire}=\sqrt{\frac{\left(9,99{\times10}^3\right)^2}{\left(2,63\times{10}^3\times{10}^3+500\times{10}^3\right)^3}\times\left(2,63\times{10}^3\times{10}^3+5000\times{10}^3\right)^3}$$
$$T_{circulaire}=3,80{\times10}^4\ s$$

« Les 1167 orbites que la sonde JUICE effectuera autour de Ganymède suffiront à révéler les secrets qu’elle cache sous sa couche de glace. »

D’après Science&Vie du 19 avril 2023.

Q.7.  En utilisant les réponses aux questions 5 et 6, estimer le nombre d’orbites effectuées par la sonde JUICE autour de Ganymède et commenter la phrase ci-dessus.

D’après le texte, la sonde JUICE se placera sur différentes orbites autour de Ganymède :
90 jours sur une orbite circulaire d’altitude 5 000 Km
102 jours sur une orbite circulaire d’altitude 500 Km

Calculons le nombre de tours effectuées durant ces deux phases :

102 jours sur une orbite circulaire d’altitude 500 Km

1 Tour	$9,99{\times10}^3\ s$
N Tours	$102\ jours=102\times24\times3600={8,8\times10}^6\ s$

$$N=\frac{{8,8\times10}^6\times1}{9,99{\times10}^3}$$
$$N=880\ tours$$

90 jours sur une orbite circulaire d’altitude 5 000 Km

1 Tour	$3,80{\times10}^4\ s$
N Tours	$90\ jours=90\times24\times3600={7,8\times10}^6\ s$

$$N=\frac{{7,8\times10}^6\times1}{3,80{\times10}^4}$$
$$N=205\ tours$$

JUICE tournera 880+205=1085 fois autour de Ganymède pendant ces deux phases. Durant les deux autre phases, JUICE effectuera d’autres tours pour atteindre les 1167 tours.

Le candidat est invité à prendre des initiatives et à présenter sa démarche. Toute démarche pertinente, même non aboutie, sera valorisée.

2.    Communication avec la Terre

« Le temps mis par le signal radio pour faire un aller-retour de la sonde JUICE à la Terre est de 1 h 46. »

D’après Wikipedia

Q.8.  Indiquer à quel type d’ondes les ondes radio appartiennent : mécanique ou électromagnétique.

Les ondes radio appartiennent aux ondes électromagnétiques.

Q.9.  Montrer, en négligeant la distance entre la sonde JUICE et Jupiter, que le temps mis par le signal radio pour faire un aller-retour entre la sonde JUICE et la Terre est proche de celui annoncé.

Calculons le temps mis par le signal radio pour faire un aller-retour :
$$c=2\times\frac{d}{\Delta t}$$
$$c\times\Delta t=2\times d$$
$$\Delta t=\frac{2\times d}{c}$$
$$\Delta t=\frac{2\times9,3\times{10}^8\times{10}^3}{3,00\times{10}^8}$$
$$\Delta t=6200\ s$$
$$\Delta t=1h\ 43min\ 20\ s$$

Remarque : ce temps est proche de celui annoncé dans le texte.