Bac Centres étrangers 2023 Sujet 1
Exercice 2 – (5 points) – Durée 0h53 – Calculatrice autorisée
Sujet n°23-PYCJ1G11
Sujet et corrigé
EXERCICE 2 – À LA RECHERCHE D’UNE AUTRE TERRE (6 points)
Les astronomes s’intéressent particulièrement aux exoplanètes (planètes situées en dehors de notre système solaire) présentant des similitudes avec notre Terre car elles pourraient éventuellement réunir des conditions indispensables à l’apparition de la vie telle que nous la connaissons.
L’objectif de cet exercice est de déterminer quelques caractéristiques d’une exoplanète dont la découverte a été annoncée en décembre 2021, dans le cadre d’un projet international.
Cette exoplanète est nommée GJ 367b, elle sera notée P dans cet exercice. Elle est en orbite autour de l’étoile hôte GJ 367, qui sera notée E.
Donnée
Constante de gravitation universelle : G = 6,67×10-11 m3⋅kg-1⋅s-2
Partie A – Détection par la méthode du transit
Une exoplanète peut être détectée par la méthode du transit planétaire qui consiste à mesurer régulièrement la luminosité d’une étoile afin de détecter la baisse périodique de sa luminosité. Cette baisse de luminosité est associée au passage par rapport à l’observateur d’une exoplanète devant l’étoile (figure 1 et figure 2 ci-dessous).
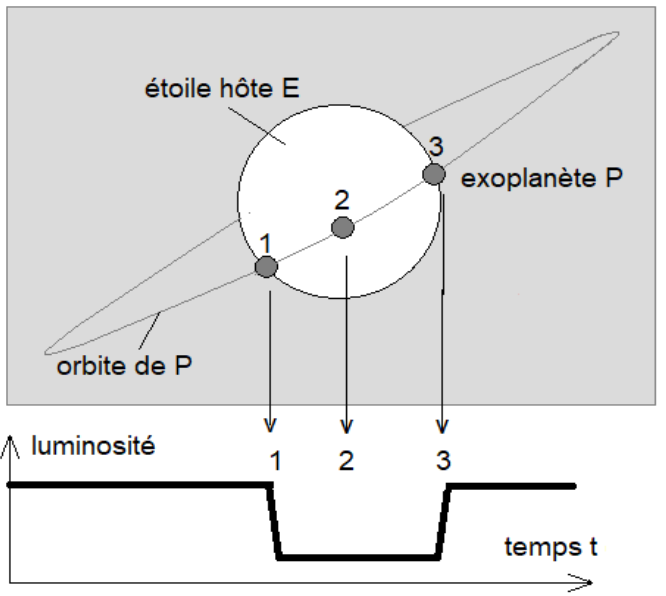
Figure 1. Variation de la luminosité de l’étoile lors d’un transit
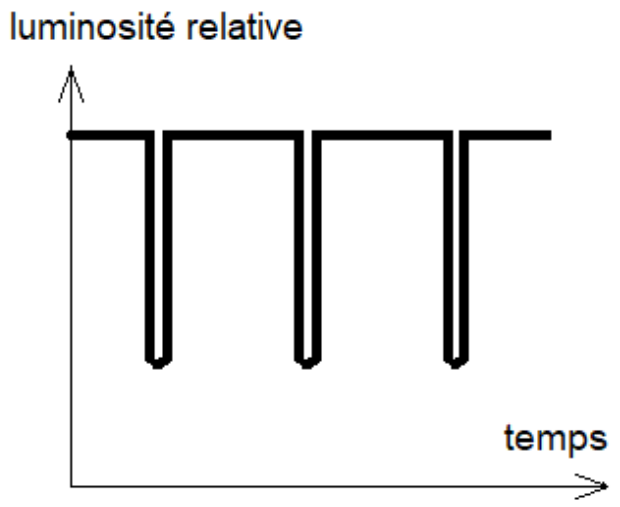
Figure 2. Variation de la luminosité d’une étoile pour trois transits consécutifs
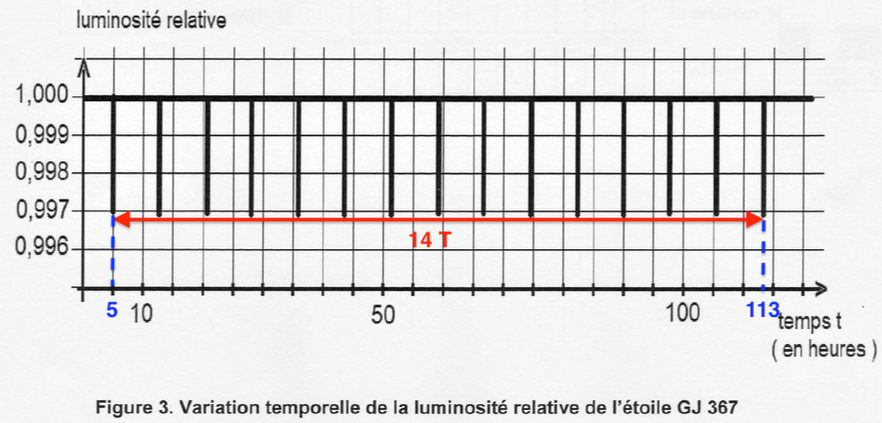
1. À partir de la figure 3 (ANNEXE PAGE 12/12 À RENDRE AVEC LA COPIE), justifier l’utilisation du terme « périodique » pour décrire la variation de luminosité de l’étoile.
La luminosité de l’étoile varie de manière identique à intervalle de temps égaux : elle est périodique.
2. À partir de la figure 3 (ANNEXE PAGE 12/12 À RENDRE AVEC LA COPIE), déterminer la valeur de la période T du phénomène observé le plus précisément possible, en indiquant la méthode employée.
Pour déterminer la valeur de la période le plus précisément possible, on mesure un grand nombre et on en déduit T :
$$14T=113-5$$
$$14T=108$$
$$T=\frac{108}{14}$$
$$T=7,7\ h$$
Partie B – Mouvement de l’exoplanète GJ 367b
Dans le référentiel de l’étoile E, supposé galiléen, on considère que l’orbite de l’exoplanète P est circulaire, de centre O (centre de l’étoile) et de rayon r. La masse de l’exoplanète est notée mP.
Par ailleurs, l’exploitation d’observations complémentaires a permis de déterminer la valeur de la masse de l’étoile E : ME = 9,5×1029 kg.
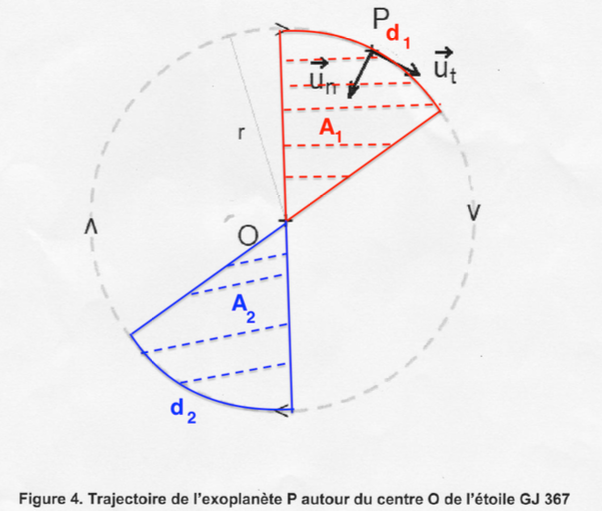
3. Sans souci d’échelle, représenter sur la figure 4 (ANNEXE PAGE 12/12 À RENDRE AVEC LA COPIE) la force gravitationnelle exercée par l’étoile E sur l’exoplanète P.
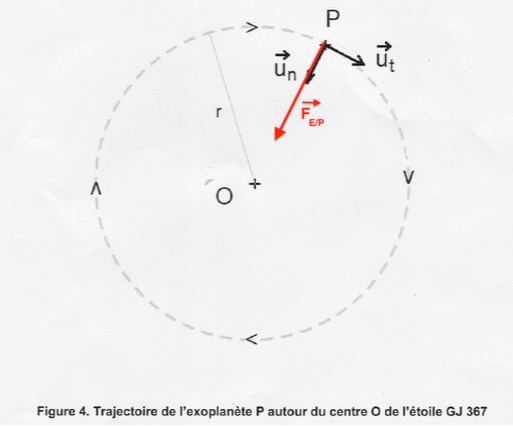
4. Écrire l’expression vectorielle de cette force dans le repère de Frenet $(P,\overrightarrow{u_t},\overrightarrow{u_n})$ en fonction de G, ME, mP et r.
$${\overrightarrow{F}}_{E/P}=G\times\frac{M_E\times m_P}{r^2}{\overrightarrow{u}}_N$$
5. Énoncer la deuxième loi de Kepler, dite « loi des aires ».
2eme loi de Kepler : Loi des aires Le segment soleil planète balaie des aires égales au cours de durées égales.
6. Compléter la figure 4 (ANNEXE PAGE 12/12 À RENDRE AVEC LA COPIE) afin d’illustrer cette loi et justifier que le mouvement de l’exoplanète P est uniforme.
2eme loi de Kepler : $A_1=A_2$
or le mouvement est circulaire, ainsi $d_1=d_2$
Or les durées sont égales $\Delta t1=\Delta t2=\Delta t$
D’ou
$$\frac{d_1}{\Delta t}=\frac{d_2}{\Delta t}$$
$$v_1=v_2$$
Le mouvement de l’exoplanète P est uniforme.
7. Appliquer la deuxième loi de Newton à l’exoplanète P et démontrer que la vitesse vP de l’exoplanète P sur son orbite peut s’écrire : $v_P=\sqrt{\frac{G\times M_E}{r}} $ .
Système : exoplanète P
Référentiel : Centre de E supposé galiléen
D’après la 2nd loi de Newton :
$$\Sigma \overrightarrow{F_{ext}}=m_p\overrightarrow{a}$$
$${\overrightarrow{F}}_{E/P}=m_p\overrightarrow{a}$$
$$G\times\frac{M_E\times m_P}{r^2}{\overrightarrow{u}}_N=m_p\overrightarrow{a}$$
$$\overrightarrow{a}=G\times\frac{M_E}{r^2}{\overrightarrow{u}}_N$$
Pour un mouvement circulaire, dans le repère de Frenet, le vecteur accélération est de la forme:
$$\overrightarrow{a}=\frac{v_p^2}{r}{\overrightarrow{u}}_N+\frac{dv}{dt}{\overrightarrow{u}}_t$$
L’accélération étant unique, par identification :
$$\frac{v_p^2}{r}=G\times\frac{M_E}{r^2}$$
$$v_p^2=G\times\frac{M_E}{r}$$
$$v_p=\sqrt{G\times\frac{M_E}{r}}$$
8. Donner l’expression de la période de révolution T de l’exoplanète P en fonction de sa vitesse vP et du rayon r de son orbite circulaire. En déduire l’égalité suivante :
$T^2=\frac{4\pi^2\times r^3}{G\times M_E}$.
$$v_p=\frac{2\pi r}{T}$$
$$T=\frac{2\pi r}{v_p}$$
$$T^2=\frac{4\pi^2r^2}{v_p^2}$$
Or
$$v_p^2=G\times\frac{M_E}{r}$$
D’ou
$$T^2=\frac{4\pi^2r^2}{G\times\frac{M_E}{r}}$$
$$T^2=\frac{4\pi^2r^2}{G\times M_E}\times r$$
$$T^2=\frac{4\pi^2r^3}{G\times M_E}$$
9. En admettant que T = 7,7 h, montrer que la valeur du rayon r de la trajectoire circulaire de l’exoplanète autour de l’étoile E est proche d’un million de kilomètres.
$$T^2=\frac{4\pi^2r^3}{G\times M_E}$$
$$\frac{4\pi^2r^3}{G\times M_E}=T^2$$
$$r^3=\frac{T^2\times G\times M_E}{4\pi^2}$$
$$r=\sqrt[3]{\frac{T^2\times G\times M_E}{4\pi^2}}$$
Ou
$$r=\left(\frac{T^2\times G\times M_E}{4\pi^2}\right)^\frac{1}{3}$$
$$r=\left(\frac{\left(7,7\times 60\times 60\right)^2\times 6,67\times {10}^{-11}\times 9,5\times {10}^{29}}{4\pi^2}\right)^\frac{1}{3}$$
$$r=1,1\times {10}^9\ m$$
$$r=1,1\times {10}^6\ km$$
$$r=1,1\ million\ de\ km$$
La valeur du rayon r de la trajectoire circulaire de l’exoplanète autour de l’étoile E est proche d’un million de kilomètres.
Partie C – GJ 367b : une exoplanète de fer ?
Concernant l’exoplanète GJ 367b, en décembre 2021, un magazine scientifique titre « Une planète de fer a été découverte ».
Les chercheurs ont pu déterminer que l’exoplanète P a un volume VP égal à 37 % du volume de la Terre VT et une masse MP égale à 55 % de la masse de la Terre MT.
Données
- Masse de la Terre : MT = 5,97×1024 kg
- Rayon de la Terre : RT = 6,37×106 m
- Masse volumique du fer : ρ(Fe) = 7,9×103 kg·m-3
- Volume d’une sphère de rayon r : $V=\frac{4}{3}\pi\times r^3$
10. Calculer la masse volumique de la planète et justifier la référence au fer dans le titre « Une planète de fer a été découverte ».
$$\rho_p=\frac{M_p}{V_p}$$
Or d’apres l’énnoncé :
$M_p=55%M_T$
$V_p=37%V_T$
$$\rho_p=\frac{55%M_T}{37%V_T}$$
Or
$$V_T=\frac{4}{3}\pi\times R_T^3$$
$$\rho_p=\frac{55%M_T}{37%\frac{4}{3}\pi\times R_T^3}$$
$$\rho_p=\frac{\frac{55}{100}\times 5,97\times {10}^{24}}{\frac{37}{100}\times \frac{4}{3}\pi\times \left(6,37\times {10}^6\right)^3}$$
$$\rho_p=8,20\times {10}^3\ kg.m^{-3}$$
$\rho_p$ est du même ordre de grandeur que $\rho\left(Fe\right)=7,9\times {10}^3\ kg.m^{-3}$ d’ou le titre « une planète de fer a été découverte »
ANNEXE A RENDRE AVEC LA COPIE
EXERCICE 2
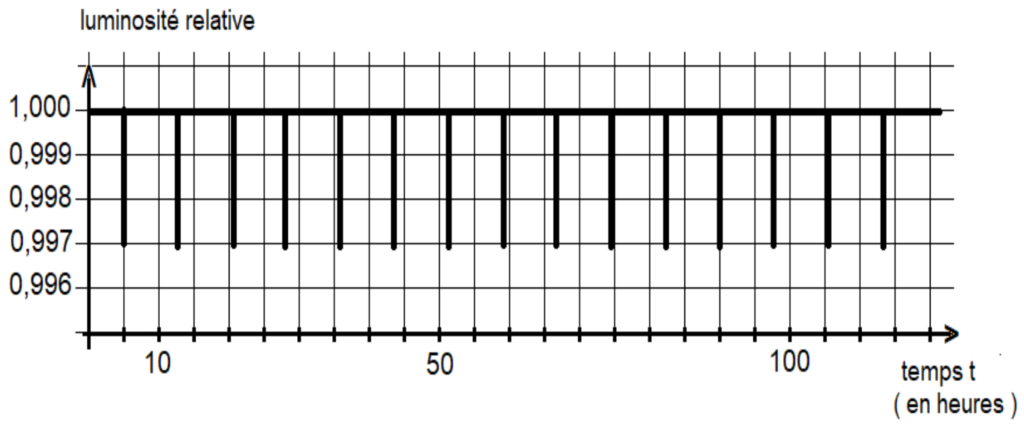
Figure 3. Variation temporelle de la luminosité relative de l’étoile GJ 367
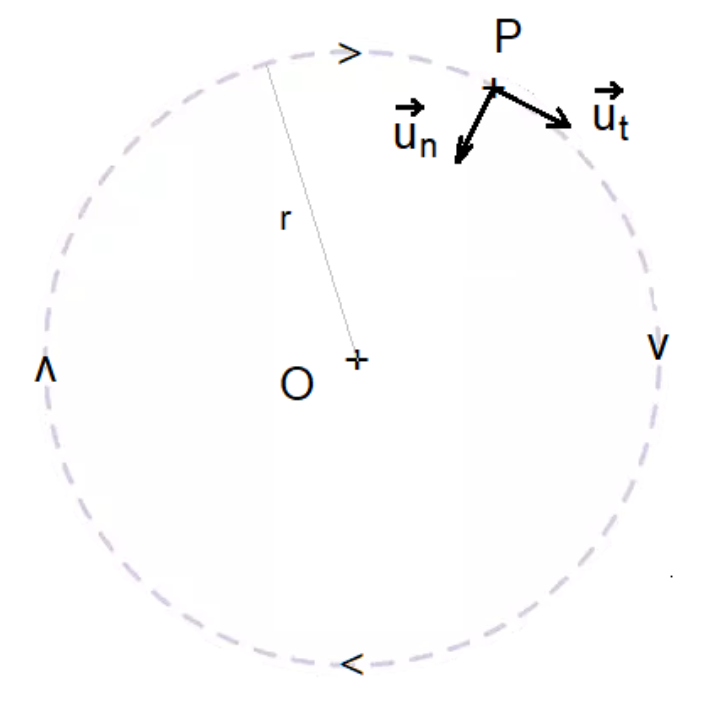
Figure 4. Trajectoire de l’exoplanète P autour du centre O de l’étoile GJ 367
