Accéléromètre d’un mobile multifonction

Bac Métropole 2024 Sujet 1

Exercice 3 – (6 points) –  Durée 1h03 – Calculatrice autorisée

Sujet n°24-PYCJ1ME1

Sujet et corrigé

Exercice 3 – Accéléromètre d’un mobile multifonction (6 points)

Données :

• masse du smartphone utilisé : m = 182 g ;
• intensité de la pesanteur terrestre : g = 9,81 m·s^–2 ;
• dans tout l’exercice, on ne tient pas compte de la poussée d’Archimède exercée par l’air sur le smartphone.

Le mouvement du centre de masse G du smartphone est étudié dans le référentiel terrestre supposé galiléen, muni d’un repère d’espace d’axe (Oz), vertical, orienté vers le haut et de vecteur unitaire $\overrightarrow{k}$ (voir figure 1). À la date t = 0, le smartphone est lâché à plat, avec une vitesse initiale nulle. Son centre de masse G se trouve alors au point H de coordonnée z = h. Il est réceptionné quelques instants plus tard sur un coussin posé au sol. Lorsque le smartphone est en contact avec le coussin, son centre de masse est à l’altitude z = 0.

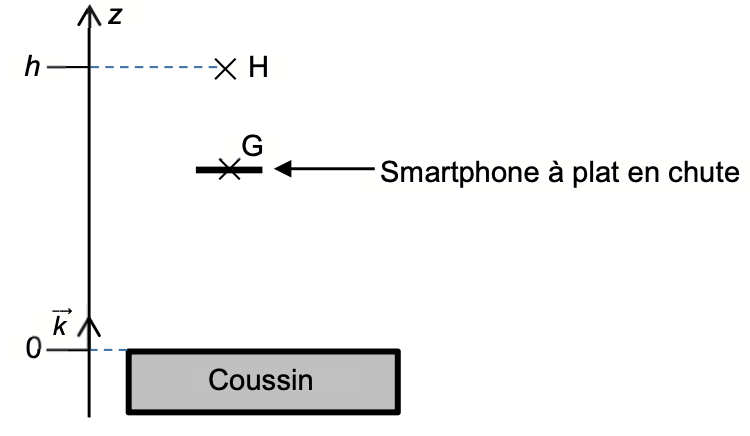
Figure 1. Modélisation de la chute du smartphone

1.   Modèle de la chute libre sans frottement

On fait tout d’abord l’hypothèse que le smartphone est en mouvement de chute libre verticale. On ne tient donc pas compte des forces de frottement exercées par l’air sur le smartphone en mouvement.

Q1. Dans ce modèle, faire un bilan des forces appliquées au système {smartphone}. En déduire l’expression de la coordonnée a_z de l’accélération du centre de masse G du système.

En chute libre, le système (smartphone) n’est soumis qu’a son poids.

Système {smartphone}
Référentiel terrestre supposé galiléen

D’après la deuxième loi de newton :
$\Sigma\overrightarrow{F_{ext}}=m\overrightarrow{a}$
$\overrightarrow{P}=m\overrightarrow{a}$
$m\overrightarrow{g}=m\overrightarrow{a}$
$\overrightarrow{g}=\overrightarrow{a}$

Or
$$\overrightarrow{g}\begin{pmatrix}0 \\ -g\end{pmatrix}$$

Le vecteur accélération du centre d’inertie du solide est égal au vecteur champ de pesanteur.

$$\overrightarrow{a}\begin{pmatrix}a_x=0 \\ a_z=-g\end{pmatrix}$$

Ainsi : $a_z=-g$

Q2. Établir l’expression de la coordonnée vz(t) de la vitesse du centre de masse G du système puis montrer que l’équation horaire de l’altitude z(t) du centre de masse G a pour expression :

$$ z(t)=-\frac{1}{2}\cdot g\cdot t^2+h $$

$a_z=\frac{dv_{z\left(t\right)}}{dt}$
On intègre l’accélération :
$v_{z\left(t\right)}=-gt+C_1$

Pour trouver les constantes, on utilise la vitesse initiale. Or, d’après le sujet, le smartphone est lâché avec une vitesse initiale nulle : $v_{0z}=0$
d’ou
$v_{z\left(t\right)}=-gt$
$v_{z\left(t\right)}=\frac{dz\left(t\right)}{dt}$
On intègre la vitesse :
$z\left(t\right)=-\frac{1}{2}gt^2+C_2$
Pour trouver les constantes, on utilise $z_0=h$
d’ou
$z\left(t\right)=-\frac{1}{2}gt^2+h$

On choisit l’origine de l’énergie potentielle de pesanteur E_PP(z) au niveau de l’origine de l’axe (Oz) : E_PP(z = 0) = 0.

Q3. Justifier que l’énergie mécanique E_M du smartphone est constante et qu’elle a pour expression : E_M = m·g·h.

$E_m=E_c+E_{pp}$
$E_m=\frac{1}{2}\times m\times v^2+m\times g\times z$
Or, en l’absence de frottements, l’énergie mécanique se conserve :
$E_m=E_m\left(0\right)=\frac{1}{2}\times m\times v_0^2+m\times g\times h$
Or $v_0=0$
Ainsi :
$E_m=m\times g\times h$

2.   Étude expérimentale de la chute du smartphone

Pour confronter le modèle de chute libre sans frottement à l’expérience, on lâche à la date t = 0 un téléphone équipé d’un accéléromètre, avec une vitesse initiale nulle depuis la hauteur h = 1,70 m. La figure 2 est obtenue à partir des valeurs de l’accélération enregistrées par le capteur entre le lâcher du téléphone et la date t = 0,47 s.

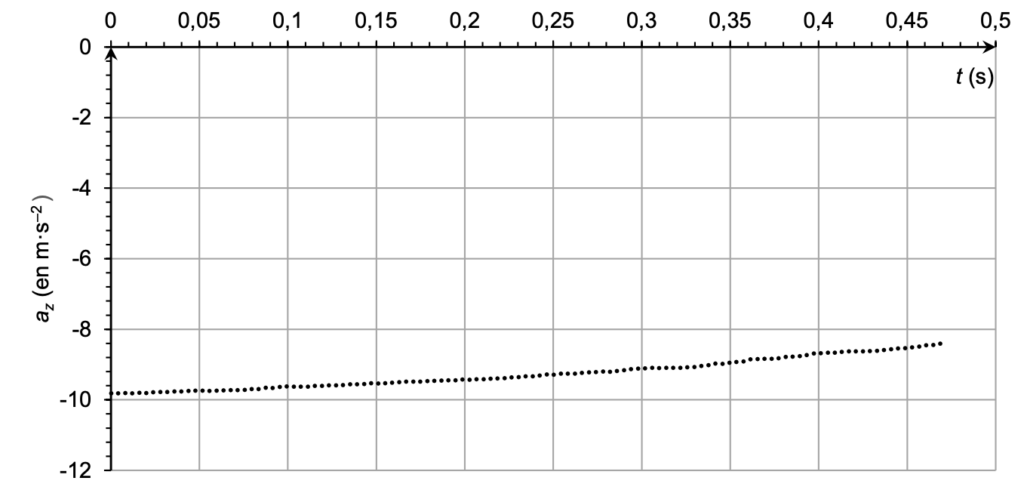
Figure 2. Accélération verticale a_z du smartphone en fonction du temps t

Q4. Indiquer, en justifiant, si l’évolution temporelle de la valeur de la composante a_z de l’accélération obtenue expérimentalement est compatible avec le modèle de chute libre sans frottement.

D’après la figure 2, $a_z$ n’est pas constant au cours du temps.
Le modèle de la chute libre sans frottement donne $a_z=g=\text{constante}$.
Ainsi, l’évolution temporelle de la valeur de la composante $a_z$ de l’accélération obtenue expérimentalement n’est pas compatible avec le modèle de la chute libre (sans frottement).

Le traitement des données acquises permet de tracer l’évolution temporelle de trois formes d’énergies du smartphone : énergie potentielle de pesanteur EPP(t), énergie cinétique EC(t) et énergie mécanique EM(t), comme représenté sur la figure 3.

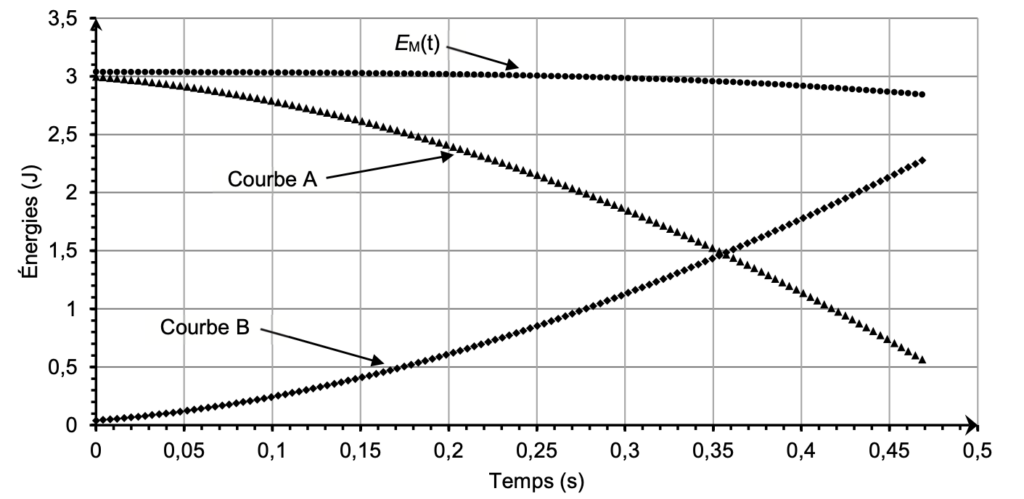
Figure 3. Représentations graphiques de E_PP(t), E_C(t) et E_M(t) lors de la chute du smartphone

Q5. Associer, en justifiant, chaque courbe d’évolution temporelle A et B de la figure 3 à la forme d’énergie correspondante.

$E_{pp}=m\times g\times z$ : l’énergie potentielle de pesanteur est proportionnelle à l’altitude. Lors de la chute, $z$ diminue donc $E_{pp}$ diminue : Courbe A

$E_c=\frac{1}{2}\times m\times v^2$ : à l’instant initiale, la vitesse étant nulle, l’énergie cinétique est nulle. La vitesse augmente au cours du temps, l’énergie cinétique augmente au cours du temps : courbe B

Q6. Montrer, à partir de la figure 3, que la vitesse du smartphone est proche de 5 m·s^–1 à la date t = 0,45 s.

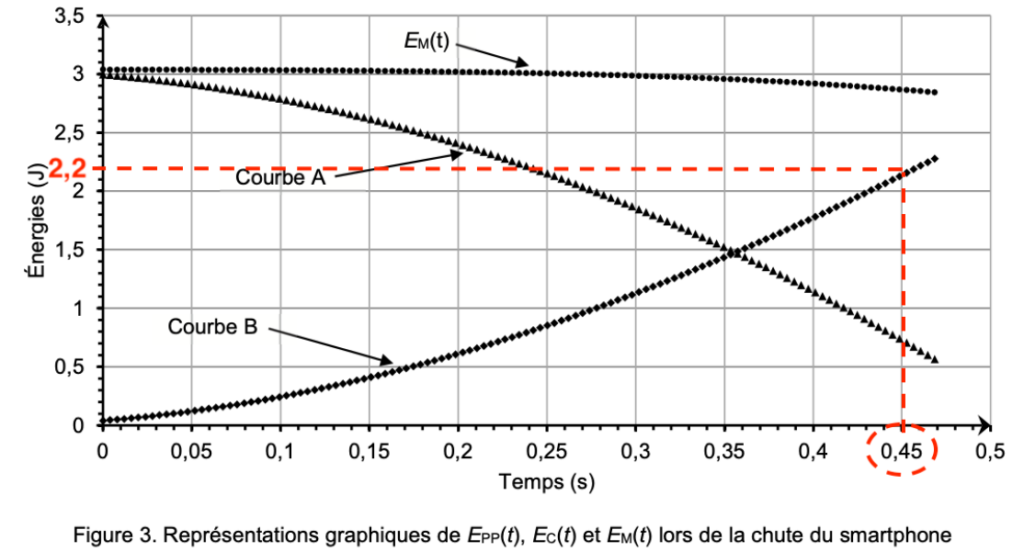
Pour $t=0,45\ s$, $E_c=2,2\ J$
$E_c=\frac{1}{2}\times m\times v^2$
$\frac{1}{2}\times m\times v^2=E_c$
$v^2=\frac{2\times E_c}{m}$
$v=\sqrt{\frac{2\times E_c}{m}}$
$v=\sqrt{\frac{2\times2,2}{182\times{10}^{-3}}}$
$v=4,9\ m.s^{-1}$

Ainsi, la vitesse du smartphone est proche de $5\ m.s^{-1}$ à la date $t=0,45\ s$.

Les actions de frottement de l’air sur le smartphone sont représentées par une force $\overrightarrow{f}$ verticale et dirigée vers le haut. Cette force est nulle lorsque la vitesse du smartphone est nulle.

Q7. En appliquant la deuxième loi de Newton au système {smartphone}, montrer que la coordonnée verticale de la force de frottement vérifie :

f = m·(a_z+ g)

Système {smartphone}
Référentiel terrestre supposé galiléen

D’après la deuxième loi de newton :
$\Sigma\overrightarrow{F_{ext}}=m\overrightarrow{a}$
$\overrightarrow{P}+\overrightarrow{f}=m\overrightarrow{a}$
$m\overrightarrow{g}+\overrightarrow{f}=m\overrightarrow{a}$
Projetons sur l’axe Oz :
$-mg+f=ma_z$
$f=ma_z+mg$
$f=m\times\left(a_z+g\right)$

Les données expérimentales permettent de représenter les variations de la composante verticale de l’accélération az du smartphone en fonction du carré v² de sa vitesse. Les résultats sont représentés sur la figure 4. Les données expérimentales sont correctement représentées par une modélisation affine :

a_z = 0,0555 × v ² – 9,80             où a_z est exprimée en m·s^–2 et v en m·s^–1

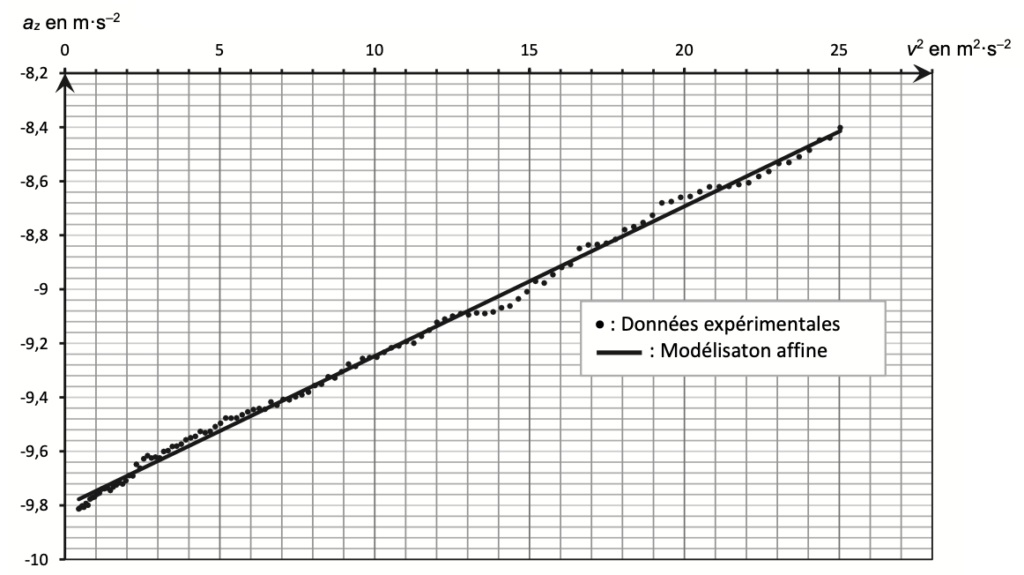
Figure 4. Modélisation de la représentation de a_z en fonction de v²

Q8. Déterminer la valeur expérimentale de l’intensité de la pesanteur g que l’on peut déduire de cette expérience.

$a_z=0,0555\times v^2-9,80$

L’intensité de pesanteur $g$ est obtenue lorsque qu’il n’y a pas de frottements, lorsque la vitesse du smartphone est nulle :
$g=0,0555\times0^2-9,80$
$g=9,80\ m.s^{-2}$

Q9. Montrer que l’on peut déduire de ces résultats que la force de frottement exercée par l’air peut s’écrire f = k · v² où k est un coefficient dont on donnera la valeur et l’unité.

D’après la relation de Q7 :
$f=m\times\left(a_z+g\right)$
$m\times\left(a_z+g\right)=f$
$a_z+g=\frac{f}{m}$
$a_z=\frac{f}{m}-g$

D’après la modélisation :
$a_z=0,0555\times v^2-9,80$

Par identification :
$\frac{f}{m}=0,0555\times v^2$
$f=0,0555\times v^2\times m$
$f=0,0555\times m\times v^2$

Ainsi :
$f=k\times v^2$
Avec $k=0,0555\times m$

Unité de $k$ :
$f=k\times v^2$
$k=\frac{f}{v^2}$
$\left[k\right]=\frac{\left[f\right]}{\left[v\right]^2}$
$\left[k\right]=\frac{N}{\left(m.s^{-1}\right)^2}$
$\left[k\right]=\frac{N}{m^2.s^{-2}}$
$\left[k\right]=N.s^2.m^{-2}$

Remarque : l’unité Newton est $kg.m.s^{-2}$ (formule provenant de la deuxième loi de Newton :
$\Sigma\overrightarrow{F_{ext}}=m\overrightarrow{a}$ )

$\left[k\right]=Kg.m.s^{-2}.s^2.m^{-2}$
$\left[k\right]=Kg.m^{-1}$

Q10. Calculer la valeur f de la force de frottement en fin de chute. Comparer cette valeur à celle du poids du smartphone et commenter.

Graphiquement, sur la figure 4, en fin de chute, $v^2=25,0\ m^2.s^{-2}$
$f=0,0555\times m\times v^2$
$f=0,0555\times182\times{10}^{-3}\times25$
$f=0,250\ N$

Calculons le poids du smartphone :
$P=m\times g$
$P=182\times{10}^{-3}\times9,81$
$P=1,79\ N$

Comparons les deux forces :
$\frac{P}{f}=\frac{1,79}{0,250}=7,16$

Le poids est environs 7 fois plus grand que la force de frottement.

En fin de chute, la force de frottement est plus faible que le poids mais cependant elle n’est pas négligeable.